浙教版九年级上册第3章 圆的基本性质3.7 正多边形课文内容课件ppt

这是一份浙教版九年级上册第3章 圆的基本性质3.7 正多边形课文内容课件ppt，共28页。PPT课件主要包含了知识点，正多边形，正三角形，正方形，正五边形，正六边形，正八边形，正多边形的性质，九边形，正多边形及其外接圆等内容，欢迎下载使用。

了解正多边形和圆的有关概念；理解并掌握正多边形半径、中心角、弦心距、边长之间的关系，会应用多边形和圆的有关知识解决实际问题．
这个美丽图案的主体部分由一些多边形构成.你发现这些多边形有什么特别之处吗？
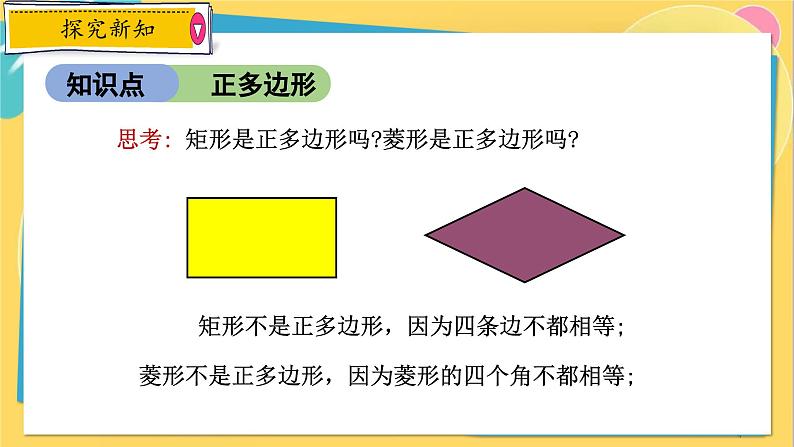
思考: 矩形是正多边形吗?菱形是正多边形吗?
矩形不是正多边形，因为四条边不都相等;
菱形不是正多边形，因为菱形的四个角不都相等;
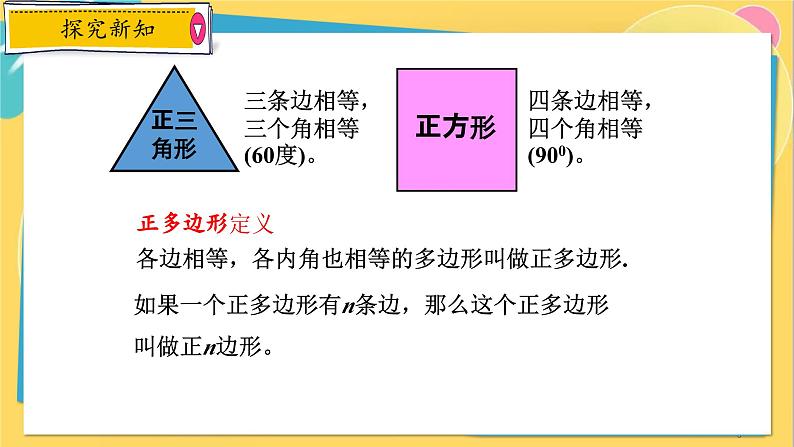
正多边形定义各边相等，各内角也相等的多边形叫做正多边形.
三条边相等，三个角相等(60度)。
四条边相等，四个角相等(900)。
如果一个正多边形有n条边，那么这个正多边形叫做正n边形。
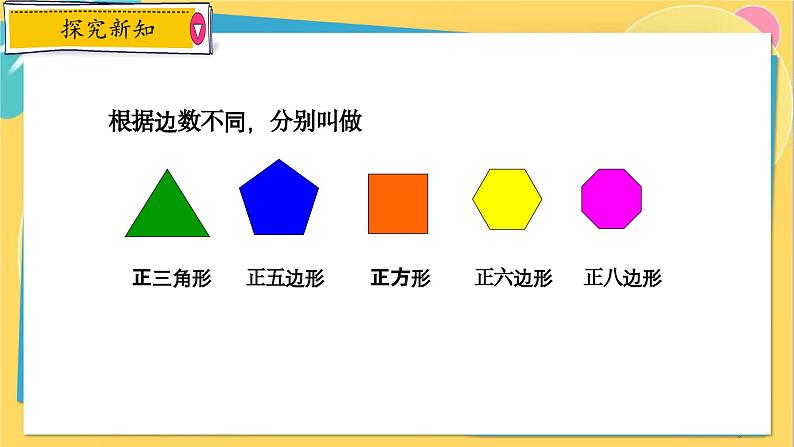
根据边数不同，分别叫做
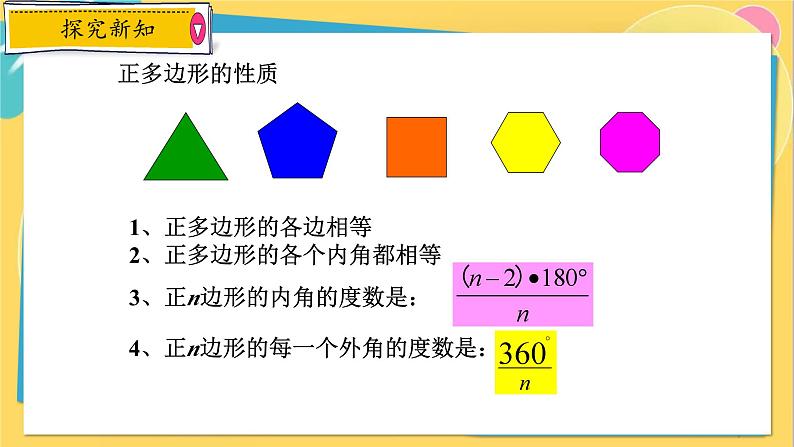
1、正多边形的各边相等2、正多边形的各个内角都相等
3、正n边形的内角的度数是：
4、正n边形的每一个外角的度数是：
已知一个正多边形的内角为176.4°，这个正多边形是几边形？有没有内角为100°的正多边形？
1、求正七边形的内角的度数。2、已知一个正多边形的内角140°，它是几边形？
如图，已知正三角形，用直尺和圆规作它的外接圆.
【分析】因为正三角形的外接圆经过正三角形的每一个顶点，则外接圆的圆心到每个顶点的距离相等，故外接圆的圆心在三角形任两条边的垂直平分线的交点上，半径为圆心到正三角形任一顶点的距离.
解：所求作正三角形的外接圆如图所示（作法步骤略）.
说一说，怎样作一个已知正方形的外接圆呢？
对于任意一个正三角形和正方形都能作出它的外接圆.我们把经过一个正多边形的各个顶点的圆叫做这个正多边形的外接圆，这个正多边形也就叫做圆内接正多边形.
任何一个正多边形都有一个外接圆。
…这样就得到圆周的n个等分点，顺次连结这n个点，就得到该圆的圆内接正n边形.
已知⊙O ，你能设计一种画该圆的圆内接正n边形的方法吗？
如图，已知⊙O，用直尺和圆规作⊙O的内接正六边形.
【分析】如图，设AB是⊙O的内接正六边形的一条边，连结OA，OB，则∠AOB=60°，所以△AOB为等边三角形，AB与⊙O的半径相等.因此，只要以⊙O的半径为半径，从⊙O上任取一点开始，依次在⊙O上截取五次，就把⊙O六等分.也就是说，依次连结这些分点，就得到所要求作的⊙O的内接正六边形.
正三角形是轴对称图形吗？如果是，有几条对称轴？正四边形、正五边形、正六边形呢？由此你能猜测正n边形有几条对称轴吗？
正三角形是中心对称图形吗？正四边形、正五边形、正六边形呢？由此你能猜测正n边形是否是中心对称图形吗？
2. 边数是偶数的正多边形还是中心对称图形。
正多边形的对称性1、正多边形都是轴对称图形，一个正n边形共有n条对称轴，每条对称轴都通过n边形的中心。
已知正六边形ABCDEF (如图).(1)用直尺和圆规作它的外接圆.(2)求证：CF是它的外接圆的直径.
解：所求作正六边形的外接圆如图所示，(作法步骤略).
一个正多边形的内角为144°，则它的边数为(　　)A．8 B．9 C．10 D．11
【2023·上海】如果一个正多边形的中心角是20°，那么这个正多边形的边数为________．
【2023·重庆】如图，在正五边形ABCDE中，连结AC，则∠BAC的度数为________．