初中数学浙教版九年级上册3.8 弧长及扇形的面积教案配套ppt课件

这是一份初中数学浙教版九年级上册3.8 弧长及扇形的面积教案配套ppt课件，共23页。PPT课件主要包含了知识点，扇形的概念，扇形的面积公式，πR2，做一做，πcm2，6cm2，割补法求面积，弓形面积公式等内容，欢迎下载使用。

1．理解扇形面积公式，并会计算扇形的面积．2．经历探索扇形面积计算公式的过程，感受转化、类比的数学思想，培养学生的探索能力．3．通过用扇形面积公式解决实际问题，让学生体验数学与人类生活的密切联系．
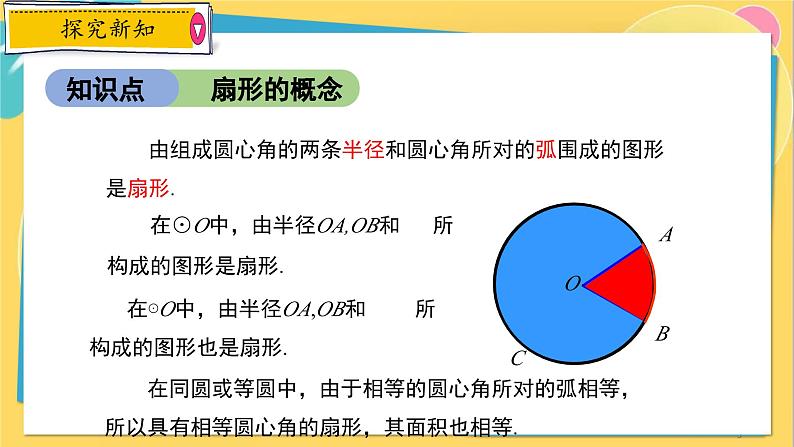
由组成圆心角的两条半径和圆心角所对的弧围成的图形是扇形.
　　在同圆或等圆中，由于相等的圆心角所对的弧相等，所以具有相等圆心角的扇形，其面积也相等.
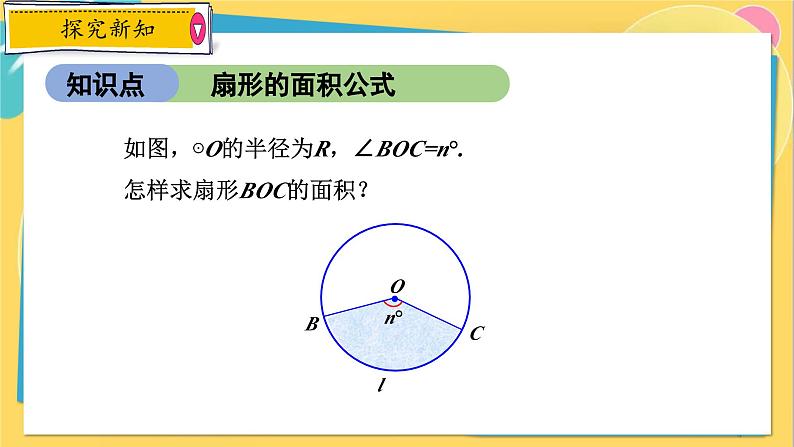
如图，⊙O的半径为R，∠BOC=n°.怎样求扇形BOC的面积？
n°的圆心角对应的扇形面积为__________.
如果圆的半径为R，则圆的面积为_______，
1°的圆心角对应的扇形面积为__________，
注意： ①公式中n的意义．n表示1°圆心角的倍数，它是不带单位的；②公式要理解记忆（即按照上面推导过程记忆）.
思考：扇形的弧长公式与面积公式有联系吗？
如果扇形的半径为R，圆心角为n°，扇形的弧长为l，那么扇形面积S的计算公式为：
已知圆的半径为6 cm，求下列各扇形的面积.（1）圆心角为90°的扇形面积__________;（2）圆心角为120°的扇形面积__________;（3）圆心角为240°的扇形面积__________;（4）弧长为7.2 cm的扇形面积__________;
如图，有一把折扇和一把团扇.已知折扇的骨柄与团扇的直径一样长，折扇扇面的宽度是骨柄长的一半，折扇张开的角度为120 °，问哪一把扇子扇面的面积大？
在扇形公式中，存在l、R、n、S四个量，我们只要知道其中两个就可以求得另外两个.
我国著名的引滦工程的主干线输水管的直径为2.5m，设计流量为12.73m³/s.如果水管截面中水面面积如图所示，其中∠AOB＝45°，那么水的流速应达到每秒多少米(精确到0.01m/s)？
【分析】由图，不难发现截面中有水部分（阴影部分）的面积是圆的面积与空隙部分（弓形）面积之差.因此根据水的流量、截面中水面面积与流速的关系，即可求得水的流速.
S弓形=S扇形-S三角形
弓形的面积=扇形的面积±三角形的面积
S弓形=S扇形+S三角形
求不规则图形面积的常用策略
(1)通过“割”“补”“拼”“凑”等方法将不规则图形的面积转化为几个规则图形面积的和或差的形式.
(2)通过等积代换的方法将不规则图形的面积转化成规则图形的面积.
已知扇形的半径为3，圆心角为120°，则扇形的面积是(　　)A．6π B．3π C．2π D．π
【2023·杭州十五中期末】若扇形的半径是12 cm，弧长是20 π cm，则扇形的面积为(　　)A．120π cm2 B．9π cm2C．6π cm2 D．3π cm2
【2023·菏泽】如图，正八边形ABCDEFGH的边长为4，以顶点A为圆心，AB的长为半径画圆，则阴影部分的面积为________(结果保留π)．