2024河南中考数学微专题复习 解决kAP+BP(k≠1)的线段最值问题 课件

这是一份2024河南中考数学微专题复习 解决kAP+BP(k≠1)的线段最值问题 课件，共14页。PPT课件主要包含了第1题图，第1题解图，第2题图，第3题图，第4题图，第4题解图，第5题图等内容，欢迎下载使用。

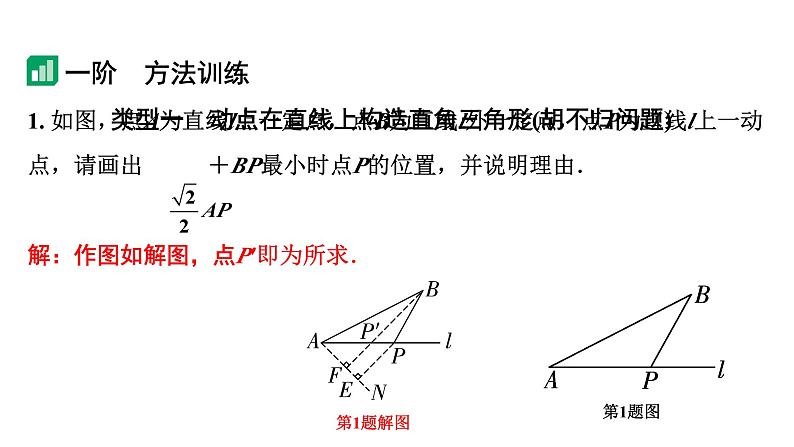
1. 如图，点A为直线l上一定点，点B为直线l外一定点，点P为直线l上一动点，请画出 ＋BP最小时点P的位置，并说明理由．
解：作图如解图，点P′即为所求．
类型一　动点在直线上构造直角三角形(胡不归问题)
过点B作BF⊥AN于点F，交直线l于点P′，当点P与点P′重合时， AP＋BP的值最小，∴点P′的位置即为所求．
理由如下：以点A为顶点作∠NAP，使sin∠NAP＝ ，过点P作垂线构造Rt△APE，∴ AP＝PE，∴ AP＋BP＝PE＋BP，
2. 如图，在▱ABCD中，∠DAB＝60°，AB＝8，点P为边CD上一动点，则PB＋ 的最小值为________．
3. 如图，在边长为4的等边△ABC中，BD⊥AC于点D，点E是BD上一点，则CE＋ 的最小值为________．
胡不归问题：构造直角三角形，利用“垂线段最短”求解；具体步骤：一找：找带有系数k的线段AP；二构造：构造以线段AP为斜边的直角三角形：①以定点A为顶点作∠NAP，使sin∠NAP＝k；②过动点P作AN的垂线，构造Rt△APE；三转化：化折为直，将kAP转化为PE；四求解：使得kAP＋BP＝PE＋BP，利用“垂线段最短”转化为求BF的长．
【温馨提示】①当AP＋kBP中系数k大于1时，考虑提取k值转化为k ，这样就转化为标准模型了．②k＝ →构造30°直角三角形；k＝ →构造等腰直角三角形；k＝ →构造60°直角三角形．
4. 如图，点P是半径为r的⊙O上的一个动点，点A，B为⊙O外的定点，且r＝ ，请画出 最小时点P的位置，并说明理由．
解：作图如解图，点P′即为所求，理由如下：
在线段OA上截取OC，使得OC＝ .连接OP，PC，BC交⊙O于点P′，∵点P在⊙O上，∴OP＝r，
类型二　动点在圆上构造相似三角形(阿氏圆问题)
∵r＝ ，∴ ＝ ＝ ，又∵∠COP＝∠POA，∴△COP∽△POA，∴ ＝ ＝ ＝ ，∴PC＝ ，∴ ＋BP＝PC＋BP，∴当B，P，C三点共线时， ＋BP的值最小，∴点P′位置即为所求．
5. 如图，在Rt△ABC中，∠ACB＝90°，CB＝4，CA＝6，⊙C的半径为2，点P为圆上一动点，连接AP，BP，则 的最小值为________．
阿氏圆问题：构造相似三角形，利用“两点之间线段最短”求解；具体步骤：一找：找带有系数k的线段AP；二构：在线段OA上取一点C，构造△PCO∽△APO；①在线段OA上截取OC，使OC＝k·r；②连接PC，OP，证明△PCO∽△APO；三转化：通过相似三角形的对应边成比例，将kPA转化为PC；四求解：使得kAP＋BP＝PC＋BP，利用“两点之间线段最短”转化为求BC的长．
1. 如图，正方形AOBC的边长为9，⊙O的半径为3，点P是⊙O上的一个动点，则 的最小值为________．
2. 如图，四边形ABCD为菱形，∠B＝60°，AB＝4，点E为AD上的定点，且AE＜ED，点F为AC上的动点，则 的最小值为________．