2024河南中考数学专题复习第六章 第四节 圆的实际应用 课件

这是一份2024河南中考数学专题复习第六章 第四节 圆的实际应用 课件，共21页。PPT课件主要包含了第1题图，第2题图，OC⊥CD，OB⊥AB，AB＝75cm，关键句翻译，第3题图，OP＝OB＝5，第4题图，AB＝BO＝CO等内容，欢迎下载使用。

1. (2023河南定心卷)停车楔(如图①)是一种固定汽车轮胎的装置，在大型货车于坡道停车时，放停车楔的作用尤为重要．如图②是轮胎和停车楔的示意图，当车停于水平地面上时，将停车楔B－ 置于轮胎⊙O后方即可防止车辆倒退，此时 紧贴轮胎，①边AB与地面重合且与轮胎⊙O相切于点A．为了更好地研究这个停车楔与轮胎⊙O的关系，小明在示意图②上，连接CO并延长交⊙O于点D，连接AD后发现AD∥BC.(1)求证：∠D＋∠B＝90°；
【关键句缩句】对①缩句：AB与圆O相切于点A.关联知识点：遇到切点，连接圆心，得垂直．结论：连接OA，可得OA⊥AB.
(1)证明：如图，连接OA，AC，
∵AB是⊙O的切线，∴∠OAB＝90°，∵CD为⊙O的直径，∴∠CAD＝90°，∴∠DAO＋∠OAC＝∠BAC＋∠OAC，∴∠DAO＝∠BAC，∵OD＝OA，∴∠D＝∠DAO，∴∠BAC＝∠D，(2分)∵BC∥AD，∴∠ACB＝∠CAD＝90°，∴∠BAC＋∠B＝180°－∠ACB＝90°，(3分)∵∠BAC＝∠D，∴∠D＋∠B＝90°；(4分)
(2)小明通过查阅资料从停车楔的规格了解到，此停车楔的高度为15 cm(点C到AB所在直线的距离)，支撑边BC与底边AB的夹角∠B＝60°，求轮胎的直径．
(2)解：如图，过点C作CE⊥AB于点E，则CE＝15，
由(1)得，∠B＋∠D＝90°，∠BAC＝∠D，∴∠BAC＝∠D＝90°－∠B＝90°－60°＝30°，∴∠AOC＝2∠D＝60°，∵OA＝OC，∴△OAC是等边三角形，(6分)，∴AC＝OA＝OC，
∵在Rt△ACE中，CE＝15，∠CAE＝30°，∴AC＝ ＝ ＝30，∴CD＝2OC＝2AC＝60 cm，∴轮胎的直径为60 cm.(9分)
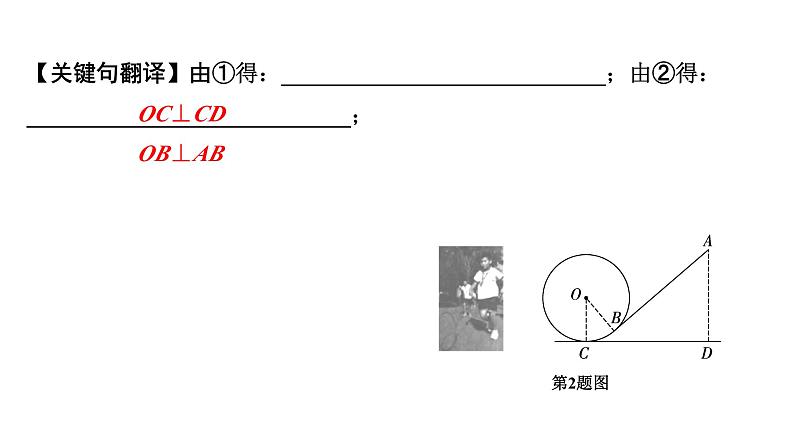
2. (2022河南22题10分)为弘扬民族传统体育文化，某校将传统游戏“滚铁环”列入了校运动会的比赛项目，滚铁环器材由铁环和推杆组成．小明对滚铁环的启动阶段进行了研究，如图，滚铁环时，①铁环⊙O与水平地面相切于点C，推杆AB与铅垂线AD的夹角为∠BAD，点O，A，B，C，D在同一平面内．②当推杆AB与铁环⊙O相切于点B时，手上的力量通过切点B传递到铁环上，会有较好的启动效果．(1)求证： ∠BOC＋∠BAD＝90°；
【关键句翻译】由①得：____________________________；由②得：____________________________；
(1)证明：如图，过点B作BN∥AD，
∴∠NBA＝∠BAD.∵CD与⊙O相切于点C，∴∠OCD＝90°.∵AD⊥CD，∴∠ADC＝90°，∴AD∥OC，∴BN∥OC，∴∠BOC＝∠NBO，(2分)∵AB与⊙O相切于点B，OB为半径，∴∠OBA＝90°，∴∠NBO＋∠NBA＝90°，∴∠BOC＋∠BAD＝90°；(4分)
(2)实践中发现，切点B只有在铁环上一定区域内时，才能保证铁环平稳启动．图中点B是该区域内最低位置，此时点A距地面的距离AD最小，测得cs∠BAD＝ .已知铁环③⊙O的半径为25cm，④推杆AB的长为75cm，求此时AD的长．
由③得：____________________；由④得：____________________．
OC＝OB＝25 cm
(2)解：如图，过点B作EF∥CD，分别交AD，OC于点E，F，
在Rt△OBF中，∵OB＝25，∴BF＝15，∴OF＝20.∵OC＝25，∴CF＝5.(9分)∵∠OCD＝∠ADC＝∠CFE＝90°，∴四边形CDEF为矩形，∴DE＝CF＝5，∴AD＝AE＋ED＝50 cm.(10分)
3. (2021河南20题9分)在古代，智慧的劳动人民已经会使用“石磨”，其原理为在磨盘的边缘连接一个固定长度的“连杆”，推动“连杆”带动磨盘转动，将粮食磨碎，物理学上称这种动力传输工具为“曲柄连杆机构”．小明受此启发设计了一个“双连杆机构”，设计图如图①，两个固定长度的“连杆”AP，BP的连接点P在⊙O上，当点P在⊙O上转动时，带动点A，B分别在射线OM，ON上滑动，OM⊥ON.①当AP与⊙O相切时，点B恰好落在⊙O上，如图②.请仅就图②的情形解答下列问题．(1)求证：∠PAO＝2∠PBO；
【关键句翻译】由①得：_____________________________________；由②得：_____________________________________．
连接OP，OP⊥AP，且点B为⊙O上一点
(1)证明：如图，连接OP，(1分)
∵AP是⊙O的切线，∴OP⊥AP，∴∠OPA＝90°，∴∠PAO＋∠POA＝90°.∵OA⊥OB，∴∠POA＋∠1＝90°，∴∠PAO＝∠1.(3分)∵OP＝OB，∴∠OPB＝∠PBO，∴∠1＝2∠PBO，∴∠PAO＝2∠PBO；(5分)
(2)若②⊙O的半径为5，AP＝ ，求BP的长．
(2)解：如图，过点P作PC⊥NO，垂足为点C.(6分)
4.我们学习过利用尺规作图平分一个任意角，而“利用尺规作图三等分一个任意角”曾是数学史上一大难题，之后被数学家证明是不可能完成的，人们根据实际需要，发明了一种简易操作工具——三分角器．图①是它的示意图，其中①AB与半圆O的直径BC在同一直线上，且②AB的长度与半圆的半径相等；③DB与AC垂直于点B，DB足够长．使用方法如图②所示，若要把∠MEN三等分，只需适当放置三分角器，使④DB经过∠MEN的顶点E，点A落在边EM上，⑤半圆O与另一边EN恰好相切，切点为F，则EB，EO就把∠MEN三等分了．
为了说明这一方法的正确性，需要对其进行证明．如下给出了不完整的“已知”和“求证”，请补充完整，并写出“证明”过程．已知：如图②，点A，B，O，C在同一直线上，EB⊥AC，垂足为点B，________．求证：________．
【关键句翻译】由①得：______________________；由②得：______________________；由③得：______________________；由④得：______________________；【关键句缩句】缩句：对⑤缩句：_______________________________________________；关联知识点：___________________________________________________；结论：_______________________________.
A，B，O，C四点共线
点E在BD上，点A在EM上
EN与半圆O相切于点F
遇到切点，连接圆心，得垂直
连接OF，可得OF⊥EN
解：已知：如图②，点A，B，O，C在同一直线上，EB⊥AC，垂足为点B，AB＝OB，EN切半圆O于点F.(2分)求证：∠1＝∠2＝∠3.(3分)证明：如图，连接OF.(4分)
∵EB⊥AC，∴∠ABE＝∠OBE＝90°.又∵AB＝OB，EB＝EB，∴△ABE≌△OBE，∴∠1＝∠2.(6分)∵EN切半圆O于点F，∴OF⊥EF.又∵OB⊥BE且OF＝OB，∴EO平分∠BEF，∴∠3＝∠2，∴∠1＝∠2＝∠3.(9分)