2024河南中考数学全国真题分类卷 第十一讲 二次函数与几何图形综合题(含答案)

这是一份2024河南中考数学全国真题分类卷 第十一讲 二次函数与几何图形综合题(含答案)，共15页。试卷主要包含了 如图，已知抛物线等内容，欢迎下载使用。
1. (2023常德)如图，已知抛物线过点O(0，0)，A(5，5)，且它的对称轴为x＝2.
(1)求此抛物线的解析式；
(2)若点B是抛物线对称轴上的一点，且点B在第一象限，当△OAB的面积为15时，求B的坐标；
(3)在(2)的条件下，P是抛物线上的动点，当PA－PB的值最大时，求P的坐标以及PA－PB的最大值．
第1题图
类型二 面积问题
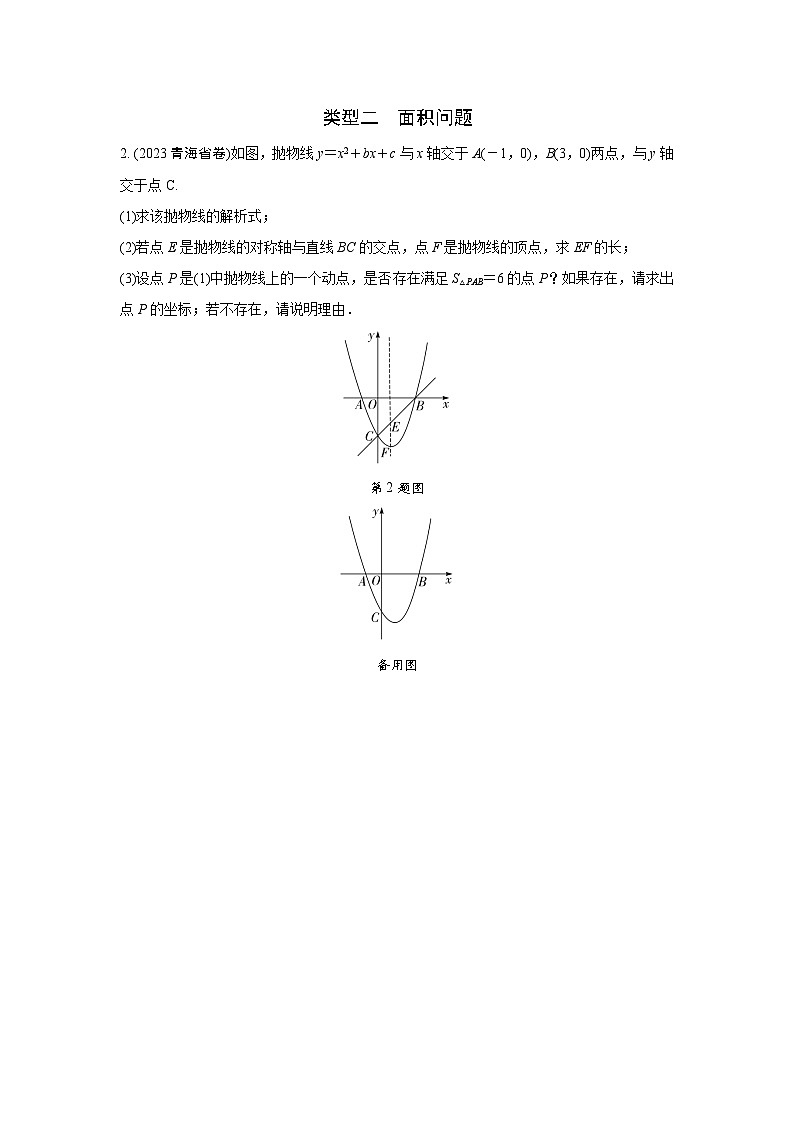
2. (2023青海省卷)如图，抛物线y＝x2＋bx＋c与x轴交于A(－1，0)，B(3，0)两点，与y轴交于点C.
(1)求该抛物线的解析式；
(2)若点E是抛物线的对称轴与直线BC的交点，点F是抛物线的顶点，求EF的长；
(3)设点P是(1)中抛物线上的一个动点，是否存在满足S△PAB＝6的点P？如果存在，请求出点P的坐标；若不存在，请说明理由．
第2题图
备用图
类型三 角度问题
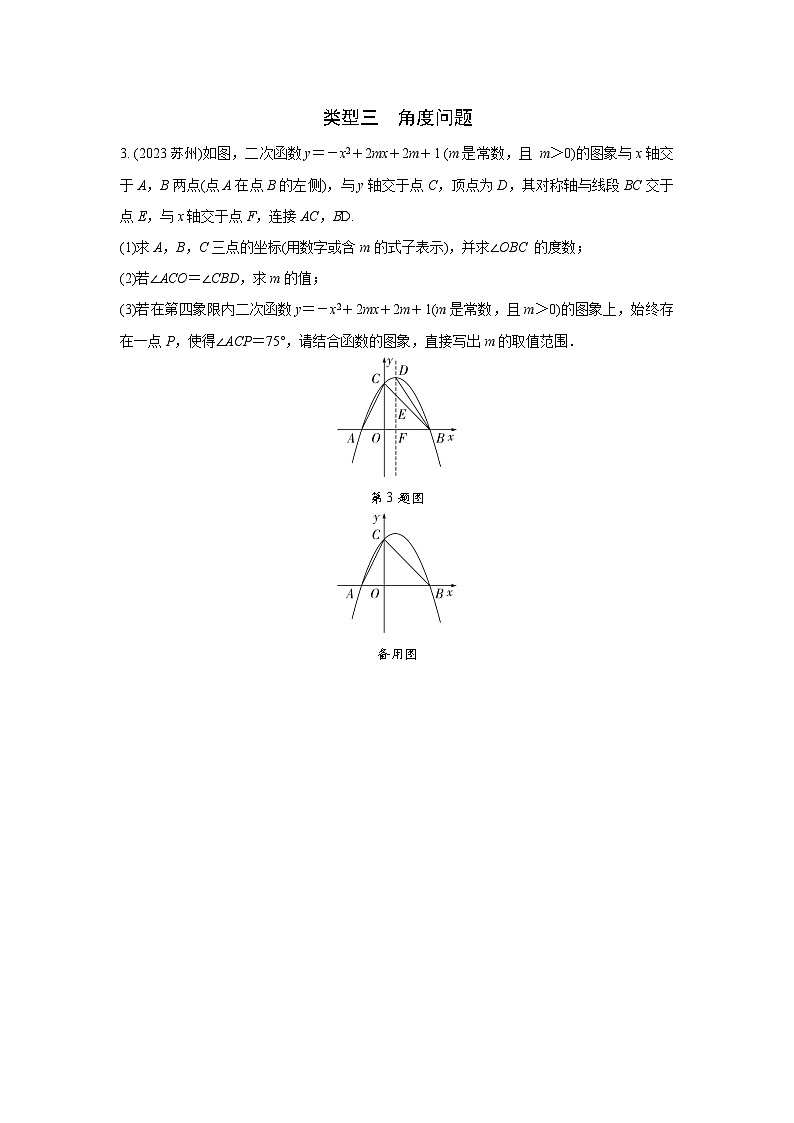
3. (2023苏州)如图，二次函数y＝－x2＋2mx＋2m＋1 (m是常数，且 m＞0)的图象与x轴交于A，B两点(点A在点B的左侧)，与y轴交于点C，顶点为D，其对称轴与线段BC交于点E，与x轴交于点F，连接AC，BD.
(1)求A，B，C三点的坐标(用数字或含m的式子表示)，并求∠OBC 的度数；
(2)若∠ACO＝∠CBD，求m的值；
(3)若在第四象限内二次函数y＝－x2＋2mx＋2m＋1(m是常数，且m＞0)的图象上，始终存在一点P，使得∠ACP＝75°，请结合函数的图象，直接写出m的取值范围．
第3题图
备用图
类型四 特殊三角形判定问题
4. (2023滨州)如图，在平面直角坐标系中，抛物线y＝x2－2x－3与x轴相交于点A，B(点A在点B的左侧)，与y轴相交于点C，连接AC，BC.
(1)求线段AC的长；
(2)若点P为该抛物线对称轴上的一个动点，当PA＝PC时，求点P的坐标；
(3)若点M为该抛物线上的一个动点，当△BCM为直角三角形时，求点M的坐标．
第4题图
备用图
类型五 特殊四边形判定问题
5. (2023毕节)如图，在平面直角坐标系中，抛物线y＝－x2＋bx＋c与x轴交于A，B两点，与y轴交于点C，顶点为D(2，1)，抛物线的对称轴交直线BC于点E.
(1)求抛物线y＝－x2＋bx＋c的表达式；
(2)把上述抛物线沿它的对称轴向下平移，平移的距离为h(h>0)，在平移过程中，该抛物线与直线BC始终有交点，求h的最大值；
(3)M是(1)中抛物线上一点，N是直线BC上一点．是否存在以点D，E，M，N为顶点的四边形是平行四边形？若存在，求出点N的坐标；若不存在，请说明理由．
第5题图
备用图
类型六 相似三角形判定问题
6. (2023玉林)如图，已知抛物线：y＝－2x2＋bx＋c与x轴交于点A，B(2，0)(A在B的左侧)，与y轴交于点C，对称轴是直线x＝ eq \f(1,2) ，P是第一象限内抛物线上的任一点．
(1)求抛物线的解析式；
(2)若点D为线段OC的中点，则△POD能否是等边三角形？请说明理由；
(3)过点P作x轴的垂线与线段BC交于点M，垂足为点H，若以P，M，C为顶点的三角形与△BMH相似，求点P的坐标．
第6题图
备用图
参考答案与解析
1. 解：(1)设抛物线的解析式为y＝a(x－2)2＋h，
把O(0，0)，A(5，5)代入，
得 eq \b\lc\{(\a\vs4\al\c1(4a＋h＝0,9a＋h＝5)) ，解得 eq \b\lc\{(\a\vs4\al\c1(a＝1,h＝－4)) ，
∴抛物线的解析式为y＝(x－2)2－4，即y＝x2－4x；
(2)如解图①，记OA与直线x＝2的交点为C，
设直线OA的解析式为y＝kx，则5＝5k，
解得k＝1，
∴直线OA的解析式为y＝x，
将x＝2代入得y＝2，∴C(2，2).
设B(2，m)，则BC＝|m－2|，
∴S△OAB＝ eq \f(1,2) BC·|xA|＝ eq \f(5,2) |m－2|，
∵△OAB的面积为15，
∴ eq \f(5,2) |m－2|＝15，
解得m＝8或m＝－4，
∵点B在第一象限内，
∴m＞0，∴m＝8，故B(2，8)；
图①
图②
第1题解图
(3)如解图②，连接PA，PB，AB，
∵PA－PB≤AB，
∴当P，B，A在同一直线上时，PA－PB取得最大值，最大值为AB的长，
∵A(5，5)，B(2，8)，
∴AB＝ eq \r(（2－5）2＋（8－5）2) ＝3 eq \r(2) ，
设直线AB的解析式为y＝px＋n(p≠0)，
将A(5，5)，B(2，8)分别代入，
得 eq \b\lc\{(\a\vs4\al\c1(5p＋n＝5,2p＋n＝8)) ，解得 eq \b\lc\{(\a\vs4\al\c1(p＝－1,n＝10)) ，
∴直线AB的解析式为y＝－x＋10，
联立 eq \b\lc\{(\a\vs4\al\c1(y＝－x＋10,y＝x2－4x)) ，
解得 eq \b\lc\{(\a\vs4\al\c1(x1＝5,y1＝5)) (舍去)， eq \b\lc\{(\a\vs4\al\c1(x2＝－2,y2＝12)) ，
∴P(－2，12)，
∴当PA－PB的值最大时，点P的坐标为(－2，12)，PA－PB的最大值为3 eq \r(2) .
2. 解：(1)∵抛物线y＝x2＋bx＋c与x轴交于A(－1，0)，B(3，0)两点，
∴ eq \b\lc\{(\a\vs4\al\c1(1－b＋c＝0,9＋3b＋c＝0)) ，解得 eq \b\lc\{(\a\vs4\al\c1(b＝－2,c＝－3)) ，
∴抛物线的解析式为y＝x2－2x－3；
(2)由(1)知，该抛物线的解析式为y＝x2－2x－3，则C(0，－3).
∵y＝x2－2x－3＝(x－1)2－4，
∴F(1，－4).
设直线BC的解析式为y＝kx－3(k≠0)，
把B(3，0)代入，得0＝3k－3，
解得k＝1，∴直线BC的解析式为y＝x－3.
当x＝1时，y＝－2，即E(1，－2)，
∴EF＝－2－(－4)＝2.即EF＝2；
(3)存在．理由如下：
设点P的坐标为(x，y)，
由题意，得S△PAB＝ eq \f(1,2) ×4×|y|＝6，
∴|y|＝3，∴y＝±3.
当y＝3时，x2－2x－3＝3，
解得x1＝1＋ eq \r(7) ，x2＝1－ eq \r(7) ，
∴P(1＋ eq \r(7) ，3)或P(1－ eq \r(7) ，3)；
当y＝－3时，x2－2x－3＝－3，
解得x3＝0，x4＝2，
∴P(0，－3)或P(2，－3).
综上所述，点P的坐标为(1＋ eq \r(7) ，3)或(1－ eq \r(7) ，3)或(0，－3)或(2，－3).
3. 解：(1)当y＝0时，－x2＋2mx＋2m＋1＝0，
解得x1＝－1，x2＝2m＋1，
∵点A在点B的左侧，且m＞0，
∴A(－1，0)，B(2m＋1，0)，
当x＝0时，y＝2m＋1.
∴C(0，2m＋1)，
∴OB＝OC＝2m＋1.
∵∠BOC＝90°，
∴∠OBC＝45°；
(2)如解图①，连接AE.
第3题解图①
∵y＝－x2＋2mx＋2m＋1＝－(x－m)2＋(m＋1)2，
∴D[m，(m＋1)2]，F(m，0)，
∴DF＝(m＋1)2，OF＝m，BF＝m＋1.
∵点A，B关于对称轴对称，
∴AE＝BE，
∴∠EAB＝∠OBC＝45°，
∴∠CEA＝90°，
∵∠ACO＝∠CBD，∠OCB＝∠OBC，
∴∠ACO＋∠OCB＝∠CBD＋∠OBC，即∠ACE＝∠DBF.
∵EF∥OC，
∴tan ∠ACE＝ eq \f(AE,CE) ＝ eq \f(BE,CE) ＝ eq \f(BF,OF) ＝ eq \f(m＋1,m) ，
∵∠DFB＝90°，
∴tan ∠DBF＝ eq \f(DF,BF) ＝ eq \f(（m＋1）2,m＋1) ＝m＋1.
∴ eq \f(m＋1,m) ＝m＋1，解得m＝±1.
∵m＞0，
∴m＝1；
【一题多解】如解图②，过点D作DH⊥BC于点H，
由上述可得DF＝(m＋1)2，BF＝EF＝m＋1.
∴DE＝m2＋m.
∵∠DEH＝∠BEF＝45°，
∴DH＝EH＝ eq \f(\r(2),2) DE＝ eq \f(\r(2),2) (m2＋m)，BE＝ eq \r(2) BF＝ eq \r(2) (m＋1)，
∴BH＝BE＋HE＝ eq \f(\r(2),2) (m2＋3m＋2).
∵∠ACO＝∠CBD，∠AOC＝∠BHD＝90°，
∴△AOC∽△DHB，
∴ eq \f(OA,OC) ＝ eq \f(HD,HB) ，
∴ eq \f(1,2m＋1) ＝ eq \f(\f(\r(2),2)（m2＋m）,\f(\r(2),2)（m2＋3m＋2）) ，即 eq \f(1,2m＋1) ＝ eq \f(m,m＋2) ，
解得m＝±1，
∵m＞0，
∴m＝1；
第3题解图②
(3)0＜m＜ eq \f(\r(3)－1,2) .
【解法提示】如解图③，连接PC，设PC与x轴交于点Q，当P在第四象限时，点Q总在点B的左侧，此时∠CQA＞∠CBA，即∠CQA＞45°.∵∠ACQ＝75°，∴∠CAO＜60°，∴2m＋1＜ eq \r(3) ，∴m＜ eq \f(\r(3)－1,2) ，∴0＜m＜ eq \f(\r(3)－1,2) .
第3题解图③
4. 解：(1)令y＝0，即x2－2x－3＝0，
解得x1＝－1，x2＝3，
∵点A在点B左侧，
∴A(－1，0)，B(3，0).
令x＝0，解得y＝－3，
∴C(0，－3)，
∴AO＝1，CO＝3，
∴AC＝ eq \r(AO2＋CO2) ＝ eq \r(10) ；
(2)如解图，过点C作对称轴的垂线，垂足为E，设对称轴交x轴于点D，
∵抛物线y＝x2－2x－3的对称轴为直线x＝1，
∴D(1，0).
∵点P在该抛物线的对称轴上，
∴设P(1，t).
∵A(－1，0)，C(0，－3)，
∴E(1，－3)，
∴AD＝2，DP＝－t，CE＝1，PE＝t＋3，
∴PA2＝AD2＋DP2＝22＋(－t)2＝4＋t2，PC2＝CE2＋PE2＝1＋(t＋3)2.
∵PA＝PC，即PA2＝PC2，
∴4＋t2 ＝1＋(t＋3)2，
解得t＝－1，
∴点P的坐标为(1，－1)；
第4题解图
(3)设M(m，m2－2m－3)，
∵B(3，0)，C(0，－3)，
∴BM2＝(m－3)2＋(m2－2m－3)2，BC2＝32＋32＝18，CM2＝m2＋(m2－2m)2.
当△BCM为直角三角形时，可分三种情况讨论：
①当∠BCM＝90°时，即CM2＋BC2＝BM2，
∴m2＋(m2－2m)2＋18＝(m－3)2＋(m2－2m－3)2，
解得m1＝0(舍去)，m2＝1，
∴M(1，－4)；
②当∠CBM＝90°时，即BM2＋BC2＝CM2，
∴(m－3)2＋(m2－2m－3)2＋18＝m2＋(m2－2m)2，
解得m3＝－2，m4＝3(舍去)，
∴M(－2，5)；
③当∠BMC＝90°时，即BM2＋CM2＝BC2，
∴(m－3)2＋(m2－2m－3)2＋m2＋(m2－2m)2＝18，
解得m5＝ eq \f(1＋\r(5),2) ，m6＝ eq \f(1－\r(5),2) ，m7＝0(舍去)，m8＝3(舍去)，
∴M( eq \f(1＋\r(5),2) ，－ eq \f(5＋\r(5),2) )或M( eq \f(1－\r(5),2) ，－ eq \f(5－\r(5),2) )；
综上所述，点M的坐标为(1，－4)或(－2，5)或( eq \f(1＋\r(5),2) ，－ eq \f(5＋\r(5),2) )或( eq \f(1－\r(5),2) ，－ eq \f(5－\r(5),2) ).
5. 解：(1)∵抛物线y＝－x2＋bx＋c的顶点坐标为D(2，1)，
∴抛物线的表达式为y＝－(x－2)2＋1＝－x2＋4x－3；
(2)由(1)知，抛物线的表达式为y＝－x2＋4x－3，
令x＝0，则y＝－3，
∴C(0，－3)，
令y＝0，则x＝1或x＝3，
∴A(1，0)，B(3，0)，
∴直线BC的表达式为y＝x－3.
设平移后的抛物线的表达式为y＝－(x－2)2＋1－h，
令－(x－2)2＋1－h＝x－3，整理得x2－3x＋h＝0，
∵该抛物线与直线BC始终有交点，
∴Δ＝9－4h≥0，
∴h≤ eq \f(9,4) ，
∴h的最大值为 eq \f(9,4) ；
(3)存在．理由如下：
由题意得，抛物线的对称轴为直线x＝2，
∴E(2，－1)，
∴DE＝2，
设M(m，－m2＋4m－3)，
若以点D，E，M，N为顶点的四边形是平行四边形，则分以下两种情况：
①当DE为边时，DE∥MN，DE＝MN，
则N(m，m－3)，
∴MN＝|－m2＋4m－3－(m－3)|＝|－m2＋3m|，
∴|－m2＋3m|＝2，解得m＝1或m＝2(舍去)或m＝ eq \f(3－\r(17),2) 或m＝ eq \f(3＋\r(17),2) .
∴点N的坐标为(1，－2)或( eq \f(3－\r(17),2) ， eq \f(－3－\r(17),2) )或( eq \f(3＋\r(17),2) ， eq \f(－3＋\r(17),2) )；
②当DE为对角线时，
设点N的坐标为t，
则N(t，t－3)，
∴ eq \b\lc\{(\a\vs4\al\c1(m＋t＝2＋2,－m2＋4m－3＋t－3＝1＋（－1）)) ，
解得 eq \b\lc\{(\a\vs4\al\c1(m＝1,t＝3)) 或 eq \b\lc\{(\a\vs4\al\c1(m＝2,t＝2)) (舍去)，
∴N(3，0).
综上所述，点N的坐标为(1，－2)或( eq \f(3－\r(17),2) ， eq \f(－3－\r(17),2) )或( eq \f(3＋\r(17),2) ， eq \f(－3＋\r(17),2) )或(3，0).
6. (1)解：∵抛物线的对称轴为直线x＝ eq \f(1,2) ，
∴－ eq \f(b,－2×2) ＝ eq \f(1,2) ，
∴b＝2，
把B(2，0)代入y＝－2x2＋2x＋c，得0＝－2×4＋4＋c，
解得c＝4，
∴抛物线的解析式为y＝－2x2＋2x＋4；
(2)△POD不能是等边三角形，理由如下：
当x＝0时，y＝4，
∴C(0，4)，OC＝4，
∵D为OC的中点，
∴D(0，2)，
若△POD为等边三角形，则点P的坐标应为( eq \r(3) ，1)，
把x＝ eq \r(3) 代入y＝－2x2＋2x＋4，得y＝2 eq \r(3) －2≠1，
∴此时点P不在抛物线上，
∴△POD不能是等边三角形；
(3)∵∠PMC＝∠BMH，
∴可分两种情况讨论如下：
①如解图①，若△BMH∽△CMP，则∠CPM＝∠BHM＝90°，即CP∥x轴，
∴点C和点P关于直线x＝ eq \f(1,2) 对称，
∵C(0，4)，∴P(1，4)；
②如解图②，若△BMH∽△PMC，则∠PCM＝∠BHM＝90°，过点C作CN⊥PH于点N，则四边形OCNH是矩形，
∴∠OCN＝90°，
∴∠OCB＋∠BCN＝∠NCP＋∠BCN，
∴∠OCB＝∠NCP，
∵∠BOC＝∠PNC，
∴△BOC∽△PNC，
∴ eq \f(PN,CN) ＝ eq \f(BO,CO) ＝ eq \f(1,2) ，
设PN＝m，则CN＝2m，
∵NH＝OC＝4，∴PH＝4＋m，
∴P(2m，4＋m)，代入y＝－2x2＋2x＋4，
得4＋m＝－2×(2m)2＋2×2m＋4，
解得m1＝0(舍去)，m2＝ eq \f(3,8) ，
∴P( eq \f(3,4) ， eq \f(35,8) ).
综上所述，点P的坐标为(1，4)或( eq \f(3,4) ， eq \f(35,8) ).
第6题解图