江苏省苏州市吴江、吴中、相城、新区四区2023-2024学年七年级下学期期中考试数学试卷(含答案)

这是一份江苏省苏州市吴江、吴中、相城、新区四区2023-2024学年七年级下学期期中考试数学试卷(含答案)，共10页。试卷主要包含了04，已知，，则________等内容，欢迎下载使用。
本卷由选择题、填空题和解答题组成，共27题，满分130分，调研时间120分钟.
注意事项：
1.答题前，考生务必将学校、班级、姓名、调研号等信息填写在答题卡相应的位置上.
2.答选择题必须用2B铅笔把答题卡上对应题目的答案标号涂黑，如需改动，请用橡皮擦干净后，再选涂其他答案；答非选择题必须用0.5毫米黑色墨水签字笔写在答题卡指定的位置上，不在答题区域内的答案一律无效；如需作图，先用2B铅笔画出图形，再用0.5毫米黑色墨水签字笔描黑，不得用其他笔答题.
3.考生答题必须答在答题卡相应的位置上，答在试卷和草稿纸上一律无效.
一、选择题（本大题共8小题，每小题3分，共24分.在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将答案填涂在答题卡相应位置上.）
1.下列长度（单位：）的三根小木棒，能搭成为三角形的是（ ）
A.3，4，8B.5，6，11C.5，6，10D.8，8，16
2.已知正多边形的一个外角等于，则该正多边形的边数为（ ）
A.3B.4C.5D.6
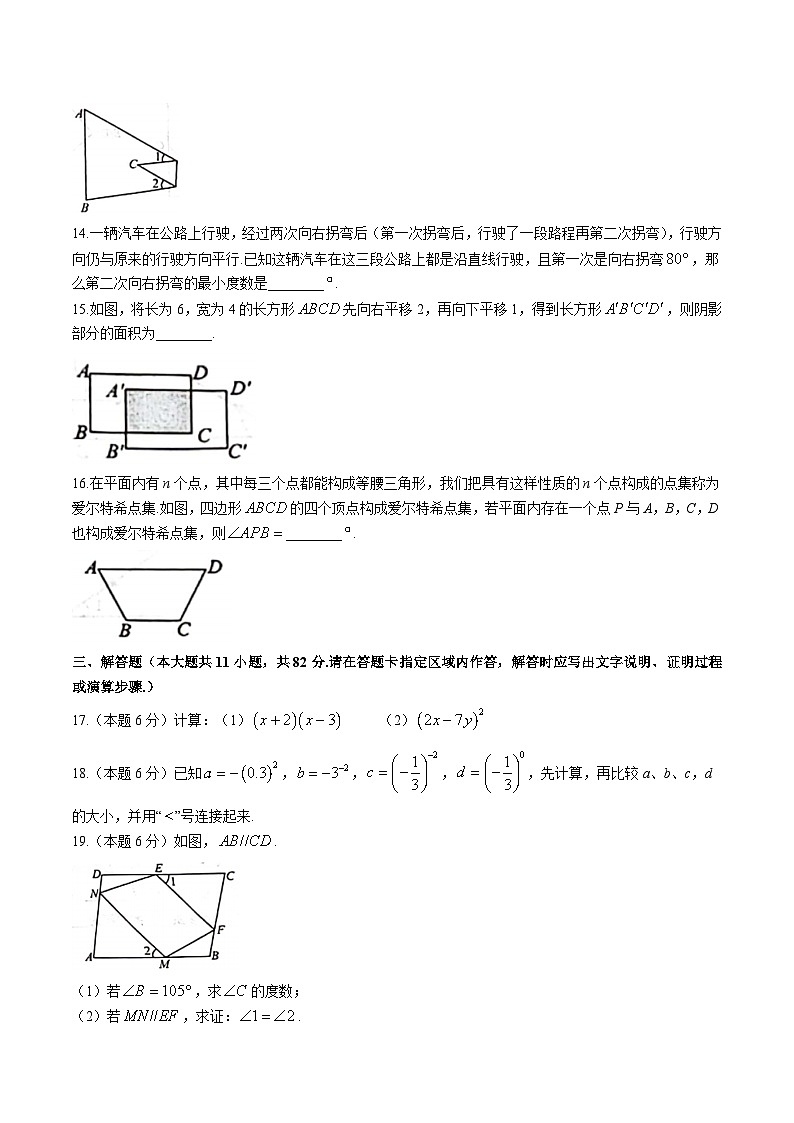
3.如图，在一个弯形管道中，测得，后，就可以知道管道，其依据的定理是（ ）
A.同位角相等，两直线平行B.内错角相等，两直线平行
C.同旁内角互补，两直线平行D.平行于同一条直线的两直线平行
4.计算的结果正确的是（ ）
A.B.C.D.
5.如图，木工师傅在做完门框后，为防止变形常常像图中所示那样钉上两条斜拉的木板条（即图中的和）.这样做的依据是（ ）
A.矩形的对称性B.三角形的稳定性C.两点之间线段最短D.垂线段最短
6.如图，直线，将一块含的直角三角板按如图方式放置，其中A，C两点分别落在直线a，b上，若，则的度数为（ ）
A.B.C.D.
7.如图，将沿方向平移到，若A，D之间的距离为2，，则等于（ ）
A.6B.7C.8D.9
8.如图，在数学兴趣活动中，小吴将两根长度相同的铁丝，分别做成甲、乙两个长方形，面积分别为，，则的值是（ ）
A.B.C.27D.3
二、填空题（本大题共8小题，每小题3分，共24分.不需写出解答过程，请把答案直接填写在答题卡相应位置上.）
9.已知，，则________.
10.如图，直线a，b被直线c所截，添加一个条件________，使.
11.分解因式：________.
12.如果，那么m的值为________
13.如图，在三角形纸片中，，，将纸片的一角折叠，使点C落在内，若，则_________.
14.一辆汽车在公路上行驶，经过两次向右拐弯后（第一次拐弯后，行驶了一段路程再第二次拐弯），行驶方向仍与原来的行驶方向平行.已知这辆汽车在这三段公路上都是沿直线行驶，且第一次是向右拐弯，那么第二次向右拐弯的最小度数是________.
15.如图，将长为6，宽为4的长方形先向右平移2，再向下平移1，得到长方形，则阴影部分的面积为________.
16.在平面内有n个点，其中每三个点都能构成等腰三角形，我们把具有这样性质的n个点构成的点集称为爱尔特希点集.如图，四边形的四个顶点构成爱尔特希点集，若平面内存在一个点P与A，B，C，D也构成爱尔特希点集，则________.
三、解答题（本大题共11小题，共82分.请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤.）
17.（本题6分）计算：（1）（2）
18.（本题6分）已知，，，，先计算，再比较a、b、c，d的大小，并用“”号连接起来.
19.（本题6分）如图，.
（1）若，求的度数；
（2）若，求证：.
20.（本题6分）把下列各式因式分解：
（1）；
（2）.
21.（本题6分）规定.
（1）求；
（2）若，求x的值.
22.（本题6分）如图，点E在上，点F在上，、分别交于点G、H，已知，.
（1）与平行吗?请说明理由；
（2）若，且，求的度数。
23.（本题8分）如图，在由小正方形组成的网格中，利用平移的知识完成下列作图.
（1）过D作，且；
（2）的面积为________；
（3）四边形的面积为________.
24.（本题8分）如图1，把一张长方形纸片沿折叠后与的交点为G.，
图1图2
（1）求，的度数.
（2）再沿折叠成如图2，求图2中的的度数.
25.（本题10分）
（1）知识探究：，，，……，上述括号按顺序填写为_____、______、_____；
（2）发现规律：试写出第n个等式，并证明此等式成立；
（3）拓展应用：计算.
26.（本题10分）实验证明，平面镜反射光线的规律是：射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.如图1，一束光线m射到平面镜a上，被a反射后的光线为n，则入射光线m、反射光线n与平面镜a所夹的锐角.
图1图2 图3
（1）利用这个规律人们制作了潜望镜，图2是潜望镜工作原理示意图，、是平行放置的两面平面镜.已知光线沿直线m进入潜望镜，最后沿直线n射出，求证.
（2）显然，改变两面平面镜、之间的位置关系，经过两次反射后，入射光线m与反射光线n之间的位置关系会随之改变，如图3，一束光线m射到平面镜上，被反射到平面镜上，又被反射.若被反射出的光线n和光线m平行，且，则________，______.
（3）请你猜想：图3中，当两平面镜、的夹角______时，可以使任何入射光线m经过平面镜、的两次反射后，与反射光线n平行，请说明理由.
27.（本题10分）阅读材料：的末尾数字是3，的末尾数字是9，的末尾数字是7，的末尾数字是1，的末尾数字是3，……，观察规律：
的末尾数字是1，
的末尾数字是1，
的末尾数字是3，
同理可知，的末尾数字是9，的末尾数字是7.
解答下列问题：
（1）的末尾数字是_______，的末尾数字是_______；
（2）求的末尾数字；
（3）求证：能被5整除.
数学参考答案
2024.04
一、选择题：（每小题3分，共24分）
二、填空题（每小题3分，共24分）
9.10；10.（答案不唯一）11.；
12.213.度；14.；15.12；
16.或
三、解答题（共11小题，共82分）
17.（本题满分6分）
解：（1）
（2）
18.（本题满分6分）
解：，，，
19.（本题满分6分）
（1）解：，，
，；
（2）证明：连接，
， ，
，，
，，.
20.（本题满分6分）
解：（1）原式.
（2）原式.
21.（本题满分6分）
解：（1）因为，所以；
（2）因为，所以，则，解得.
22.（本题满分6分）
（1）解：，理由如下：
，，，，
；
（2）解：，，，
，即，，
.
23.（本题满分8分）（1）解：所作直线、线段，如下图所示：
（2）解：的面积为：；
故答案为：5.
（3）解：如图所示，F在D点下方.
四边形的面积为：；
四边形的面积为11.
故答案为：11.
24.（本题满分8分）解：（1）由折叠的性质可得，，
，，
，，
，；
（2），，
，，
.
25.（本题满分10分）
解：（1）0，1，2（错一个全错）
（2）
，即，
.
（3）
.
26.（本题满分10分）
解：（1）证明：（已知），（①两直线平行，内错角相等），
，（已知），（②等量代换），
，即：，
（③内错角相等，两直线平行）
（2）解：由题意得，，，，
，，，
，
，
故答案为：96，90.
（3）当时，可以使任何入射光线m经过平面镜、的两次反射后，与反射光线n平行，理由如下：
解：由（1）得，，，
，，
，，
，，
，
故答案为：.
27.（本题满分10分）
（1）解：，的末尾数字为3；
的末尾数字是4，的末尾数字是6，的末尾数字是4，…
的末尾数字是4，的末尾数字是6，
的末尾数字是6；
故答案为：3，6；
（2）解：，
的末尾数字是6，的末尾数字是6；
（3）证明：的末尾数字是2，的末尾数字是4，的末尾数字是8，的末尾数字是6，的末尾数字是2，…
的末尾数字是2，的末尾数字是4，的末尾数字是8，的末尾数字是6，
的末尾数字为6；
同理可得：
的末尾数字7，的末尾数字9，的末尾数字3，的末尾数字1；
的末尾数字9，的末尾数字是5，
能被5整除.题号
1
2
3
4
5
6
7
8
答案
C
D
C
A
B
C
B
D