高一数学上学期期中期末重点突破(人教A版必修第一册)21利用诱导公式进行化简和求值(原卷版+解析)

这是一份高一数学上学期期中期末重点突破(人教A版必修第一册)21利用诱导公式进行化简和求值(原卷版+解析)，共24页。试卷主要包含了诱导公式的两个应用，常见的互余关系有与，与，与等；等内容，欢迎下载使用。


1.诱导公式的两个应用
①求值：负化正，大化小，化到锐角为终了．
②化简：统一角，统一名，同角名少为终了．
2.常见的互余关系有与，与，与等；
探究一：诱导公式一的应用
在平面直角坐标系中，角与角均以为始边，它们的终边关于轴对称，若，则（ ）
A．B．C．D．
思路分析：
根据终边关于y轴对称可得关系，再利用诱导公式，即可得答案；
【变式练习】
1．函数，的图象与直线的交点的个数为（ ）
A．0B．1C．2D．3
2．设，则的大小关系是（ ）
A．B．
C．D．
探究二：诱导公式二、三、四的应用
若，，则（ ）
A．B．C．D．
思路分析：
根据诱导公式及三角函数的值在各象限的符号，再利用同角三角函数的平方关系即可求解.
【变式练习】
1．若为任意角，则满足的一个的值为（ ）
A．1B．2C．3D．4
2．如图，一质点在半径为1的圆O上以点为起点，按顺时针方向做匀速圆周运动，角速度为，5s时到达点，则（ ）
A．-1B．C．D．
探究三：诱导公式五、六的应用
已知角 的终边经过点 ，则 的值为（ ）
A．B．C．D．
思路分析：
根据三角函数的定义，求得，再结合诱导公式，得到，即可求解.
【变式练习】
1．设α为锐角，若cs＝－，则sin的值为（ ）
A．－ B．C．－D．
2．已知锐角终边上一点A的坐标为，则角的弧度数为（ ）
A．B．C．D．
探究四：利用诱导公式证明三角恒等式
若角的终边落在直线上，则_____．
思路分析：
化简得到，考虑角为第一或第三象限角两种情况，计算得到答案.
【变式练习】
1．若cs α＝，且α是第四象限角，则cs(α＋)＝________．
2．若是锐角三角形的内角，则点在第_____________象限.
探究五：利用诱导公式进行三角函数的化简求值
化简：＝________.
思路分析：
由诱导公式可得，整体代入原式结合三角函数公式化简可得出答案.
【变式练习】
1．若，，则___________.
2．______．
一、单选题
1．（ ）
A．B．C．D．
2．（ ）
A．B．C．D．1
3．按从小到大排列的顺序为（ ）
A．B．
C．D．
4．（ ）
A．B．C．D．
5．若，则函数的最大值与最小值之和为（ ）
A．B．C．D．
6．已知为第三象限角，，则等于（ ）
A．B．C．D．
7．（ ）
A．3B．4C．D．
8．已知角的终边与单位圆相交于点，，则（ ）
A．B．C．D．
二、多选题
9．下列各式化简中，正确的是（ ）
A．B．
C．D．
10．下列函数中是奇函数的是（ ）
A．B．y=x-3
C．D．
11．已知，，则可能等于（ ）
A．B．C．D．
12．在平面直角坐标系中，O是坐标原点，点（cs，sin），，则下列说法正确的是（ ）
A．线段与的长均为1B．线段的长为1
C．若点，关于y轴对称，则D．当时，点，关于x轴对称
三、填空题
13．在平面直角坐标系中，动点在单位圆上按逆时针方向作匀速圆周运动，每12分钟转动一周.若点的初始位置坐标为，则运动到3分钟时，动点所处位置的坐标是____________.
14．已知，则___________.
15．已知角的终边经过点，将角的终边绕原点顺时针旋转得到角的终边，则___________.
16．计算__________．
四、解答题
17．（1）已知，求的值.
（2）求的值.
18．
(1)化简：；
(2)已知角的终边经过点，求，的值；
19．已知．
(1)求的值；
(2)若为第四象限角，求的值．
20．已知，
(1)求，；
(2)求.
21．已知，为第二象限角.
(1)若，求的值；
(2)若，求的值.
22．(1)请化简：．
(2)已知,,求.
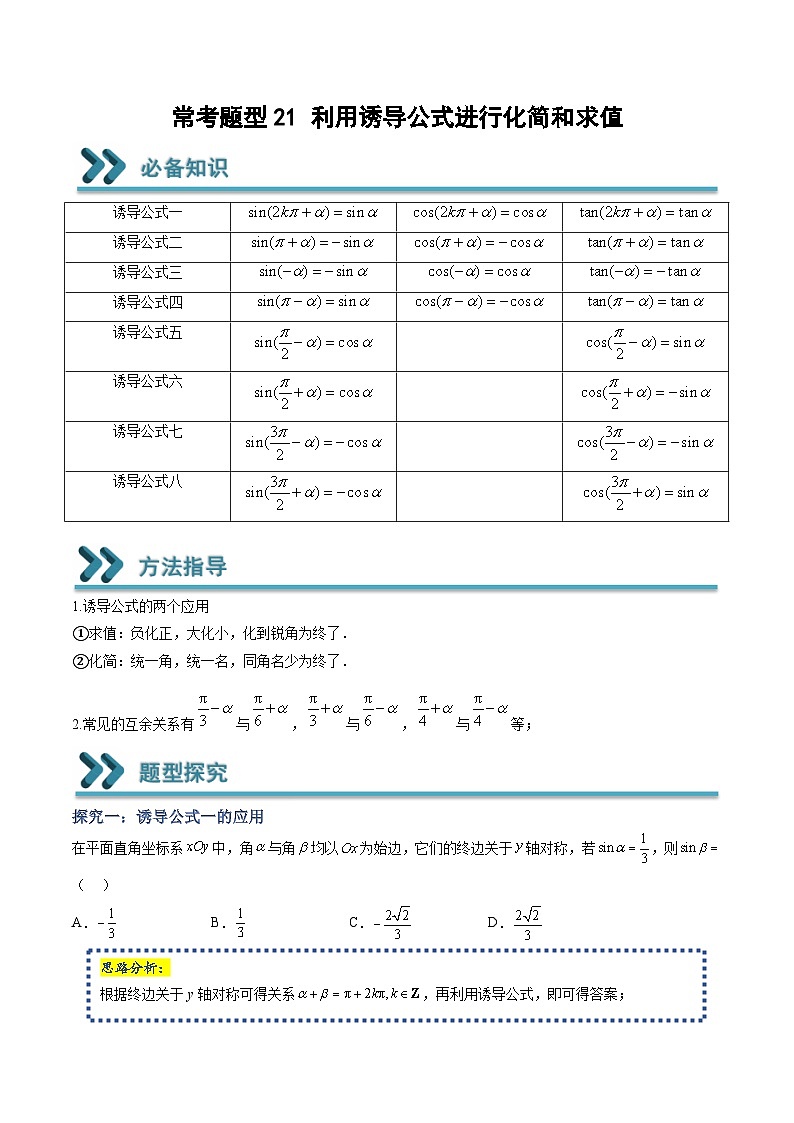
诱导公式一
诱导公式二
诱导公式三
诱导公式四
诱导公式五
诱导公式六
诱导公式七
诱导公式八
常考题型21 利用诱导公式进行化简和求值
1.诱导公式的两个应用
①求值：负化正，大化小，化到锐角为终了．
②化简：统一角，统一名，同角名少为终了．
2.常见的互余关系有与，与，与等；
探究一：诱导公式一的应用
在平面直角坐标系中，角与角均以为始边，它们的终边关于轴对称，若，则（ ）
A．B．C．D．
思路分析：
根据终边关于y轴对称可得关系，再利用诱导公式，即可得答案；
答案：B
【详解】在平面直角坐标系xOy中，角与角均以Ox为始边，它们的终边关于y轴对称，
∴，
∵，
∴
故选：B.
【变式练习】
1．函数，的图象与直线的交点的个数为（ ）
A．0B．1C．2D．3
答案：C
【详解】的图象与直线的交点的个数，
即方程在区间上的解的个数，
由在区间上的解为或，
可得方程在区间上的解的个数为2，故选C.
2．设，则的大小关系是（ ）
A．B．
C．D．
答案：B
【详解】解：因为，
，
则，
因为，
即，
所以，
故选：B
探究二：诱导公式二、三、四的应用
若，，则（ ）
A．B．C．D．
思路分析：
根据诱导公式及三角函数的值在各象限的符号，再利用同角三角函数的平方关系即可求解.
答案：A
【详解】由，得，又，所以，
所以.
故选：A.
【变式练习】
1．若为任意角，则满足的一个的值为（ ）
A．1B．2C．3D．4
答案：B
【详解】因为，所以，即，
所以满足条件的一个的值为2.故选：B
2．如图，一质点在半径为1的圆O上以点为起点，按顺时针方向做匀速圆周运动，角速度为，5s时到达点，则（ ）
A．-1B．C．D．
答案：C
【详解】设单位圆与轴正半轴的交点为，则，所以，，故.
故选：C
探究三：诱导公式五、六的应用
已知角 的终边经过点 ，则 的值为（ ）
A．B．C．D．
思路分析：
根据三角函数的定义，求得，再结合诱导公式，得到，即可求解.
答案：A
【详解】由题意，角的终边经过点，可得，
根据三角函数的定义，可得，
又由.
故选：A.
【变式练习】
1．设α为锐角，若cs＝－，则sin的值为（ ）
A．－ B．C．－D．
答案：D
【详解】因为，所以，
所以.
故选：D.
2．已知锐角终边上一点A的坐标为，则角的弧度数为（ ）
A．B．C．D．
答案：A
【详解】，
又，为锐角，
∴ ，
故选：A.
探究四：利用诱导公式证明三角恒等式
若角的终边落在直线上，则_____．
思路分析：
化简得到，考虑角为第一或第三象限角两种情况，计算得到答案.
答案：或
【详解】因为角的终边落在直线上，所以角为第一或第三象限角，
，
当角为第一象限角时，，；
当角为第三象限角时，，．
故答案为：或.
【变式练习】
1．若cs α＝，且α是第四象限角，则cs(α＋)＝________．
答案：
【详解】由题意得sin α＝－＝－，所以cs(α＋)＝－sin α＝．
故答案为：
2．若是锐角三角形的内角，则点在第_____________象限.
答案：二
【详解】由题得,因为锐角三角形,
故,故,即.
又,同理.即.
故点在第二象限.
故答案为：二
探究五：利用诱导公式进行三角函数的化简求值
化简：＝________.
思路分析：
由诱导公式可得，整体代入原式结合三角函数公式化简可得出答案.
答案：
【详解】原式=
故答案为：
【变式练习】
1．若，，则___________.
答案：-1
【详解】因为，所以，
所以，
所以，即或,
当时，
因为，所以，
所以，所以，所以，
所以.
当时，即，
所以，
所以，则.
因为，所以，所以，
故不符合题意，应舍去，
综合以上，
故答案为：-1
2．______．
答案：
【详解】由题意，原式=
.
故答案为：.
一、单选题
1．（ ）
A．B．C．D．
答案：D
【详解】.故选：D.
2．（ ）
A．B．C．D．1
答案：B
【详解】.故选：B
3．按从小到大排列的顺序为（ ）
A．B．
C．D．
答案：B
【详解】，
因为，在上为增函数，
所以，
所以，
故选：B
4．（ ）
A．B．C．D．
答案：B
【详解】；故选：B．
5．若，则函数的最大值与最小值之和为（ ）
A．B．C．D．
答案：C
【详解】，
当时，，，
当时，；当时，；
.
故选：C.
6．已知为第三象限角，，则等于（ ）
A．B．C．D．
答案：D
【详解】由，则，又为第三象限角，
所以，则，，
目标式可化为.
故选：D
7．（ ）
A．3B．4C．D．
答案：B
【详解】
＝．
故选：B．
8．已知角的终边与单位圆相交于点，，则（ ）
A．B．C．D．
答案：D
【详解】角的终边与单位圆相交于点P(sin11π6,cs11π6),
.
故选：D.
二、多选题
9．下列各式化简中，正确的是（ ）
A．B．
C．D．
答案：ACD
【详解】A：，正确；
B：，错误；
C：，正确；
D：，故，
而，
所以，正确.
故选：ACD
10．下列函数中是奇函数的是（ ）
A．B．y=x-3
C．D．
答案：BCD
【详解】根据题意，依次分析选项：
对于A，，其定义域为[0，+∞），不是奇函数，不符合题意；
对于B，设，其定义域为，有，是奇函数，符合题意；
对于C，，是奇函数，符合题意；
对于D，设，有，解可得，即函数的定义域为，且，函数是奇函数，符合题意.
故选：BCD
11．已知，，则可能等于（ ）
A．B．C．D．
答案：BD
【详解】解：因为，
所以由得，
所以，
因为
所以可能等于或
故选：BD
12．在平面直角坐标系中，O是坐标原点，点（cs，sin），，则下列说法正确的是（ ）
A．线段与的长均为1B．线段的长为1
C．若点，关于y轴对称，则D．当时，点，关于x轴对称
答案：ACD
【详解】，同理可求，A正确；
由题意得：，由勾股定理得：，B错误；
若点，关于y轴对称，则，，则，，解得：，C正确；
当时，，即，即，关于x轴对称，D正确.
故选：ACD
三、填空题
13．在平面直角坐标系中，动点在单位圆上按逆时针方向作匀速圆周运动，每12分钟转动一周.若点的初始位置坐标为，则运动到3分钟时，动点所处位置的坐标是____________.
答案：
【详解】解：由题意可得图：
每12分钟转动一周，则运动到3分钟时，转过的角为；
点的初始位置坐标为，若角的始边为轴的非负半轴，此时角终边所在直线为，则
运动到3分钟时，形成的角度为，
所以
动点所处位置的坐标是．
故答案为：．
14．已知，则___________.
答案：
【详解】因为，
所以.
故答案为：.
15．已知角的终边经过点，将角的终边绕原点顺时针旋转得到角的终边，则___________.
答案：
【详解】因为角的终边经过点，
所以，则，
又因为角的终边绕原点顺时针旋转得到角的终边，故，
所以，
故.
故答案为：.
16．计算__________．
答案：
【详解】
.
故答案为：
四、解答题
17．（1）已知，求的值.
（2）求的值.
答案：（1）2；（2）
【详解】解：（1）因为，
所以；
（2）.
18．
(1)化简：；
(2)已知角的终边经过点，求，的值；
答案：(1)
(2)，.
【详解】（1）.
（2）因为角的终边经过点，所以，
所以，.
19．已知．
(1)求的值；
(2)若为第四象限角，求的值．
答案：(1)；(2)
【详解】（1）由题意得，
.
（2）由，得，
代入，得，
因为为第四象限角，所以，
，
故．
20．已知，
(1)求，；
(2)求.
答案：(1)答案见解析；(2)
【详解】（1）由为第一或第三象限角
又，则，联立
解得，
①当为第一象限角时
则，
②当为第三象限角时
则，
（2）原式
21．已知，为第二象限角.
(1)若，求的值；
(2)若，求的值.
答案：(1)；(2)
【详解】（1）为第二象限角，则.
.
∵，∴.
∴.
（2），
则.
∵为第二象限角，
∴，，.
∴
.
22．(1)请化简：．
(2)已知,,求.
答案：（1）；（2）
【详解】（1）原式=
（2）因为，两边平方得，
有
所以
又因为，所以，，则
所以．
诱导公式一
诱导公式二
诱导公式三
诱导公式四
诱导公式五
诱导公式六
诱导公式七
诱导公式八