

人教A版高一数学上学期期中期末必考题型归纳及过关测试专题14对数函数及其性质(原卷版+解析)
展开知识点一、对数函数的概念
1、函数叫做对数函数.其中是自变量,函数的定义域是,值域为.
2、判断一个函数是对数函数是形如的形式,即必须满足以下条件:
(1)系数为1;
(2)底数为大于0且不等于1的常数;
(3)对数的真数仅有自变量.
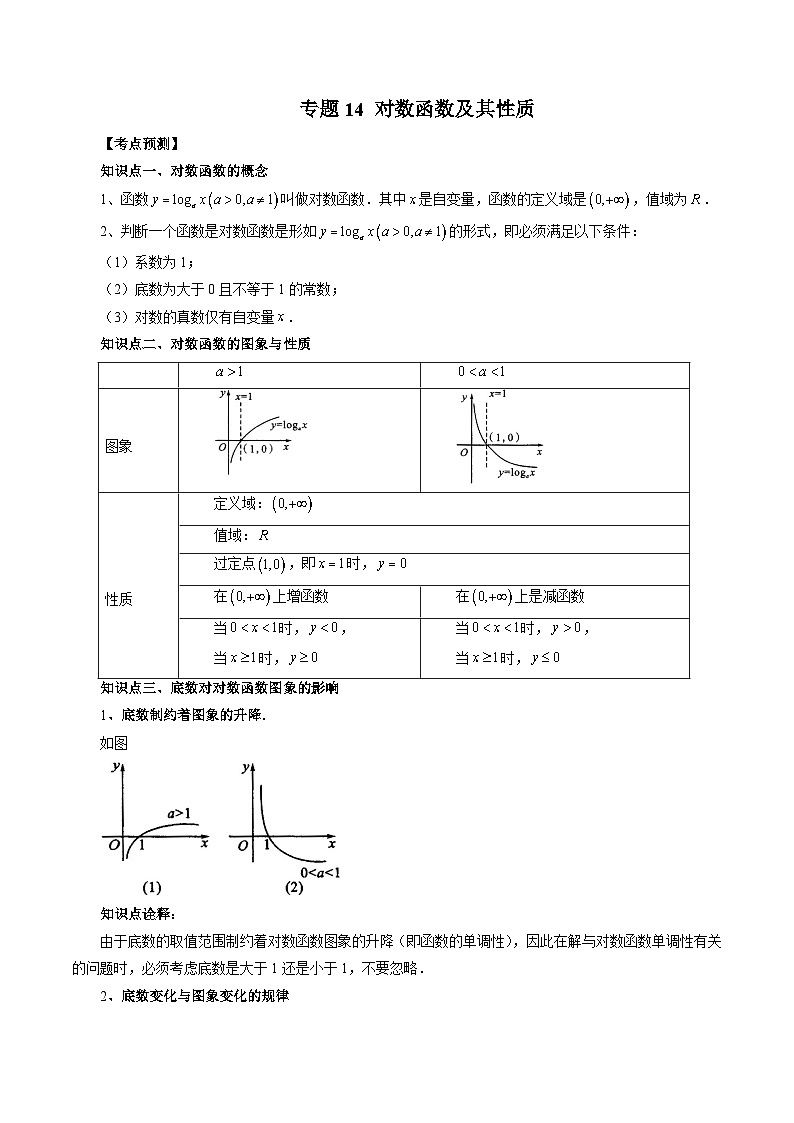
知识点二、对数函数的图象与性质
知识点三、底数对对数函数图象的影响
1、底数制约着图象的升降.
如图
知识点诠释:
由于底数的取值范围制约着对数函数图象的升降(即函数的单调性),因此在解与对数函数单调性有关的问题时,必须考虑底数是大于1还是小于1,不要忽略.
2、底数变化与图象变化的规律
在同一坐标系内,当时,随a的增大,对数函数的图像愈靠近x轴;当时,对数函数的图象随a的增大而远离x轴.(见下图)
知识点四、反函数
1、反函数的定义
设分别为函数的定义域和值域,如果由函数所解得的也是一个函数(即对任意的一个,都有唯一的与之对应),那么就称函数是函数的反函数,记作,在中,是自变量,是的函数,习惯上改写成()的形式.函数()与函数()为同一函数,因为自变量的取值范围即定义域都是B,对应法则都为.
由定义可以看出,函数的定义域A正好是它的反函数的值域;函数的值域B正好是它的反函数的定义域.
2、反函数的性质
(1)互为反函数的两个函数的图象关于直线对称.
(2)若函数图象上有一点,则必在其反函数图象上,反之,若在反函数图象上,则必在原函数图象上.
【典型例题】
例1.(2023·北京·北二外附属中学高一期中)已知.
(1)求函数的定义域;
(2)判断函数的奇偶性,并加以证明;
(3)求的值;
(4)证明函数在上为单调递减函数.
例2.(2023·上海市嘉定区第一中学高一阶段练习)已知函数的定义域是关于的不等式的解集
(1)求以上不等式的解集;
(2)求函数的最大值和最小值,并求出此时的值.
例3.(2023·河南·郑州外国语学校高一期中)(1)若函数的定义域为,求的范围;
(2)若函数的值域为,求的范围.
例4.(2023·宁夏·银川二中高一期中)已知函数,其中,均为实数.
(1)若,且的定义域为,求的取值范围;
(2)若,是否存在实数,使得在区间内单调递增?若存在,求出的取值范围;若不存在,请说明理由.
【过关测试】
一、单选题
1.(2023·黑龙江·哈师大附中高一期中)函数的增区间为( )
A.B.C.D.
2.(2023·四川·树德中学高一阶段练习)已知函数的图象如图所示,则( )
A.B.C.D.
3.(2023·湖南·邵阳市第二中学高一期中)已知定义域为的奇函数满足,,则不等式的解集为( )
A.B.
C.D.
4.(2023·吉林·长春市第二实验中学高一期中)已知的值域为R,那么实数a的取值范围是( )
A.B.
C.D.
5.(2023·广东·广州市第一中学高一期中)已知函数,若对任意的,存在,使得,则实数的取值范围是( )
A.B.C.D.
6.(2023·上海·高一专题练习)函数的反函数为,则的根有( )个
A.B.C.D.
7.(2023·广东·深圳市龙岗区龙城高级中学高一期中)设满足,满足,则( )
A.B.C.D.
8.(2023·江苏省上冈高级中学高一期中)若在区间上是减函数,则实数a的取值范围为( )
A.B.
C.D.
二、多选题
9.(2023·安徽·淮北一中高一期中)已知函数,则下列说法正确的是( )
A. 的定义域为B.为奇函数
C.在定义域上是增函数D.的值域为
10.(2023·福建·三明一中高一期中)下列说法中正确的是( )
A.若函数是奇函数,则
B.函数的值域为,则实数的取值范围是
C.函数与的图象关于对称
D.函数与函数为同一函数
11.(2023·四川·树德中学高一阶段练习)已知函数,函数满足.则( )
A.
B.函数的图象关于点对称
C.若实数a、b满足,则
D.若函数与图象的交点为,则
12.(2023·浙江大学附属中学高一期末)已知函数,,且,下列结论正确的是( )
A.B.
C.D.
三、填空题
13.(2023·江苏省上冈高级中学高一期中)已知函数,则函数的定义域为_________
14.(2023·河南·郑州外国语学校高一期中)已知函数在上单调递增,则实数的取值范围为______.
15.(2023·四川·树德中学高一阶段练习)己知函数是偶函数,在区间内单调递减,,则不等式的解集为__________.
16.(2023·河南·郑州外国语学校高一期中)已知,,若,,使得,则实数的最大值是______.
四、解答题
17.(2023·山西·运城市景胜中学高一阶段练习)已知.
(1)求的定义域;
(2)判断的奇偶性并加以说明;
(3)求使的的取值范围.
18.(2023·福建·三明一中高一期中)已知函数
(1)求不等式的解集;
(2)若对于任意恒成立,求的取值范围.
19.(2023·河南·郑州外国语学校高一期中)设函数.
(1)解方程;
(2)设不等式的解集为,求函数的值域.
20.(2023·全国·高一课时练习)已知函数.
(1)若的值域为R,求实数m的取值范围;
(2)若在内单调递增,求实数m的取值范围.
21.(2023·福建省漳州第一中学高一开学考试)已知函数是的反函数,当时,函数,()的最小值为.
(1)求的函数表达式;
(2)是否存在实数,使得函数的定义域为,值域为,若存在求出、的值,若不存在,请说明理由.
22.(2023·上海·高一专题练习)已知函数,.
(1)如果,求函数的值域;
(2)求函数的最大值;
(3)如果对任意,不等式恒成立,求实数的取值范围.
图象
性质
定义域:
值域:
过定点,即时,
在上增函数
在上是减函数
当时,,
当时,
当时,,
当时,
专题14 对数函数及其性质
【考点预测】
知识点一、对数函数的概念
1、函数叫做对数函数.其中是自变量,函数的定义域是,值域为.
2、判断一个函数是对数函数是形如的形式,即必须满足以下条件:
(1)系数为1;
(2)底数为大于0且不等于1的常数;
(3)对数的真数仅有自变量.
知识点二、对数函数的图象与性质
知识点三、底数对对数函数图象的影响
1、底数制约着图象的升降.
如图
知识点诠释:
由于底数的取值范围制约着对数函数图象的升降(即函数的单调性),因此在解与对数函数单调性有关的问题时,必须考虑底数是大于1还是小于1,不要忽略.
2、底数变化与图象变化的规律
在同一坐标系内,当时,随a的增大,对数函数的图像愈靠近x轴;当时,对数函数的图象随a的增大而远离x轴.(见下图)
知识点四、反函数
1、反函数的定义
设分别为函数的定义域和值域,如果由函数所解得的也是一个函数(即对任意的一个,都有唯一的与之对应),那么就称函数是函数的反函数,记作,在中,是自变量,是的函数,习惯上改写成()的形式.函数()与函数()为同一函数,因为自变量的取值范围即定义域都是B,对应法则都为.
由定义可以看出,函数的定义域A正好是它的反函数的值域;函数的值域B正好是它的反函数的定义域.
2、反函数的性质
(1)互为反函数的两个函数的图象关于直线对称.
(2)若函数图象上有一点,则必在其反函数图象上,反之,若在反函数图象上,则必在原函数图象上.
【典型例题】
例1.(2023·北京·北二外附属中学高一期中)已知.
(1)求函数的定义域;
(2)判断函数的奇偶性,并加以证明;
(3)求的值;
(4)证明函数在上为单调递减函数.
【解析】(1)由题意,解得,
定义域为;
(2)是偶函数:
证明:,所以是偶函数;
(3);
(4)设,
,
∵,所以,,,
∴,即,
∴函数在上为单调递减函数.
例2.(2023·上海市嘉定区第一中学高一阶段练习)已知函数的定义域是关于的不等式的解集
(1)求以上不等式的解集;
(2)求函数的最大值和最小值,并求出此时的值.
【解析】(1)由可得,
即,则,即,
所以 ,即的解集为.
(2)因为,
令 ,则 ,
当即时,,即取得最小值;
当或即或时,,即取得最大值;
例3.(2023·河南·郑州外国语学校高一期中)(1)若函数的定义域为,求的范围;
(2)若函数的值域为,求的范围.
【解析】(1)的定义域为,对恒成立;
当时,不等式变为,即,不合题意;
当时,若恒成立,则,解得:;
综上所述:实数的取值范围为;
(2)设的值域为,
的值域为,;
当时,,则,满足题意;
当时,若,则,解得:;
综上所述:实数的取值范围为.
例4.(2023·宁夏·银川二中高一期中)已知函数,其中,均为实数.
(1)若,且的定义域为,求的取值范围;
(2)若,是否存在实数,使得在区间内单调递增?若存在,求出的取值范围;若不存在,请说明理由.
【解析】(1)当时,的定义域为,
则,解得:;
(2)当时,,
函数拆分成内外层函数,,,若函数在区间内单调递增,则内层函数在上单调递减,并且,
当时,在上单调递减,并且,满足条件,
当时,需满足下列条件
则,解得:,
综上可知存在实数,的取值范围是.
【过关测试】
一、单选题
1.(2023·黑龙江·哈师大附中高一期中)函数的增区间为( )
A.B.C.D.
答案:D
【解析】由得,
解得,
的开口向下,对称轴为,
函数在上递减,
根据复合函数单调性同增异减可知,的增区间为.
故选:D
2.(2023·四川·树德中学高一阶段练习)已知函数的图象如图所示,则( )
A.B.C.D.
答案:C
【解析】由图象知最上方的图象是的图象,过点的是的图象,过点的是的图象,
因此,,,
,,,即,
故选:C.
3.(2023·湖南·邵阳市第二中学高一期中)已知定义域为的奇函数满足,,则不等式的解集为( )
A.B.
C.D.
答案:B
【解析】因为,
所以,时,;当时,;
因为函数是定义域为的奇函数,
所以,时,;时,;时,.
所以,的解集为.
故选:B
4.(2023·吉林·长春市第二实验中学高一期中)已知的值域为R,那么实数a的取值范围是( )
A.B.
C.D.
答案:A
【解析】当时,函数在上单调递增,其取值集合为,而函数的值域为R,
因此函数在上的取值集合包含,
当时,函数在上的值为常数,不符合要求,
当时,函数在上单调递减,取值集合是,不符合要求,
于是得,函数在上单调递增,取值集合是,则,解得,
所以实数a的取值范围是.
故选:A
5.(2023·广东·广州市第一中学高一期中)已知函数,若对任意的,存在,使得,则实数的取值范围是( )
A.B.C.D.
答案:A
【解析】对任意的,存在,使得,则,
因为当时,单调递增,所以,
又因为当时,单调递减,所以,
所以由解得,
故选:A.
6.(2023·上海·高一专题练习)函数的反函数为,则的根有( )个
A.B.C.D.
答案:D
【解析】因为,则.
①当时,,令,解得;
②当时,,令,解得.
因此,方程的根有个.
故选:D.
7.(2023·广东·深圳市龙岗区龙城高级中学高一期中)设满足,满足,则( )
A.B.C.D.
答案:D
【解析】根据题意,
令,则,
即,
因为函数在上单调递增,
又满足,
所以,
所以,
即,
所以.
故选:D.
8.(2023·江苏省上冈高级中学高一期中)若在区间上是减函数,则实数a的取值范围为( )
A.B.
C.D.
答案:A
【解析】设,
由题意得:在上恒成立,
且由复合函数单调性“同增异减”原则可知:
函数在上单调递减,
则有,解得:.
故选:A
二、多选题
9.(2023·安徽·淮北一中高一期中)已知函数,则下列说法正确的是( )
A. 的定义域为B.为奇函数
C.在定义域上是增函数D.的值域为
答案:ABC
【解析】的定义域为,
又,
所以为奇函数,故AB正确;
,因为 在为增函数,
由复合函数的单调性可知在定义域上单调递增,故C正确.
因为函数定义域为.
时,
故
的值域为,故D错误.
故选:ABC.
10.(2023·福建·三明一中高一期中)下列说法中正确的是( )
A.若函数是奇函数,则
B.函数的值域为,则实数的取值范围是
C.函数与的图象关于对称
D.函数与函数为同一函数
答案:BC
【解析】是奇函数,且在原点有定义,则,比如是奇函数,则无意义,故A错误,
的值域为,则能够取遍所有的正数,当满足题意,当 ,则 且 ,故 ,因此 ,故B正确,
函数与互为反函数,故其图象关于对称,C正确,
由于函数,,两函数的对应关系不一样,故不是同一函数,D错误,
故选:BC
11.(2023·四川·树德中学高一阶段练习)已知函数,函数满足.则( )
A.
B.函数的图象关于点对称
C.若实数a、b满足,则
D.若函数与图象的交点为,则
答案:ABC
【解析】对于A选项,由函数,函数定义域为R,则
所以
,所以,故A选项正确.
对于B选项,因为满足,的图象关于点成中心对称.故B选项正确.
对于C选项,设,则,则为奇函数,由函数单调性的性质可知,当时,单调递增,所以在R上为增函数,则也为R上的增函数,因为实数a、b满足,且,则,即,所以,即.故C选项正确.
对于D选项,由,,的图象关于点成中心对称,的图象也关于点成中心对称,令,则,因为函数与图象的交点为,不妨设,由对称性可知,,所以,则.故D选项错误.
故选:ABC
12.(2023·浙江大学附属中学高一期末)已知函数,,且,下列结论正确的是( )
A.B.
C.D.
答案:CD
【解析】由题意得,且,则,
故,故A错误,
对于B,,而,故,故B错误,
对于C,,故C正确,
对于D,,故D正确,
故选:CD
三、填空题
13.(2023·江苏省上冈高级中学高一期中)已知函数,则函数的定义域为_________
答案:
【解析】因为,所以,解得,即的定义域为,
对于,则,解得,
所以的定义域为.
故答案为:
14.(2023·河南·郑州外国语学校高一期中)已知函数在上单调递增,则实数的取值范围为______.
答案:
【解析】在上单调递增,,解得:,
即实数的取值范围为.
故答案为:.
15.(2023·四川·树德中学高一阶段练习)己知函数是偶函数,在区间内单调递减,,则不等式的解集为__________.
答案:
【解析】因为函数是偶函数,关于轴对称,向左平移1个单位后得函数,函数关于直线对称,因为函数在区间内单调递减,,所以函数在区间单调递增,且,
不等式等价于,即,解得:或;
或,即 ,解集为;
综上可知,不等式的解集为.
故答案为:
16.(2023·河南·郑州外国语学校高一期中)已知,,若,,使得,则实数的最大值是______.
答案:
【解析】,,使得,;
在上单调递减,;
在上单调递增,在上单调递增,
在上单调递增,;
,解得:,则实数的最大值为.
故答案为:.
四、解答题
17.(2023·山西·运城市景胜中学高一阶段练习)已知.
(1)求的定义域;
(2)判断的奇偶性并加以说明;
(3)求使的的取值范围.
【解析】(1)由题意得函数要有意义则:
故的定义域为.
(2)为奇函数,理由如下:
由(1)知的定义域关于原点对称,
由,
所以
故函数是奇函数.
(3)由>0可得,
所以,
即
解得,
故求使>0的的取值范围是(0,1).
18.(2023·福建·三明一中高一期中)已知函数
(1)求不等式的解集;
(2)若对于任意恒成立,求的取值范围.
【解析】(1)
由,即
计算可得或
或
故解集为:或;
(2)令,则,原式可化为在上恒成立,
记函数在上单调递增,
,故的取值范围是.
19.(2023·河南·郑州外国语学校高一期中)设函数.
(1)解方程;
(2)设不等式的解集为,求函数的值域.
【解析】(1)
,
由得,解得或,
所以或.
所以方程的解是或;
(2)由得,即,解得,,
,
令,所以,
则为开口向上对称轴为的抛物线,
因为,所以,
所以函数的值域为.
20.(2023·全国·高一课时练习)已知函数.
(1)若的值域为R,求实数m的取值范围;
(2)若在内单调递增,求实数m的取值范围.
【解析】(1)由的值域为R,可得能取内的一切值,
故函数的图象与x轴有公共点,
所以,解得或.
故实数m的取值范围为.
(2)因为在内单调递增,
所以在内单调递减且恒正,
所以,解得.
故实数m的取值范围为.
21.(2023·福建省漳州第一中学高一开学考试)已知函数是的反函数,当时,函数,()的最小值为.
(1)求的函数表达式;
(2)是否存在实数,使得函数的定义域为,值域为,若存在求出、的值,若不存在,请说明理由.
【解析】(1)因为函数是的反函数,
所以,
则,
令,则,,
所以,对称轴为,
①当时,的最小值为;
②当时,在,上单调递增,所以的最小值;
③当时,在,上单调递减,所以的最小值为.
综上所述,;
(2)当时, ,
故当时,为单调递减函数,
所以在,上的值域为,,
则,
两式相减可得,,
因为,所以,
将代入方程中求解,无实数根,
故不存在实数,使得函数的定义域为,,值域为,.
22.(2023·上海·高一专题练习)已知函数,.
(1)如果,求函数的值域;
(2)求函数的最大值;
(3)如果对任意,不等式恒成立,求实数的取值范围.
【解析】(1),令,,,
则.
当时,取得最大值为,当时,函数取得最小值为,
的值域为.
(2)函数,
,
当时,,.
当时,,.
即
当时,最大值为1;当时,.
综上:当时,取到最大值为1.
(3)对任意,不等式恒成立,
即.
,,对一切恒成立.
当时,.
当,,在上是减函数,,.
综上所述,的取值范围为.
图象
性质
定义域:
值域:
过定点,即时,
在上增函数
在上是减函数
当时,,
当时,
当时,,
当时,
人教A版高一数学上学期期中期末必考题型归纳及过关测试专题07函数的概念、定义域、值域、解析式、分段函数(原卷版+解析): 这是一份人教A版高一数学上学期期中期末必考题型归纳及过关测试专题07函数的概念、定义域、值域、解析式、分段函数(原卷版+解析),共30页。试卷主要包含了函数的概念,区间,函数的三要素,函数的相等,函数的表示方法,分段函数等内容,欢迎下载使用。
人教A版高一数学上学期期中期末必考题型归纳及过关测试专题06含参数二次函数的最值、单调性、恒成立问题(原卷版+解析): 这是一份人教A版高一数学上学期期中期末必考题型归纳及过关测试专题06含参数二次函数的最值、单调性、恒成立问题(原卷版+解析),共23页。试卷主要包含了一元二次不等式等内容,欢迎下载使用。
人教A版高一数学上学期期中期末必考题型归纳及过关测试专题05利用基本不等式求最值(原卷版+解析): 这是一份人教A版高一数学上学期期中期末必考题型归纳及过关测试专题05利用基本不等式求最值(原卷版+解析),共21页。试卷主要包含了重要不等式,基本不等式,与基本不等式相关的不等式,利用基本不等式求最值等内容,欢迎下载使用。












