2024年高考数学一轮复习满分攻略(新高考地区专用)考点02逻辑用语与充分、必要条件(精讲)(原卷版+解析)

这是一份2024年高考数学一轮复习满分攻略(新高考地区专用)考点02逻辑用语与充分、必要条件(精讲)(原卷版+解析)，共43页。试卷主要包含了充分条件，全称命题和特称命题等内容，欢迎下载使用。

1、充分条件、必要条件与充要条件的概念
①定义法判断充分条件、必要条件
牢记：小范围可以推大范围，大范围不可以推小范围
注：注意区别是的充分不必要条件与的充分不必要条件是两者的不同．
（1）是的充分不必要条件且（注意标志性词：“是”，此时与正常顺序）
（2）的充分不必要条件是且（注意标志性词：“的”，此时与倒装顺序）
②集合判断法判断充分条件、必要条件
若以集合的形式出现，以集合的形式出现，即：，：，则
（1）若，则是的充分条件；
（2）若，则是的必要条件；
（3）若，则是的充分不必要条件；
（4）若，则是的必要不充分条件；
（5）若，则是的充要条件；
（6）若且，则是的既不充分也不必要条件.
③传递法判断充分条件、必要条件
（1） 若 是 的充分条件， 是 的充分条件，则 是 的充分条件;
（2） 若 是 的必要条件， 是 的必要条件，则 是 的必要条件;
（3） 若 是 的充要条件，是 的充要条件，则 是 的充要条件．
④等价转化法判断充分条件、必要条件
由于互为逆否命题的两个命题具有相同的真假性，因而，当判断原命题真假比较困难时（特别是那些带有否定性的命题），可转化为判断它的逆否命题的真假，这就是常说的"正难则反".
（1）是的充分不必要条件是的充分不必要条件；
（2）是的必要不充分条件是的必要不充分条件；
（3）是的充要条件是的充要条件；
（4）是的既不充分也不必要条件是的既不充分也不必要条件.
2、全称命题和特称命题
（1）全称量词和存在量词
（2）全称命题和存在命题
（3）全称命题与特称命题的否定
①对含有一个量词的全称命题的否定
全称命题：，
的否定：，；
从一般形式来看，全称命题“对M中任意一个x，有p（x）成立”，它的否定并不是简单地对结论部分p(x)进行否定，还需对全称量词进行否定，使之成为存在量词，也即“任意”的否定为“，”.
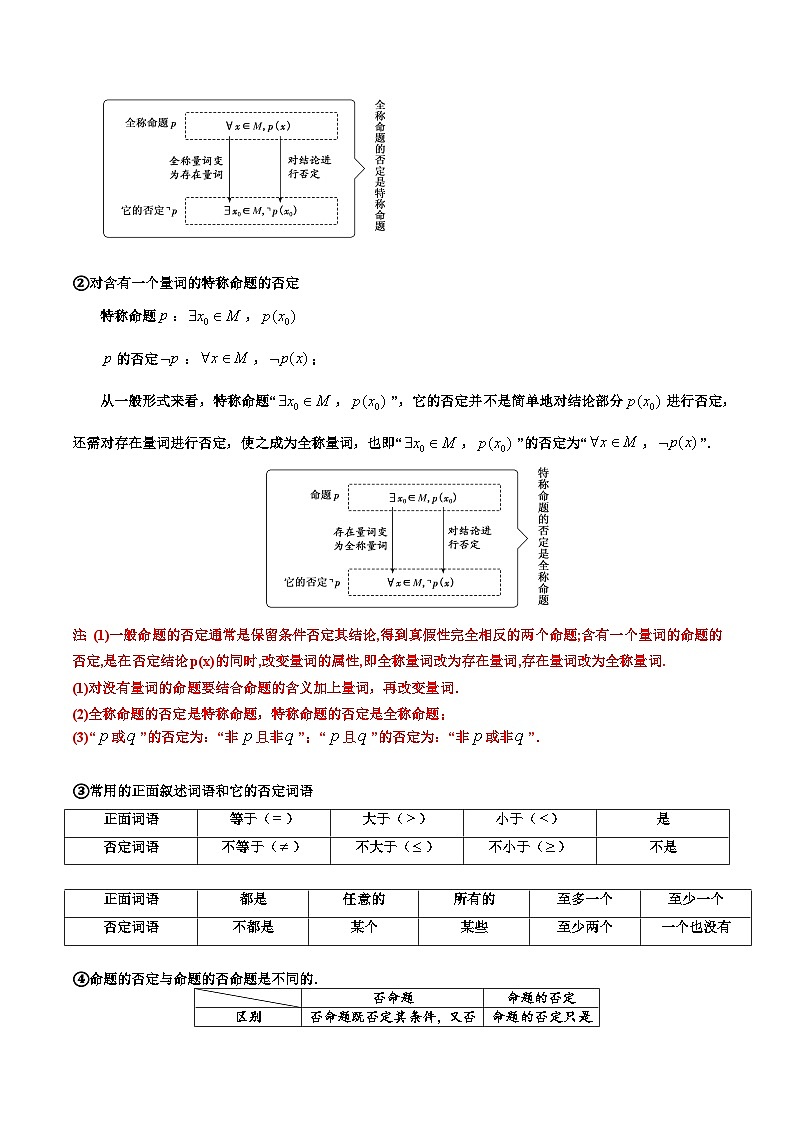
②对含有一个量词的特称命题的否定
特称命题：，
的否定：，；
从一般形式来看，特称命题“，”，它的否定并不是简单地对结论部分进行否定，还需对存在量词进行否定，使之成为全称量词，也即“，”的否定为“，”.
存在命题
注：(1)一般命题的否定通常是保留条件否定其结论,得到真假性完全相反的两个命题;含有一个量词的命题的否定,是在否定结论p(x)的同时,改变量词的属性,即全称量词改为存在量词,存在量词改为全称量词.
(1)对没有量词的命题要结合命题的含义加上量词，再改变量词．
(2)全称命题的否定是特称命题，特称命题的否定是全称命题；
(3)“或”的否定为：“非且非”；“且”的否定为：“非或非”．
③常用的正面叙述词语和它的否定词语
④命题的否定与命题的否命题是不同的.
拓展：
1、四种命题
(1)四种命题及其相互关系
(2)互为逆否命题的真假判断：
互为逆否的两个命题同真或同假．
注：①任何命题都可写为：“若p则q”形式．②一个命题要么是真命题，要么是假命题，不能模棱两可．
2、命题p∧q，p∨q，¬p的真假判断
注：①明晰一种关系
逻辑联结词与集合的关系：“或、且、非”三个逻辑联结词，对应着集合运算中的“并、交、补”，因此，常常借助集合的“并、交、补”的意义来解答由“或、且、非”三个联结词构成的命题问题．
②巧用一个口诀
含有逻辑联结词的命题真假判断口诀：p∨q→见真即真，
p∧q→见假即假，p与¬p→真假相反．
1．（2023·北京）已知 f(x) 是定义在上 [0,1] 的函数，那么“函数 f(x) 在 [0,1] 上单调递增”是“函数 f(x) 在 [0,1] 上的最大值为 f(1) ”的（ ）
A．充分而不必要条件B．必要而不充分条件
C．充分必要条件D．既不充分也不必要条件
2．（2023·浙江）已知非零向量 a,b,c ，则“ a⋅c=b⋅c ”是“ a=b ”的（ ）
A．充分不必要条件B．必要不充分条件
C．充分必要条件D．既不充分又不必要条件
3．（2023·全国甲卷）等比数列｛an｝的公比为q，前n项和为Sn，设甲：q>0，乙:｛Sn｝是递増数列，则（ ）
A．甲是乙的充分条件但不是必要条件
B．甲是乙的必要条件但不是充分条件
C．甲是乙的充要条件
D．甲既不是乙的充分条件也不是乙的必要条件
4．（2023·天津）已知 a∈R ，则“ a>6 ”是“ a2>36 ”的（ ）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不允分也不必要条件
5．（2023·天津）设 a∈R ，则“ a>1 ”是“ a2>a ”的（ ）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
6．（2023·上海）已知 a 、 b∈R ，则“ a2>b2 ”是“ |a|>|b| ”的（ ）
A．充分非必要条件B．必要非充分条件
C．充要条件D．既非充分又非必要条件
7．（2023·浙江）若a>0，b>0，则“a+b≤4“是“ab≤4”的（ ）
A．充分不必要条件B．必要不充分条件
C．充分必要条件D．既不充分也不必要条件
8．（2023·天津）设 x∈R ，则“ x2−5x0，即a1qn>0，则q>0，所以甲是乙的必要条件；
所以甲是乙的必要条件但不是充分条件.
故答案为：B
4．（2023·天津）已知 a∈R ，则“ a>6 ”是“ a2>36 ”的（ ）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不允分也不必要条件
【解析】当a>6时，a2>36，所以充分性成立；
当a2>36时，a6，所以必要性不成立，
故“a>6”是“a2>36”的充分不必要条件.
故答案为：A
5．（2023·天津）设 a∈R ，则“ a>1 ”是“ a2>a ”的（ ）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
【解析】求解二次不等式 a2>a 可得： a>1 或 a1 是 a2>a 的充分不必要条件.
故答案为：A.
6．（2023·上海）已知 a 、 b∈R ，则“ a2>b2 ”是“ |a|>|b| ”的（ ）
A．充分非必要条件B．必要非充分条件
C．充要条件D．既非充分又非必要条件
【解析】 ∵a2>b2 等价， |a|2>|b|2 ，得“ |a|>|b| ”，
“ a2>b2 ”是“ |a|>|b| ”的充要条件，
故答案为： ．
7．（2023·浙江）若a>0，b>0，则“a+b≤4“是“ab≤4”的（ ）
A．充分不必要条件B．必要不充分条件
C．充分必要条件D．既不充分也不必要条件
【解析】作出直线y=4-x和函数 y=4x 的图象，结合图象的关系，可确定“a+b≤4“是“ab≤4”的充分不必要条件.故答案为：A.
8．（2023·天津）设 x∈R ，则“ x2−5x