高考数学大题精做专题01三角函数中的性质问题(原卷版+解析)

这是一份高考数学大题精做专题01三角函数中的性质问题(原卷版+解析)，共25页。
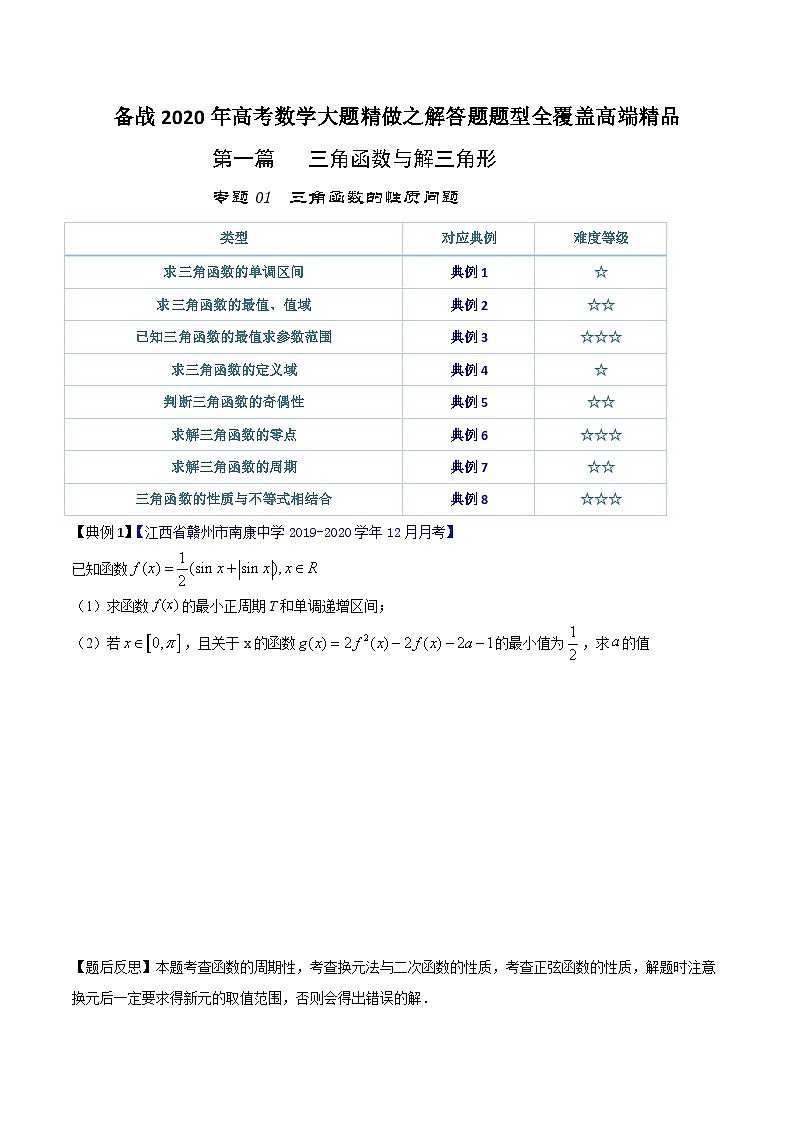
专题01 三角函数的性质问题
【典例1】【江西省赣州市南康中学2019-2020学年12月月考】
已知函数
（1）求函数的最小正周期T和单调递增区间；
（2）若，且关于x的函数的最小值为，求的值
【题后反思】本题考查函数的周期性，考查换元法与二次函数的性质，考查正弦函数的性质，解题时注意换元后一定要求得新元的取值范围，否则会得出错误的解．
【典例2】【北京市西城区2019-2020学年高三上学期期末数学试题】
已知函数
（1）求函数的最小正周期;
（2）求函数在区间上的最小值和最大值.
分析：
（1）先利用两角差的正弦公式展开，再利用二倍角公式和辅助角公式(或两角差的正弦公式)合并成的形式，即可求出函数的最小正周期.
（2）由，求出，再根据的单调性可求出函数的最大最小值．
【题后反思】
本题主要考查两角差的正弦公式、二倍角公式、辅助角公式的应用，以及三角函数在闭区间上的最值求法，意在考查学生的转化和运算能力，属于基础题．
【典例3】
【北京市海淀区2019-2020学年高三上学期期末数学试题】
已知函数.
（Ⅰ）求函数的单调递增区间；
（Ⅱ）若在区间上的最大值为，求的最小值.
分析：
（Ⅰ）利用二倍角的降幂公式以及辅助角公式将函数的解析式变形为，然后解不等式，即可得出函数的单调递增区间；
（Ⅱ）由，，结合题意得出，即可求出实数的最小值.
【典例4】已知函数；
（1）求的定义域与最小正周期；
（2）求在区间上的单调性与最值.
【典例5】【2019年浙江省高考数学试卷】
设函数.
（1）已知函数是偶函数，求的值；
（2）求函数 的值域.
【典例6】【北京市首都师范大学附属中学2019届高三一模数学（理科)试题】
已知函数.
（Ⅰ）求函数的最小正周期和单调递增区间；
（Ⅱ）已知，是函数的两个零点，求的最小值.
分析：
（Ⅰ）利用两角和差的正弦公式以及三角函数的倍角公式，辅助角公式进行化简，结合周期公式，以及函数的单调性进行求解即可；（Ⅱ）根据零点求出的根，利用作差法进行求解即可.
【题后反思】
本题主要考查三角函数的图象和性质.利用两角和差的正弦公式以及辅助角公式进行化简，利用三角函数值的关系是解决本题的关键.
【典例7】【2020届北京市昌平区高三上学期期末数学试题】
已知函数其中.
（1）若函数的最小正周期为，求的值；
（2）若函数在区间上的最大值为，求的取值范围.
分析：
(1)利用倍角公式以及辅助角公式化简函数，根据周期公式求出的值；
(2)利用求出，结合正弦函数的性质列出不等式即可求解.
【典例8】【北京市朝阳区2019-2020学年高三上学期期末数学试题】
已知函数．
（1）求的最小正周期；
（2）求的单调递增区间；
（3）对于任意都有恒成立，求的取值范围．
分析：
（1）将函数进行化简，根据三角函数的周期公式即可求函数f（x）的最小正周期T；
（2）由三角函数的图象与性质即可求函数f（x）的单调递增区间；
（3）原问题等价于的最大值小于零.
【针对训练】
1. 【2020届重庆市北碚区高三上学期第一次诊断性考试数学试题】
已知函数
（1）求函数的单调增区间；
（2）将函数的图象向左平移个单位，再向下平移1个单位后得到函数的图象，当时，求函数的值域．
2. 【内蒙古呼和浩特市2019-2020学年高三上学期质量普查调研】
已知函数，.
（1）若是第二象限角，且，求的值；
（2）求的最大值，及最大值对应的的取值.
3. 【陕西省宝鸡中学、西安三中等五校2019-2020学年高三上学期第一次联考】已知函数.
（1）当时，求的单调递增区间；
（2）当，且时，的值域是，求，的值.
4. 【2020届湖北省黄冈市高三上学期期末数学（理)试题】
已知函数．
求的值；
求的最小正周期及单调增区间．
5. 【湖南省邵阳市2019-2020学年高三第一次联考数学（文)试题】
已知函数.
（1）求的单调递减区间；
（2）若在区间上的最小值为，求的最大值.
6. 设函数的最小正周期为．
（1）求的单调递增区间；
（2）当时，求方程的解集．
7. 已知函数.
（Ⅰ）求函数的最小正周期及其单调增区间;
（Ⅱ）当时,对任意不等式恒成立,求实数的取值范围.
8. 【辽宁省丹东市2019-2020学年高三总复习阶段测试理科数学试题】
设函数．
（1）若点是图象的一个对称中心，求；
（2）当时，取得最小值，求．
9. 【陕西省西安市2019-2020学年高三上学期11月月考数学试题】
已知函数，且.
（1）求的解析式；
（2）已知，若对任意的，总存在，使得成立，求的取值范围.
10. 【2018年全国普通高等学校招生统一考试文科数学（北京卷)】
已知函数.
（Ⅰ）求的最小正周期；
（Ⅱ）若在区间上的最大值为，求的最小值.
类型
对应典例
难度等级
求三角函数的单调区间
典例1
☆
求三角函数的最值、值域
典例2
☆☆
已知三角函数的最值求参数范围
典例3
☆☆☆
求三角函数的定义域
典例4
☆
判断三角函数的奇偶性
典例5
☆☆
求解三角函数的零点
典例6
☆☆☆
求解三角函数的周期
典例7
☆☆
三角函数的性质与不等式相结合
典例8
☆☆☆
备战2020年高考数学大题精做之解答题题型全覆盖高端精品
第一篇 三角函数与解三角形
专题01 三角函数的性质问题
【典例1】【江西省赣州市南康中学2019-2020学年12月月考】
已知函数
（1）求函数的最小正周期T和单调递增区间；
（2）若，且关于x的函数的最小值为，求的值
答案：解：（1）
则函数的周期，函数的增区间.
（2）
令可得
换元可得，对称轴为
【题后反思】本题考查函数的周期性，考查换元法与二次函数的性质，考查正弦函数的性质，解题时注意换元后一定要求得新元的取值范围，否则会得出错误的解．
【典例2】【北京市西城区2019-2020学年高三上学期期末数学试题】
已知函数
（1）求函数的最小正周期;
（2）求函数在区间上的最小值和最大值.
分析：
（1）先利用两角差的正弦公式展开，再利用二倍角公式和辅助角公式(或两角差的正弦公式)合并成的形式，即可求出函数的最小正周期.
（2）由，求出，再根据的单调性可求出函数的最大最小值．
【解析】
（1）因为
所以函数的最小正周期为．
（2）因为，所以，而在上单调递减，在上单调递增，而，
所以当，即时，取得最小值，
当，即时，取得最大值．
【题后反思】
本题主要考查两角差的正弦公式、二倍角公式、辅助角公式的应用，以及三角函数在闭区间上的最值求法，意在考查学生的转化和运算能力，属于基础题．
【典例3】
【北京市海淀区2019-2020学年高三上学期期末数学试题】
已知函数.
（Ⅰ）求函数的单调递增区间；
（Ⅱ）若在区间上的最大值为，求的最小值.
分析：
（Ⅰ）利用二倍角的降幂公式以及辅助角公式将函数的解析式变形为，然后解不等式，即可得出函数的单调递增区间；
（Ⅱ）由，，结合题意得出，即可求出实数的最小值.
【解析】
（Ⅰ），
因为的单调递增区间为，
令，得.
所以函数的单调递增区间为；
（Ⅱ）因为，所以.
又因为，的最大值为，
所以，解得，所以的最小值为.
【典例4】已知函数；
（1）求的定义域与最小正周期；
（2）求在区间上的单调性与最值.
【解析】
；
（1）的定义域：，最小正周期 ；
（2），即最大值为1，最小值为，单调递增：，单调递减：.
【典例5】【2019年浙江省高考数学试卷】
设函数.
（1）已知函数是偶函数，求的值；
（2）求函数 的值域.
【解析】
(1)由题意结合函数的解析式可得：，
函数为偶函数，则当时，，即，结合可取，相应的值为.
(2)由函数的解析式可得：
.
据此可得函数的值域为：.
【典例6】【北京市首都师范大学附属中学2019届高三一模数学（理科)试题】
已知函数.
（Ⅰ）求函数的最小正周期和单调递增区间；
（Ⅱ）已知，是函数的两个零点，求的最小值.
分析：
（Ⅰ）利用两角和差的正弦公式以及三角函数的倍角公式，辅助角公式进行化简，结合周期公式，以及函数的单调性进行求解即可；（Ⅱ）根据零点求出的根，利用作差法进行求解即可.
【解析】
（Ⅰ）
则函数的最小正周期
由，，得，
即函数的单调递增区间为，
（Ⅱ），是函数的两个零点
由得
则由得…①，…②
则②①得
即，
则，
则当时，取得最小值，最小值为
【题后反思】
本题主要考查三角函数的图象和性质.利用两角和差的正弦公式以及辅助角公式进行化简，利用三角函数值的关系是解决本题的关键.
【典例7】【2020届北京市昌平区高三上学期期末数学试题】
已知函数其中.
（1）若函数的最小正周期为，求的值；
（2）若函数在区间上的最大值为，求的取值范围.
分析：
(1)利用倍角公式以及辅助角公式化简函数，根据周期公式求出的值；
(2)利用求出，结合正弦函数的性质列出不等式即可求解.
【解析】
（1）因为
.
因为的最小正周期为，即
所以.
（2）因为，
所以.
若在区间上取到最大值，只需，
所以.
【典例8】【北京市朝阳区2019-2020学年高三上学期期末数学试题】
已知函数．
（1）求的最小正周期；
（2）求的单调递增区间；
（3）对于任意都有恒成立，求的取值范围．
分析：
（1）将函数进行化简，根据三角函数的周期公式即可求函数f（x）的最小正周期T；
（2）由三角函数的图象与性质即可求函数f（x）的单调递增区间；
（3）原问题等价于的最大值小于零.
【解析】
（1）因为，
.所以的最小正周期．
（2）由（1）知．
又函数的单调递增区间为(Z)．
由，，
得，．
所以的单调递增区间为.
（3）因为，所以.
所以.所以.
当，即时，的最大值为，
又因为对于任意恒成立，所以，即.
所以的取值范围是.
【针对训练】
1. 【2020届重庆市北碚区高三上学期第一次诊断性考试数学试题】
已知函数
（1）求函数的单调增区间；
（2）将函数的图象向左平移个单位，再向下平移1个单位后得到函数的图象，当时，求函数的值域．
答案：解：
．
（1）由，，
解得，．
∴函数的单调增区间为，；
（2）将函数的图象向左平移个单位，
得，
再向下平移1个单位后得到函数，
由，得，
∴，则函数的值域为
2. 【内蒙古呼和浩特市2019-2020学年高三上学期质量普查调研】
已知函数，.
（1）若是第二象限角，且，求的值；
（2）求的最大值，及最大值对应的的取值.
答案：解：
（1）
，，则，则，
∵是第二象限角，∴，∴.
（2）.
当时，取得最大值3，
此时，即.
3. 【陕西省宝鸡中学、西安三中等五校2019-2020学年高三上学期第一次联考】已知函数.
（1）当时，求的单调递增区间；
（2）当，且时，的值域是，求，的值.
分析：
（1）当时，利用降幂公式，和辅助角公式化简函数，再求函数的单调递增区间；
（2）类似于（1）的化简，先求的范围，再求的范围，再用表示函数的最值，列方程组求解.
【解析】
（1）当时，.
由得：，
所以的单调递增区间为；
（2）因为，
，
所以，，又的值域是，
所以，.
4. 【2020届湖北省黄冈市高三上学期期末数学（理)试题】
已知函数．
求的值；
求的最小正周期及单调增区间．
【解析】1因为，
所以；
（2）的最小正周期．
令，解得，
所以的单调增区间为．
5. 【湖南省邵阳市2019-2020学年高三第一次联考数学（文)试题】
已知函数.
（1）求的单调递减区间；
（2）若在区间上的最小值为，求的最大值.
【解析】（1）由题意知：
化简得：
当单调递减时，
解得：
即函数的单调递减区间为.
（2）当在区间上的最小值为时，存在，
使得，即，解得：，
则时，存在.
6. 设函数的最小正周期为．
（1）求的单调递增区间；
（2）当时，求方程的解集．
答案：解：
由已知，得故
（1）令，解得：，
的单调递增区间为，；
（2），，
，或，
即或，所以方程的解集为
7. 已知函数.
（Ⅰ）求函数的最小正周期及其单调增区间;
（Ⅱ）当时,对任意不等式恒成立,求实数的取值范围.
答案：解析：（Ⅰ）因为
函数的定义域为
,
所以的递增区间为
（Ⅱ）因为,所以当时,
所以恒成立,即恒成立,
①当时,显然成立;
②当时,若对于恒成立,只需成立,所以,
综上,的取值范围是
8. 【辽宁省丹东市2019-2020学年高三总复习阶段测试理科数学试题】
设函数．
（1）若点是图象的一个对称中心，求；
（2）当时，取得最小值，求．
【解析】（1），
是图象的一个对称中心，，
，可得，，
（2）由题意可得，，，①
时，取得最小值，时，取得极小值，
故，，，②
①②联立可得，，
9. 【陕西省西安市2019-2020学年高三上学期11月月考数学试题】
已知函数，且.
（1）求的解析式；
（2）已知，若对任意的，总存在，使得成立，求的取值范围.
分析：
（1）由,可求出的值,进而可求得的解析式;
（2）分别求得和的值域,再结合两个函数的值域间的关系可求出的取值范围.
【详解】
（1）因为,所以,
解得,
故.
（2）因为,所以,所以，则,
图象的对称轴是.
因为,所以,
则,解得,故的取值范围是.
10. 【2018年全国普通高等学校招生统一考试文科数学（北京卷)】
已知函数.
（Ⅰ）求的最小正周期；
（Ⅱ）若在区间上的最大值为，求的最小值.
【解析】
（Ⅰ），
所以的最小正周期为.
（Ⅱ）由（Ⅰ）知.
因为，所以.
要使得在上的最大值为，
即在上的最大值为1.
所以，即.
所以的最小值为.
题后反思：本题主要考查三角函数的有关知识，解题时要注意利用二倍角公式及辅助角公式将函数化简，化简时要注意特殊角三角函数值记忆的准确性，及公式中符号的正负.
类型
对应典例
难度等级
求三角函数的单调区间
典例1
☆
求三角函数的最值、值域
典例2
☆☆
已知三角函数的最值求参数范围
典例3
☆☆☆
求三角函数的定义域
典例4
☆
判断三角函数的奇偶性
典例5
☆☆
求解三角函数的零点
典例6
☆☆☆
求解三角函数的周期
典例7
☆☆
三角函数的性质与不等式相结合
典例8
☆☆☆