高考数学大题精做专题02求轨迹方程问题(第五篇)(原卷版+解析)

这是一份高考数学大题精做专题02求轨迹方程问题(第五篇)(原卷版+解析)，共17页。
专题02 求轨迹方程问题
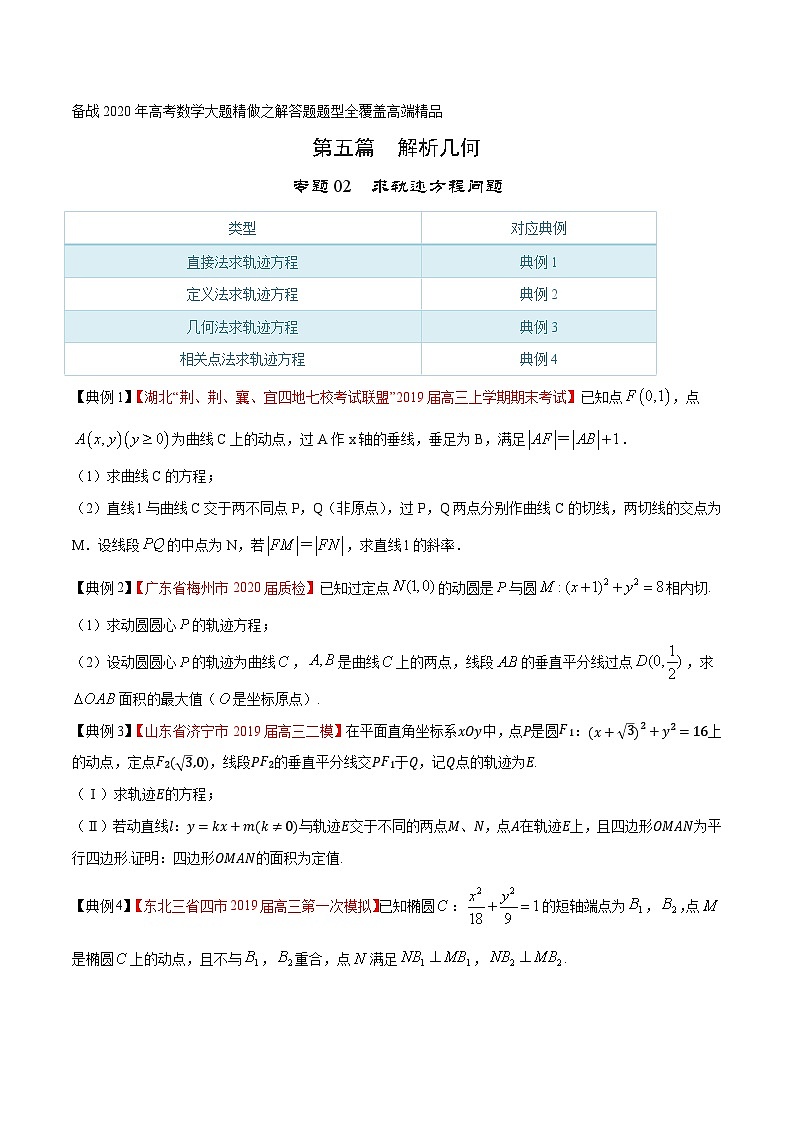
【典例1】【湖北“荆、荆、襄、宜四地七校考试联盟”2019届高三上学期期末考试】已知点，点为曲线C上的动点，过A作x轴的垂线，垂足为B，满足．
（1）求曲线C的方程；
（2）直线l与曲线C交于两不同点P，Q（非原点），过P，Q两点分别作曲线C的切线，两切线的交点为M．设线段的中点为N，若，求直线l的斜率．
【典例2】【广东省梅州市2020届质检】已知过定点的动圆是与圆相内切.
（1）求动圆圆心的轨迹方程；
（2）设动圆圆心的轨迹为曲线，是曲线上的两点，线段的垂直平分线过点，求面积的最大值（是坐标原点）.
【典例3】【山东省济宁市2019届高三二模】在平面直角坐标系xOy中，点P是圆F1：(x+3)2+y2=16上的动点，定点F2(3,0)，线段PF2的垂直平分线交PF1于Q，记Q点的轨迹为E.
（Ⅰ）求轨迹E的方程；
（Ⅱ）若动直线l：y=kx+m(k≠0)与轨迹E交于不同的两点M、N，点A在轨迹E上，且四边形OMAN为平行四边形.证明：四边形OMAN的面积为定值.
【典例4】【东北三省四市2019届高三第一次模拟】已知椭圆：的短轴端点为，，点是椭圆上的动点，且不与，重合，点满足，.
（Ⅰ）求动点的轨迹方程；
（Ⅱ）求四边形面积的最大值.
【针对训练】
1. 【广东省广州市2019届高三第二次模拟】从抛物线上任意一点P向x轴作垂线段，垂足为Q，点M是线段上的一点，且满足
(1)求点M的轨迹C的方程；
(2)设直线与轨迹c交于两点，T为C上异于的任意一点，直线，分别与直线交于两点，以为直径的圆是否过x轴上的定点？若过定点，求出符合条件的定点坐标；若不过定点，请说明理由．
2. 【陕西省咸阳市2020届高三模拟考试】已知圆的圆心为，点是圆上的动点，点，线段的垂直平分线交于点.
（I）求点的轨迹的方程；
（Ⅱ）过点作斜率不为0的直线与（I）中的轨迹交于，两点，点关于轴的对称点为，连接交轴于点，求.
【思路引导】
（1）利用待定系数法求出点在以、为焦点，长轴长为4的椭圆上，点的轨迹的方程为．（2）先求出点Q的坐标，再利用两点间的距离公式求．
3. 【陕西省延安市2019届高考模拟】已知两直线方程与，点在上运动，点在上运动，且线段的长为定值.
（Ⅰ）求线段的中点的轨迹方程；
（Ⅱ）设直线与点的轨迹相交于，两点，为坐标原点，若，求原点的直线的距离的取值范围.
4. 【江西省南昌市2020届模拟】如图，已知圆的方程为，圆的方程为，若动圆与圆内切与圆外切．
求动圆圆心的轨迹的方程；
过直线上的点作圆的两条切线，设切点分别是，若直线与轨迹交于两点，求的最小值．
类型
对应典例
直接法求轨迹方程
典例1
定义法求轨迹方程
典例2
几何法求轨迹方程
典例3
相关点法求轨迹方程
典例4
备战2020年高考数学大题精做之解答题题型全覆盖高端精品
第五篇 解析几何
专题02 求轨迹方程问题
【典例1】【湖北“荆、荆、襄、宜四地七校考试联盟”2019届高三上学期期末考试】已知点，点为曲线C上的动点，过A作x轴的垂线，垂足为B，满足．
（1）求曲线C的方程；
（2）直线l与曲线C交于两不同点P，Q（非原点），过P，Q两点分别作曲线C的切线，两切线的交点为M．设线段的中点为N，若，求直线l的斜率．
【思路引导】
（1）将坐标化，化简求得结果.
（2）设直线的方程为： ，与抛物线方程联立得，由韦达定理求得中点N的坐标，由导数的几何意义可求得过点的切线方程，联立求得交点的坐标，得到,所以MN中点纵坐标为1，即2，进而求得k.
【详解】
（1）由得：
化简得曲线的方程为.
（2）由题意可知直线l的斜率存在，
设直线的方程为：，联立得：
设，，则，
设，则，
又曲线的方程为，即y=,=，
∴过点的切线斜率为，切线方程为y-，即y=
同理，过点的切线方程为y=，
联立两切线可得交点的坐标为，
所以,又因为，所以MN中点纵坐标为1，即2
,k=,故直线的斜率为k=
【典例2】【广东省梅州市2020届质检】已知过定点的动圆是与圆相内切.
（1）求动圆圆心的轨迹方程；
（2）设动圆圆心的轨迹为曲线，是曲线上的两点，线段的垂直平分线过点，求面积的最大值（是坐标原点）.
【思路引导】
(1)由题易知，可得为定值，利用椭圆的定义求得结果；
(2)设所在直线方程为椭圆联立，表示出AB的长度和到直线的距离，求得的面积，再由题k与b的关系，可得答案.
【详解】
解:(1)圆的圆心为,半径为,
设圆的半径为,由题意知点在圆内.
可得
所以点的轨迹是以,为焦点,长轴长为的椭圆,
得
所以动圆圆心的轨迹方程为
(2)显然不与轴垂直,设所在直线方程为可得
可得……①设,
则是方程①的两不相等的实根,得

得
又点到直线的距离
所以的面积
由题意知,
得
又
代入上式得
得
(也可直接用垂直平分线过点得到关系)
当时,
当时,有最大值
当时,
当时,有最大值
所以面积的最大值为
【典例3】【山东省济宁市2019届高三二模】在平面直角坐标系xOy中，点P是圆F1：(x+3)2+y2=16上的动点，定点F2(3,0)，线段PF2的垂直平分线交PF1于Q，记Q点的轨迹为E.
（Ⅰ）求轨迹E的方程；
（Ⅱ）若动直线l：y=kx+m(k≠0)与轨迹E交于不同的两点M、N，点A在轨迹E上，且四边形OMAN为平行四边形.证明：四边形OMAN的面积为定值.
【思路引导】
(Ⅰ)由题意利用图形的几何性质和椭圆的定义即可确定轨迹方程；
(Ⅱ)联立直线方程与(Ⅰ)中求得的轨迹方程，结合韦达定理和平行四边形的性质得到面积的表达式，进一步计算即可证得其面积为定值.
【详解】
（Ⅰ）由题意：QF1+QF2=PF1=4，
∴根据椭圆的定义，点Q的轨迹E是以F1、F2为焦点的椭圆，其中2a=4，2c=23.
∴a=2，c=3，b2=a2−c2=4−3=1，
∴轨迹E的方程为：x24+y2=1；
（Ⅱ）证明：设M(x1,y1)、N(x2,y2)，
联立方程组x24+y2=1y=kx+m，得1+4k2x2+8kmx+4m2−4=0，
Δ=(8km)2−41+4k24m2−4>0，∴m2