高考数学大题精做专题08立体几何中线段与面积等求解问题(第三篇)(原卷版+解析)

这是一份高考数学大题精做专题08立体几何中线段与面积等求解问题(第三篇)(原卷版+解析)，共16页。
专题08 立体几何中线段与面积等求解问题
【典例1】【四川省宜宾市2019届高三上学期第一次诊断测试】
在如图所示的几何体中，已知，平面ABC，，，若M是BC的中点，且，平面PAB．
求线段PQ的长度；
求三棱锥的体积V．
【典例2】【山东、湖北部分重点中学2020届模拟】
如图，五边形中，四边形为长方形，三角形为边长为2的正三角形，将三角形沿折起，使得点在平面上的射影恰好在上.
（1）当时，证明：平面平面；
（2）当时，求四棱锥的侧面积.
【典例3】【河南省焦作市2019届高三年级第四次模拟考试】
如图，在三棱柱中，底面为正三角形，底面，，点在线段上，平面平面.
（1）请指出点的位置，并给出证明；
（2）若，求点到平面的距离.
【针对训练】
1. 【2020届北京市房山区高三模拟】
如图，三棱柱ABC−A1B1C1中，AA1⊥平面ABC，∠ACB=90°，AC=BC=1，AA1=2，以AB，BC为邻边作平行四边形ABCD，连接DA1和DC1.
（Ⅰ）求证：A1D∥平面BCC1B1；
（Ⅱ）求直线CC1与平面DA1C1所成角的正弦值；
（Ⅲ）线段BC上是否存在点F，使平面DA1C1与平面A1C1F垂直？若存在，求出BF的长；若不存在，说明理由.
2．【2020届重庆市高三学业质量调研】
如图所示，在长方体ABCD−A1B1C1D1中，E,F,P,Q分别是BC,C1D1,AD1,BD的中点 .
（Ⅰ）求证：EF//平面BB1D1D；
（Ⅱ）若AB=BB1=2a,AD=a，求点A到平面PDQ的距离.
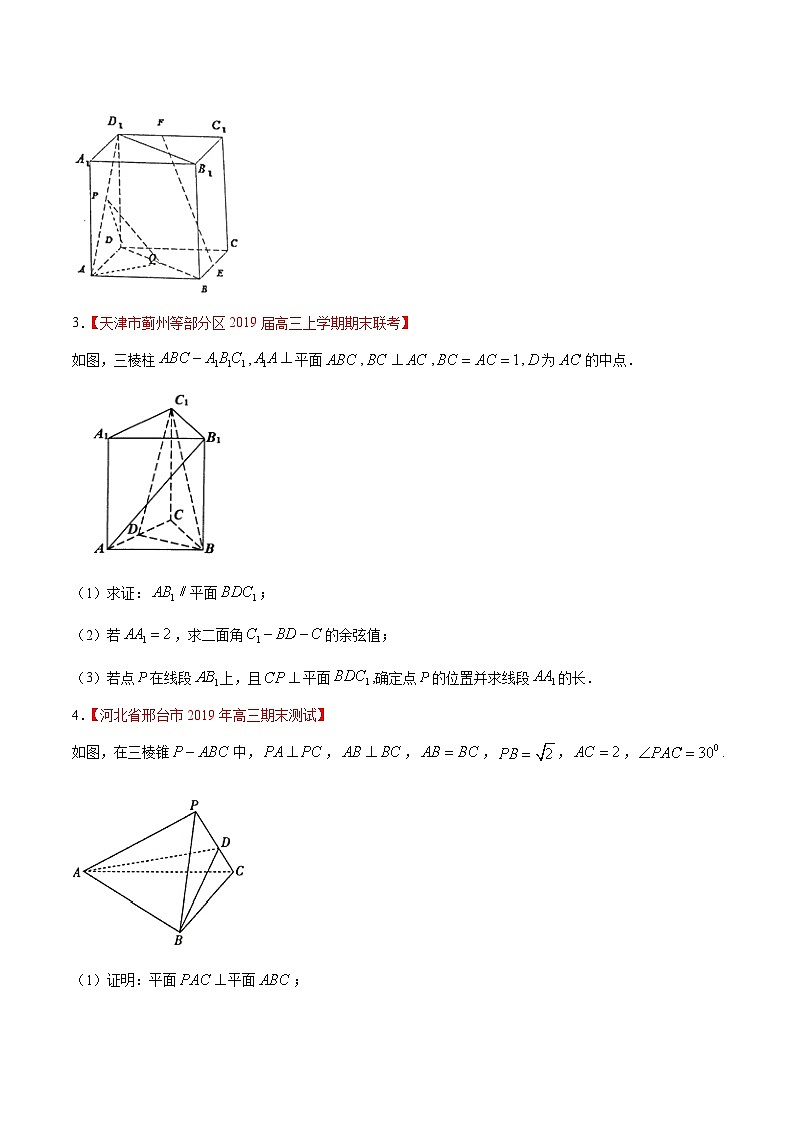
3．【天津市蓟州等部分区2019届高三上学期期末联考】
如图，三棱柱,平面,,,为的中点．
（1）求证：平面；
（2）若，求二面角的余弦值；
（3）若点在线段上，且平面,确定点的位置并求线段的长．
4．【河北省邢台市2019年高三期末测试】
如图，在三棱锥中，，，，，，.
（1）证明：平面平面；
（2）已知为棱上一点，若四面体的体积为，求线段的长.
5．【2019年全国统一高考数学试卷（文科)（新课标Ⅲ)】
图1是由矩形和菱形组成的一个平面图形，其中， ，将其沿折起使得与重合，连结，如图2.
（1）证明图2中的四点共面，且平面平面；
（2）求图2中的四边形的面积.
类型
对应典例
线段求解问题
典例1
面积求解问题
典例2
点到面的距离求解问题
典例3
备战2020年高考数学大题精做之解答题题型全覆盖高端精品
第三篇 立体几何
专题08 立体几何中线段与面积等求解问题
【典例1】【四川省宜宾市2019届高三上学期第一次诊断测试】
在如图所示的几何体中，已知，平面ABC，，，若M是BC的中点，且，平面PAB．
求线段PQ的长度；
求三棱锥的体积V．
【思路引导】
取AB的中点N，连接MN，PN，推导出四边形PQMN为平行四边形，由此能求出线段PQ的长度．
取AC的中点H，连接QH，推导出四边形PQHA为平行四边形，由此能求出三棱锥的体积．
解：取AB的中点N，连接MN，PN，
，且，
，、Q、M、N确定平面，
平面PAB，且平面平面，
又平面，，
四边形PQMN为平行四边形，
．
解：取AC的中点H，连接QH，
，且PQ=AH=2，四边形PQHA为平行四边形，
，平面ABC，平面ABC，
，，
三棱锥的体积：
．
【典例2】【山东、湖北部分重点中学2020届模拟】
如图，五边形中，四边形为长方形，三角形为边长为2的正三角形，将三角形沿折起，使得点在平面上的射影恰好在上.
（1）当时，证明：平面平面；
（2）当时，求四棱锥的侧面积.
【思路引导】
（Ⅰ）作，垂足为，平面，可得，
在中，.平面，由面面垂直的判定定理可得结果；(Ⅱ)可证明四个侧面有一个正三角形，一个等腰三角形，两个全等的直角三角形，分别求出特殊三角形的面积，然后求和即可.
试题解析：（Ⅰ）作，垂足为，依题意得平面，，
又，平面，.
利用勾股定理得，同理可得.
在中，
平面，又平面，
所以平面平面.
(Ⅱ)由（Ⅰ）中可知 ，同理，
，则由勾股定理可得，
，
中，，所以边上高 ，
，
，
所以四棱锥的侧面积.
【典例3】【河南省焦作市2019届高三年级第四次模拟考试】
如图，在三棱柱中，底面为正三角形，底面，，点在线段上，平面平面.
（1）请指出点的位置，并给出证明；
（2）若，求点到平面的距离.
【思路引导】
(1) 取中点为，的中点为，连接，，,通过几何关系得到四边形为平行四边形所以，再证，进而得到线面垂直，面面垂直；（2）由（1）可知，点到平面的距离为，由得到相应的点面距离.
【详解】
（1）点为线段的中点.
证明如下：取中点为，的中点为，连接，，.
所以，，所以四边形为平行四边形.所以.
因为，，所以.
又因为平面，平面，所以.
又，所以平面.
所以平面，而平面，所以平面平面.
（2）
由，得.由（1）可知，点到平面的距离为.
而的面积，，
等腰底边上的高为.
记点到平面的距离为，由 ，得，即点到平面的距离为.
【针对训练】
1. 【2020届北京市房山区高三模拟】
如图，三棱柱ABC−A1B1C1中，AA1⊥平面ABC，∠ACB=90°，AC=BC=1，AA1=2，以AB，BC为邻边作平行四边形ABCD，连接DA1和DC1.
（Ⅰ）求证：A1D∥平面BCC1B1；
（Ⅱ）求直线CC1与平面DA1C1所成角的正弦值；
（Ⅲ）线段BC上是否存在点F，使平面DA1C1与平面A1C1F垂直？若存在，求出BF的长；若不存在，说明理由.
【思路引导】
（1）要证明线面平行，需要在平面BCC1B1中找出一条直线平行于A1D.连结B1C，∵三棱柱ABC−A1B1C1中∴A1B1//AB且A1B1=AB，由平行四边形ABCD得CD//AB且CD=AB,
∴ A1B1//CD且A1B1=CD,∴四边形A1B1CD为平行四边形，A1D//B1C,∵ B1C⊂平面BCC1B1，A1D⊄平面BCC1B1,∴ A1D//平面BCC1B1.（2）建立空间直角坐标系，设平面DA1C1的法向量为n=(x,y,z)，利用n⋅A1D=0,n⋅A1C1=0.即x−2z=0y=0，令z=1，则y=0，x=2 ∴n=(2,0,1)，∴sinθ=|CC1⋅n||CC1|⋅|n|=22×5=55，∴直线CC1与平面DA1C1所成角的正弦值为55. （3）设F(λ,1,0)，−1≤λ≤0，则C1F=(λ,0,−2)，设平面A1C1F的法向量为，利用垂直关系A1C1⋅m=0C1F⋅m=0， 即y1=0λx1−2z1=0，令x1=1，则y1=0，z1=λ2，所以m=(1,0,λ2)，因为平面DA1C1的法向量为n=(2,0,1)，假设平面DA1C1与平面A1C1F垂直，则n⋅m=0，解得，λ=−4