第18讲 重难点专项突破04二次函数综合之“特殊四边形存在性”问题-初中人教版八升九数学暑假衔接（教师版+学生版）

这是一份第18讲 重难点专项突破04二次函数综合之“特殊四边形存在性”问题-初中人教版八升九数学暑假衔接（教师版+学生版），文件包含第18讲重难点专项突破04二次函数综合之“特殊四边形存在性”问题教师版-八升九数学暑假衔接人教版docx、第18讲重难点专项突破04二次函数综合之“特殊四边形存在性”问题学生版-八升九数学暑假衔接人教版docx等2份试卷配套教学资源，其中试卷共112页， 欢迎下载使用。
一、平行四边形的存在性问题
1.要先明确定点和动点，常以定点为对角线和边进行分类;
2.三定一动，有三种情况，可借助平移，全等、中点公式等知识确定坐标..(坐标平移规律:左减右加变x上加下减变 y如何平移?可先确定其中两点的变化作参照，以此变化确定)
3.两定两动:以定线段作边或对角线，确定分类;常借助对应边相等、坐标间关系及中点坐标公式建等式求解
常见设问:已知 A、B，求另外两点 C、D与A、B两点构成平行四边形
分类讨论:
当AB为边时，找AB平行且等于的 CD利用距离建立数量关系，求出相应点的坐标;
当AB为对角线时，AB 的中点即为对角线的交点，结合图形的对称性，围绕对角顶点的横坐标和纵坐标之和分别相等进行求解，列出两个二元一次方程组来求解.
4.三动点或四动点:往往有不变特征，如两边始终平行，满足相等即可
二、菱形的存在性问题(常为含 60°角的菱形)
通常有两大类:
1.已知三个定点探究菱形时，分别以三个定点中的任意两个定点确定线段为要探究的菱形的对角线画出
所有菱形，结合题干要求找出满足条件的菱形;
2已知两个定点去探究菱形时，以两个定点连线所成的线段作为要探究菱形的对角线或边长画出符合题意的
菱形，结合题干要求找出满足条件的菱形:
3.计算:建立类似平行四边形的存在性问题来解
三、矩形的存在性问题等价于直角三角形的存在性问题
（其特点往往是2定点2动点），通过构造一线三等角模型或勾股定理，可以求出其中一个顶点的坐标，再根据对称性求出另一个顶点的坐标。
分类的依据往往是以已知两点所在线段为边或对角线进行分类讨论。
四、正方形存在性问题
正方形是菱形和矩形特征的集结，因此同时采取菱形或矩形存在性问题解决的方法去求点的坐标。
【考点剖析】
题型一：平行四边形的存在性问题
1．（2023·广西贵港·统考三模）如图，抛物线与轴负半轴交于点，与轴交于A，两点，点A在点左侧，点的坐标为，．

(1)求抛物线的解析式；
(2)若点是第三象限抛物线上的动点，连接，当的面积为3时，求出此时点的坐标；
(3)将抛物线向右平移2个单位，平移后的抛物线与原抛物线相交于点，在原抛物线的对称轴上，为平移后的抛物线上一点，当以A、、、为顶点的四边形是平行四边形时，请直接写出点的坐标．
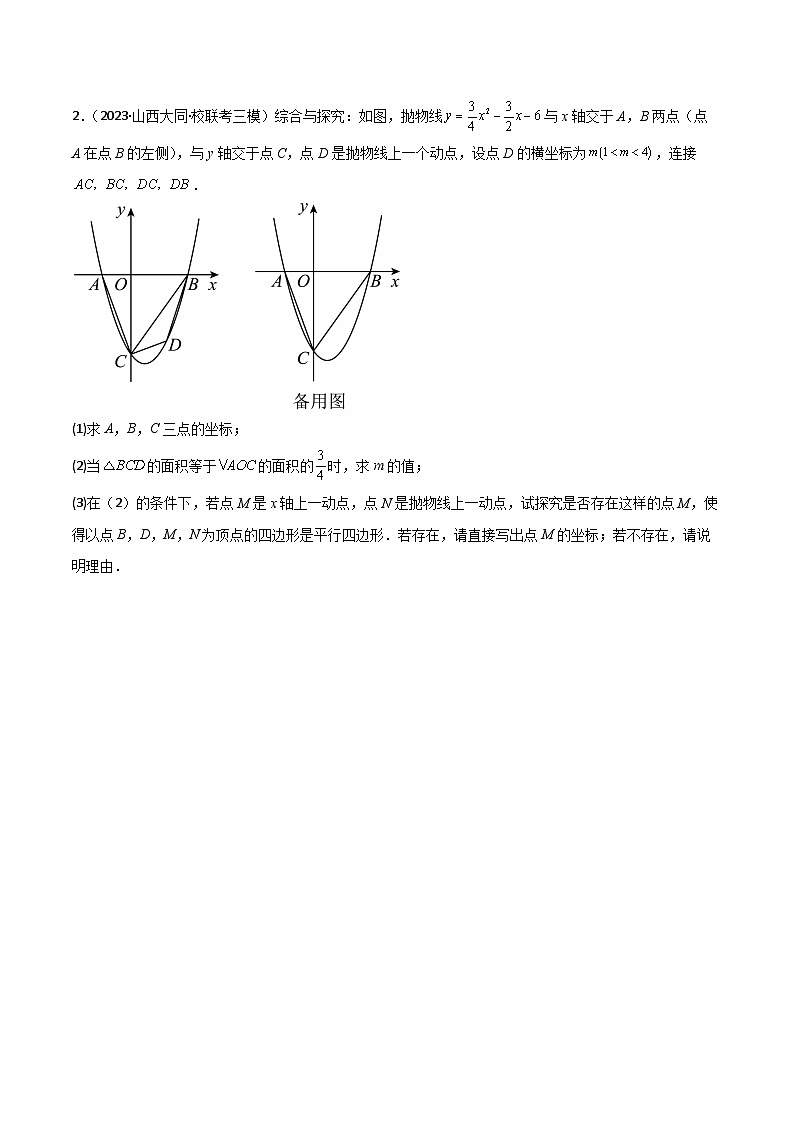
2．（2023·山西大同·校联考三模）综合与探究：如图，抛物线与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C，点D是抛物线上一个动点，设点D的横坐标为，连接．

(1)求A，B，C三点的坐标；
(2)当的面积等于的面积的时，求m的值；
(3)在（2）的条件下，若点M是x轴上一动点，点N是抛物线上一动点，试探究是否存在这样的点M，使得以点B，D，M，N为顶点的四边形是平行四边形．若存在，请直接写出点M的坐标；若不存在，请说明理由．
3．（2023·四川南充·统考中考真题）如图1，抛物线（）与轴交于，两点，与轴交于点．
(1)求抛物线的解析式；
(2)点P在抛物线上，点Q在x轴上，以B，C，P，Q为顶点的四边形为平行四边形，求点P的坐标；
(3)如图2，抛物线顶点为D，对称轴与x轴交于点E，过点的直线（直线除外）与抛物线交于G，H两点，直线，分别交x轴于点M，N．试探究是否为定值，若是，求出该定值；若不是，说明理由．
题型二：菱形的存在性问题
4．（2023·四川达州·统考中考真题）如图，抛物线过点．

(1)求抛物线的解析式；
(2)设点是直线上方抛物线上一点，求出的最大面积及此时点的坐标；
(3)若点是抛物线对称轴上一动点，点为坐标平面内一点，是否存在以为边，点为顶点的四边形是菱形，若存在，请直接写出点的坐标；若不存在，请说明理由．
5．（2023·山东日照·日照市新营中学校考三模）如图1，在平面直角坐标系中，抛物线与x轴交于和，与y轴交于点C，连接．

(1)求该抛物线的解析式；
(2)如图1，在x轴上有一动点D，平面内是否存在一点E，使以点A、D、C、E为顶点的四边形是菱形？若存在，请求出点E的坐标，若不存在，请说明理由．
(3)如图2，点M为抛物线上的一动点：
①若点M为直线上方的抛物线上任意一点，过点M作y轴的平行线，交于点N，过点M作x轴的平行线，交直线于点Q，求周长的最大值；
②若点M为抛物线上的任意一动点，且，请直接写出满足条件的点M的坐标．
6．（2023·四川广安·统考中考真题）如图，二次函数的图象交轴于点，交轴于点，点的坐标为，对称轴是直线，点是轴上一动点，轴，交直线于点，交抛物线于点．

(1)求这个二次函数的解析式．
(2)若点在线段上运动（点与点、点不重合），求四边形面积的最大值，并求出此时点的坐标．
(3)若点在轴上运动，则在轴上是否存在点，使以、为顶点的四边形是菱形？若存在，请直接写出所有满足条件的点的坐标；若不存在，请说明理由．
题型三：矩形的存在性问题
7．（2023春·辽宁阜新·九年级阜新实验中学校考阶段练习）如图，抛物线经过点，，．

(1)求抛物线的表达式；
(2)若点为第一象限内抛物线上的一点，设的面积为S，求S的最大值及此时点的坐标；
(3)已知是抛物线对称轴上一点，在平面内是否存在点，使以、、、为顶点的四边形是矩形？若存在，直接写出点坐标；若不存在，请说明理由．
8．（2023·山东东营·东营市胜利第一初级中学校考三模）已知抛物线交x轴于点和点，交y轴于点C．

(1)求抛物线的解析式；
(2)如图，点P是抛物线上位于直线下方的动点，过点P分别作x轴、y轴的平行线，交直线于点D，交x轴于点E，当取最大值时，求点P的坐标及最大值．
(3)在抛物线上是否存在点M，对于平面内任意点N，使得以A、C、M、N为顶点且为一条边的四边形为矩形，若存在，请直接写出M、N的坐标，不存在，请说明理由．
9．（2023·吉林松原·校联考三模）如图，抛物线过点，，点为x轴上一个动点（点M不与点A，C重合），过点M作垂直于x轴的直线与直线和抛物线分别交于点D，N．

(1)求此抛物线的解析式；
(2)求当点D是线段的中点时m的值；
(3)当与的面积相等时，求点M的坐标；
(4)过点D作轴于E，过点N作轴于F．直接写出在矩形内部的抛物线当y随x增大而增大时m的取值范围．
题型四：正方形存在性问题
10．（2023·陕西西安·校考模拟预测）如图，已知拋物线与轴交于点与轴交于点．

(1)求的值及该抛物线的对称轴；
(2)若点在直线上，点是平面内一点．是否存在点，使得以点为顶点的四边形为正方形？若存在，请求出点的坐标；若不存在，请说明理由．
11．（2023·辽宁·统考中考真题）如图，抛物线与轴交于点和点，与轴交于点，点在抛物线上．

(1)求抛物线的解析式；
(2)点在第一象限内，过点作轴，交于点，作轴，交抛物线于点，点在点的左侧，以线段为邻边作矩形，当矩形的周长为11时，求线段的长；
(3)点在直线上，点在平面内，当四边形是正方形时，请直接写出点的坐标．
12．（2023·黑龙江绥化·统考中考真题）如图，抛物线的图象经过，，三点，且一次函数的图象经过点．

(1)求抛物线和一次函数的解析式．
(2)点，为平面内两点，若以、、、为顶点的四边形是正方形，且点在点的左侧．这样的，两点是否存在？如果存在，请直接写出所有满足条件的点的坐标：如果不存在，请说明理由．
(3)将抛物线的图象向右平移个单位长度得到抛物线，此抛物线的图象与轴交于，两点（点在点左侧）．点是抛物线上的一个动点且在直线下方．已知点的横坐标为．过点作于点．求为何值时，有最大值，最大值是多少？
【过关检测】
一、单选题
1．（2022·全国·九年级专题练习）如图，直线y＝x+2与y轴交于点A，与直线y=x交于点B，以AB为边向右作菱形ABCD，点C恰与点O重合，抛物线y＝（x﹣h）2+k的顶点在直线y＝﹣x上移动．若抛物线与菱形的边AB、BC都有公共点，则h的取值范围是（ ）
A．﹣2≤h≤B．﹣2≤h≤1C．﹣1≤h≤D．﹣1≤h≤
2．（2021·山东济南·统考二模）如图，直线与y轴交于点A，与直线交于点D，以为边向左作菱形，点C恰与原点O重合，抛物线的顶点在直线上移动．若抛物线与菱形的边、都有公共点，则h的取值范围是（ ）
A．B．C．D．
3．（2022秋·吉林松原·九年级校联考期中）如图，在平面直角坐标系中，正方形ABCD四个顶点的坐标分别为A（1，1）、B（1，2）、C（2，2）、D（2，1）．若抛物线y＝向下平移m个单位（m＞0）与正方形ABCD的边（包括四个顶点）有交点，则m的值不可能是（ ）
A．1B．3C．5D．7
4．（2021·全国·九年级专题练习）如图，OABC是边长为1的正方形，OC与x轴正半轴的夹角为15°，点B在抛物线y＝ax2（a＜0）的图象上，则a的值为（ ）
A．B．C．﹣2D．
5．（2021春·九年级课时练习）如图，已知抛物线与x轴分别交于A、B两点，顶点为M．将抛物线l1沿x轴翻折后再向左平移得到抛物线l2．若抛物线l2过点B，与x轴的另一个交点为C，顶点为N，则四边形AMCN的面积为（ ）
A．32B．16C．50D．40
6．（2022·四川眉山·校考一模）如图，矩形OABC，点A的坐标为，AB＝1．若抛物线与矩形OABC的边界总有两个公共点，则实数c的取值范围是（ ）．
A．c＞8或c＜－1B．－1＜c＜8C．c＞1或c＜－8D．－8＜c＜1
7．（2022秋·福建南平·九年级统考期中）如图，在平面直角坐标系中，点A在抛物线上运动．过点A作轴于点C，以为对角线作矩形，连接，则对角线的最小值（ ）
A．0.5B．1C．1.5D．2
8．（2023·陕西西安·校考模拟预测）已知，抛物线L：（a和h都是常数，且）与x轴的一个交点为，顶点为C．将抛物线L绕点旋转，点A的对应点为，点C的对应点为．若四边形面积为8，则m的值为（ ）
A．3B．4C．5D．6
9．（2021·黑龙江大庆·统考一模）如图，直线与，轴分别交于点，，与直线交于点.，在线段上，动点以每秒1个单位长度的速度从点出发向点做匀速运动，过点作轴交直线于点，过点作轴交直线于点，轴于点，设运动时间为秒，四边形的面积为（点，重合除外），在运动过程中，当时，的值为（ ）
A．或B．或C．或D．或
10．（2023·浙江·九年级假期作业）如图，四边形是正方形，点E是线段上的动点，以为边作正方形，连接，M为的中点，且，则线段的最小值是( )

A．1B．C．D．2
二、填空题
11．（2023秋·河北承德·九年级统考期末）已知，，抛物线顶点在线段上运动，形状保持不变，与轴交于，两点（在的右侧），若时，四边形的形状为：________，此时点横坐标的最大值为：________．
12．（2023秋·九年级单元测试）如图，抛物线的顶点为，对称轴与轴交于点，当以为对角线的正方形的另外两个顶点、恰好在抛物线上时，我们把这样的抛物线称为“美丽抛物线”，正方形为它的内接正方形.
（1）当抛物线是“美丽抛物线”时，则________；当抛物线是“美丽抛物线”时，则________；
（2）若抛物线是“美丽抛物线”，则，之间的数量关系为________.
13．（2022秋·湖北黄冈·九年级校考期中）二次函数的图像如图，点位于坐标原点，点，，，…，在y轴的正半轴上，点，，，…，在二次函数位于第一象限的图像上，点，，，…，在二次函数位于第二象限的图像上，四边形，四边形，四边形，…，四边形都是菱形，，菱形的周长为______．
14．（2022秋·辽宁葫芦岛·九年级统考期中）如图所示，四边形的两条对角线，相互垂直，，则四边形的最大面积是___________．
15．（2022秋·浙江温州·九年级校考期中）如图，在平面直角坐标系中，正方形的顶点在轴正半轴上，顶点在轴的负半轴上，顶点在第四象限，已知点坐标为，以为顶点的抛物线恰好经过点，则的值为______．
16．（2022秋·甘肃陇南·九年级校考阶段练习）抛物线与直线围成的正方形有公共点，则实数的取值范围是___________．
17．（2023·福建宁德·统考模拟预测）已知抛物线的顶点为A，交y轴于点B；抛物线的顶点为C，交y轴于点D．若，且以A，B，C，D四点为顶点的四边形为矩形，则______．
18．（2023·新疆·模拟预测）如图，抛物线与交于点，且分别与轴交于点，．过点作轴的平行线，交抛物线于点，．则以下结论：
①无论取何值，总是负数；
②抛物线可由抛物线向右平移3个单位，再向下平移3个单位得到；
③当时，随着的增大，的值先增大后减小；
④四边形为正方形．
其中正确的是__________．（填写正确的序号）
三、解答题
19．（2023·宁夏银川·校考二模）如图，抛物线与轴交于，两点，过点的直线交抛物线于点．

(1)求抛物线的解析式．
(2)点是线段上一个动点，过点作轴的垂线交抛物线于点，求线段最大时点的坐标．
(3)点是抛物线上的动点，在轴的正半轴上是否存在点，使得以点，，，为顶点的四边形是平行四边形？如果存在，请直接写出所有满足条件的点的坐标；如果不存在，请说明理由．
20．（2023·江苏连云港·连云港市新海实验中学校考三模）如图1，平面直角坐标系中，抛物线与x轴分别交于点和点，与y轴交于点C，P为抛物线上一动点．

(1)写出抛物线的对称轴为直线______，抛物线的解析式为______；
(2)如图2，连结，若P在上方，作轴交于Q，把上述抛物线沿射线的方向向下平移，平移的距离为h，在平移过程中，该抛物线与直线始终有交点，求h的最大值；
(3)若P在上方，设直线，与抛物线的对称轴分别相交于点F，E，请探索以A，F，B，G（G是点E关于x轴的对称点）为顶点的四边形面积是否随着P点的运动而发生变化，若不变，求出这个四边形的面积；若变化，说明理由．
(4)设M为抛物线对称轴上一动点，当P，M运动时，在坐标轴上是否存在点N，使四边形为矩形？若存在，直接写出点P的横坐标；若不存在，请说明理由．
21．（2023·陕西西安·校考二模）已知抛物线经过点，，顶点为．
(1)求抛物线的表达式及顶点的坐标；
(2)将抛物线平移得到抛物线，点的对应点为，点的对应点为，点的对应点为，当以、、、为顶点的四边形是面积为20的菱形，且点在轴右侧时，求平移后得到的抛物线的表达式．
22．（2023秋·广东惠州·九年级统考期末）如下图，已知抛物线的顶点坐标为，且与轴交于点，与轴交于两点（点在点的右侧），点是抛物线上的一动点，从点沿抛物线向点运动（点与不重合），过点作轴，交于点．

(1)求该抛物线的函数关系式及点的坐标；
(2)求点在运动的过程中，线段的最大值；
(3)若点与点重合，点在轴上，点在抛物线上，当以为顶点的四边形为平行四边形时，直接写出点的坐标．
23．（2023·四川巴中·统考中考真题）在平面直角坐标系中，抛物线经过点和，其顶点的横坐标为．

(1)求抛物线的表达式．
(2)若直线与轴交于点，在第一象限内与抛物线交于点，当取何值时，使得有最大值，并求出最大值．
(3)若点为抛物线的对称轴上一动点，将抛物线向左平移个单位长度后，为平移后抛物线上一动点．在（）的条件下求得的点，是否能与、、构成平行四边形？若能构成，求出点坐标；若不能构成，请说明理由．
24．（2023·广东佛山·统考三模）如图，抛物线交直线于坐标轴上两点，交轴于另一点，连接．

(1)求抛物线的解析式；
(2)点为线段上一点，过点作直线，交轴于点．连接，求面积的最大值；
(3)若在直线上存在点，使得以点为顶点的四边形为菱形，求点的坐标．
25．（2023·山东枣庄·统考中考真题）如图，抛物线经过两点，并交x轴于另一点B，点M是抛物线的顶点，直线AM与轴交于点D．

(1)求该抛物线的表达式；
(2)若点H是x轴上一动点，分别连接MH，DH，求的最小值；
(3)若点P是抛物线上一动点，问在对称轴上是否存在点Q，使得以D，M，P，Q为顶点的四边形是平行四边形？若存在，请直接写出所有满足条件的点Q的坐标；若不存在，请说明理由．