



第01讲 三角形的边-人教版初中七年级(七升八)数学暑假衔接(教师版+学生版)讲义
展开一.三角形
(1)三角形的概念:由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.
组成三角形的线段叫做三角形的边.
相邻两边的公共端点叫做三角形的顶点.
相邻两边组成的角叫做三角形的内角,简称三角形的角.
(2)按边的相等关系分类:不等边三角形和等腰三角形(底和腰不等的等腰三角形、底和腰相等的等腰三角形即等边三角形).
二.三角形三边关系
(1)三角形三边关系定理:三角形两边之和大于第三边.
(2)在运用三角形三边关系判定三条线段能否构成三角形时并不一定要列出三个不等式,只要两条较短的线段长度之和大于第三条线段的长度即可判定这三条线段能构成一个三角形.
(3)三角形的两边差小于第三边.
(4)在涉及三角形的边长或周长的计算时,注意最后要用三边关系去检验,这是一个隐藏的定时炸弹,容易忽略.
【考点剖析】
一、三角形的识别与有关概念
一、单选题
1.(2020秋·浙江宁波·八年级校考期中)一位同学用三根木棒两两相交拼成如下图形,则其中符合三角形概念的是( )
A.B.
C.D.
2.(2022秋·广东惠州·八年级阶段练习)在△ABC中,BC边的对角是( )
A.∠AB.∠BC.∠CD.∠D
二、填空题
3.(2022秋·八年级课时练习)由不在同一条直线上的三条线段___________所组成的图形叫做三角形.
4.(2022秋·山西大同·八年级统考期中)一个三角形的两条边长分别为3,5,周长为11,那么它的第三边长为__________.
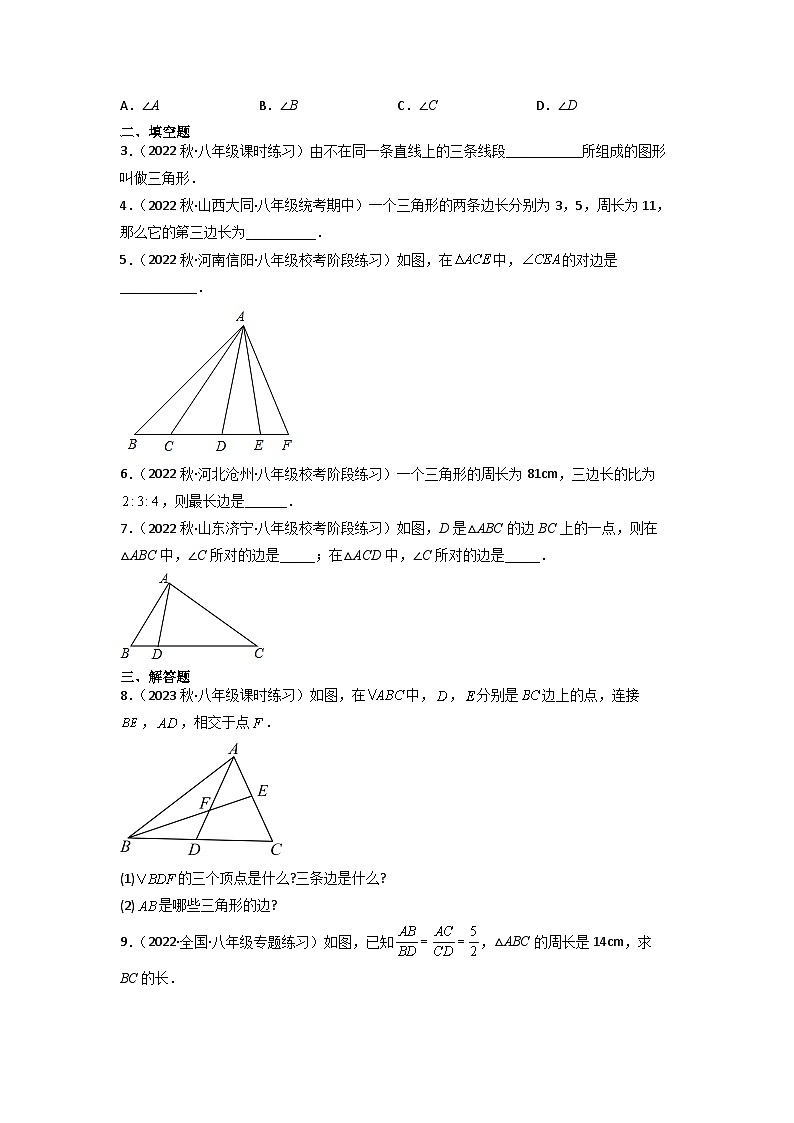
5.(2022秋·河南信阳·八年级校考阶段练习)如图,在中,的对边是___________.
6.(2022秋·河北沧州·八年级校考阶段练习)一个三角形的周长为81cm,三边长的比为,则最长边是______.
7.(2022秋·山东济宁·八年级校考阶段练习)如图,D是△ABC的边BC上的一点,则在△ABC中,∠C所对的边是_____;在△ACD中,∠C所对的边是_____.
三、解答题
8.(2023秋·八年级课时练习)如图,在中,,分别是边上的点,连接,,相交于点.
(1)的三个顶点是什么?三条边是什么?
(2)是哪些三角形的边?
9.(2022·全国·八年级专题练习)如图,已知,△ABC的周长是14cm,求BC的长.
二、三角形个数问题
一、单选题
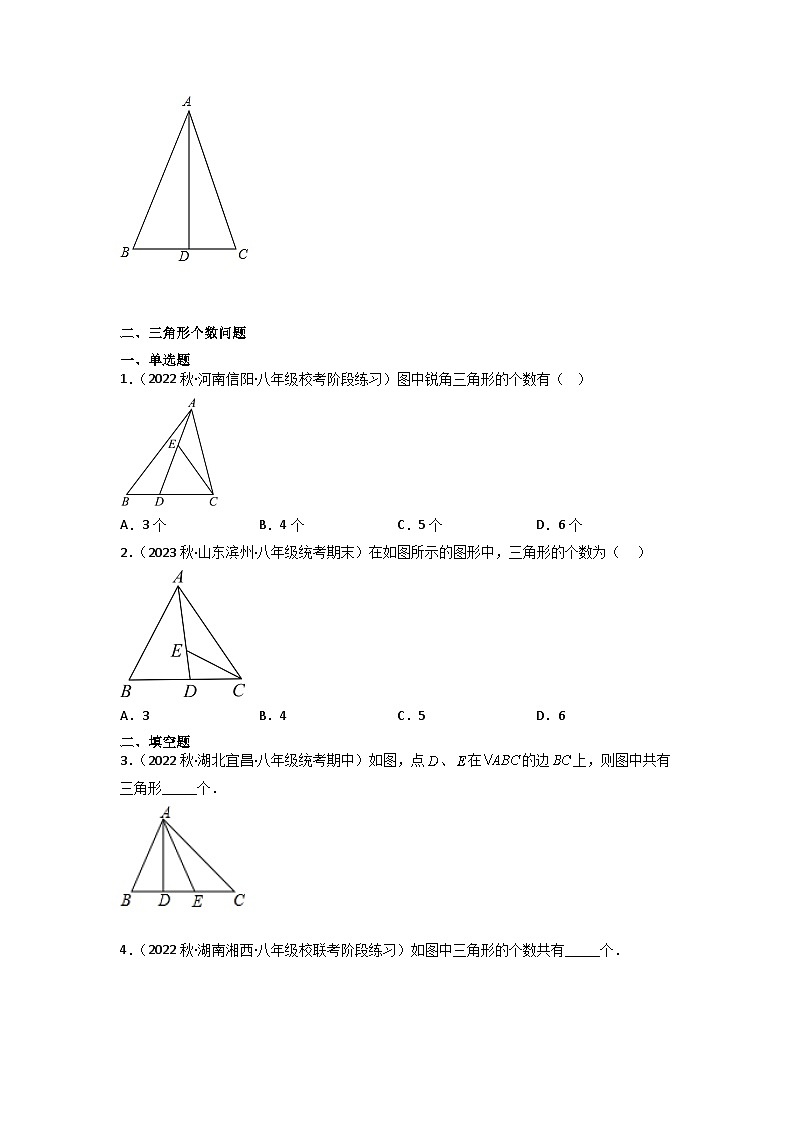
1.(2022秋·河南信阳·八年级校考阶段练习)图中锐角三角形的个数有( )
A.3个B.4个C.5个D.6个
2.(2023秋·山东滨州·八年级统考期末)在如图所示的图形中,三角形的个数为( )
A.3B.4C.5D.6
二、填空题
3.(2022秋·湖北宜昌·八年级统考期中)如图,点、在的边上,则图中共有三角形_____个.
4.(2022秋·湖南湘西·八年级校联考阶段练习)如图中三角形的个数共有_____个.
5.(2022秋·湖北恩施·八年级校考阶段练习)如图,一共有_________个三角形;从大小判断,图中青蛙可以落在个三角形内,则________.
6.(2022秋·广西百色·八年级统考期中)如图所示的三角形共有___________个.
7.(2022·全国·八年级专题练习)观察图形规律:
(1)图①中一共有________个三角形,图②中共有________个三角形,图③中共有________个三角形.
(2)由以上规律进行猜想,第n个图形共有________个三角形.
8.(2022秋·全国·八年级专题练习)若有一条公共边的两个三角形称为一对“共边三角形”,则图中以为公共边的“共边三角形”有___________对.
三、解答题
9.(2020秋·八年级课时练习)如图所示,图中共有多少个三角形?请写出这些三角形并指出所有以E为顶点的角.
10.(2022秋·全国·八年级专题练习)如图所示,
(1)图中有几个三角形?
(2)说出的边和角.
(3)是哪些三角形的边?是哪些三角形的角?
11.(2020秋·八年级课时练习)如图,在中,为AC边上不同的n个点,首先连接,图中出现了3个不同的三角形,再连接,图中便有6个不同的三角形……
(1)完成下表:
(2)若出现了45个三角形,则共连接了多少个点?
(3)若一直连接到,则图中共有多少个三角形?
三、三角形的分类
一、单选题
1.(2022秋·全国·八年级专题练习)用集合来表示“按边把三角形分类”,下面集合正确的是( )
A.B.
C.D.
2.(2022秋·河北邢台·八年级校考期中)如图表示三角形的分类,则表示的是( )
A.锐角三角形B.直角三角形C.钝角三角形D.三边都不相等的三角形
3.(2022·全国·八年级专题练习)图中的三角形被木板遮住了一部分,那么这个三角形是( )
A.锐角三角形B.直角三角形C.钝角三角形D.以上都有可能
4.(2022秋·山东德州·八年级校考阶段练习)一个三角形的三边长之比是2:2:1,周长是,此三角形按边分是( )
A.等腰三角形B.等边三角形C.不等边三角形D.以上都不对
二、填空题
5.(2022秋·八年级课时练习)________的三角形叫做直角三角形,记作________.
6.(2023秋·重庆忠县·八年级统考期末)在中,若,则的形状是_________三角形(填钝角、直角和锐角).
三、解答题
7.(2022秋·全国·八年级专题练习)已知的三边长分别为a,b,c.若a,b,c满足,试判断的形状.
8.(2022秋·广东湛江·八年级统考期末)如图,每个小正方形的边长均为1,点A和点B在小正方形的格点上.
(1)在图①中画出,使为直角三角形(要求点C在小正方形的格点上,画一个即可).
(2)求图①中的面积.
9.(2022秋·八年级课时练习)说出图中的锐角三角形,直角三角形和钝角三角形.
10.(2022秋·辽宁抚顺·八年级统考期中)图①、图②、图③均是的正方形网格,每个小正方形的边长为1,每个小正方形的顶点称为格点,线段的端点均在格点上,只用无刻度的直尺,在给定的网格中,按下列要求以为边画.
要求:
(1)在图①中画一个钝角三角形,在图②中画一个直角三角形,在图③中画一个锐角三角形;
(2)三个图中所画的三角形的面积均不相等;
(3)点在格点上.
11.(2022秋·全国·八年级专题练习)满足下列条件的三角形是锐角三角形、直角三角形还是钝角三角形.
(1)△ABC中,∠A=30°,∠C=∠B;
(2)三个内角的度数之比为1:2:3.
四、构成三角形的条件
一、单选题
1.(2022秋·福建南平·八年级福建省南平第一中学校考期中)以下列长度的三条线段为边,能组成三角形的是( )
A.1,3,3B.1,2,4C.1,2,3D.2,3,7
2.(2022秋·安徽六安·八年级统考期末)下列长度的三条线段,不能组成三角形的是( )
A.5,6,10B.三条线段之比为:
C.30,8,10D.,,
二、填空题
3.(2022秋·安徽合肥·八年级统考期中)有4条线段的长度分别是和,选择其中能组成三角形的三条线段作三角形,则可作______个不同的三角形.
4.(2022秋·湖北黄冈·八年级统考期中)若等腰三角形的两边的长分别是、,则它的周长为___________.
5.(2021秋·河南许昌·八年级校考阶段练习)乐乐同学有两根长度为4cm,7cm的木棒,母亲节时他想自己动手给妈妈钉一个三角形相框,现有五根长度分别为3cm,6cm,10cm,12cm,15cm的木棒供他选择,他有_____种选择.
6.(2022秋·浙江·八年级专题练习)三角形的三边长分别是2,5,m,则|m﹣3|+|m﹣7|等于___.
三、解答题
7.(2022秋·山东聊城·八年级统考期中)已知a,b,c为三角形的三边,满足,且,求三角形周长.
8.(2022秋·八年级课时练习)四根木棒的长度分别为.从中取三根,使它们首尾顺次相接组成一个三角形.一共有多少种取法?把它们都列出来.
9.(2022秋·八年级课时练习)判断下列各组线段中,哪些首尾相接能组成三角形,哪些不能组成三角形,并说明理由.
(1)a=2.5cm,b=3cm,c=5cm;
(2)e=6.3cm,f=6.3cm,g=12.6cm.
五、确定三边的取值范围
一、解答题
1.(2022秋·八年级课时练习)两根木棒的长分别是和.要选择第三根木棒,将它们首尾相接钉成一个三角形.若第三根木棒的长为偶数,则第三根木棒长的取值情况有几种?
2.(2022秋·云南昭通·八年级统考期中)某市木材市场上的木棒规格与价格如下表:
小明的爷爷要做一个三角形的支架用来养兔子,在木材市场上已经购买了两根长度分别为和的木棒,还需要购买一根.
(1)有几根规格的木棒可供小明的爷爷选择?
(2)在能做成三角形支架的情况下,要求做成的三角形支架的周长为偶数,则小明的爷爷做三角形支架,买木棒一共花了多少元?
3.(2022秋·河南三门峡·八年级统考期中)如果一个三角形的一边长为9cm、另一边长为1cm,求:
(1)这个三角形的第三边的范围;
(2)当第三边长为奇数时,求三角形的周长.
4.(2022秋·广东惠州·八年级期中)三角形的两边分别为2cm和4cm,且周长为偶数,求第三边长.
5.(2022秋·安徽蚌埠·八年级统考期中)已知:中,,,,求的范围.
6.(2022秋·河北邢台·八年级校考阶段练习)已知△ABC的三边长分别为1,4,a,化简:.
7.(2022秋·四川自贡·八年级校考阶段练习)已知一个三角形的三边长分别为,化简:.
8.(2022·全国·八年级专题练习)若一个三角形的三边长分别是a,b,c,其中a和b满足方程,若这个三角形的周长为整数,求这个三角形的周长.
9.(2023春·广东佛山·八年级校考阶段练习)若三角形的三边长分别是2,x,10,且x是不等式的正整数解,求该三角形的周长.
六、三角形三边关系应用
一、单选题
1.(2023秋·重庆丰都·八年级统考期末)从长度为2、4、6、8的四条线段中,任意取出三条线段,能围成三角形的是( )
A.2,4,6B.2,4,8C.2,6,8D.4,6,8
2.(2022秋·浙江绍兴·八年级校考期中)已知,,若长为整数,则长为( )
A.3B.6C.3或6D.3或4或5或6
3.(2022秋·浙江嘉兴·八年级统考期末)四根木棒的长度分别为,,,.现从中取三根,使它们首尾顺次相接组成一个三角形.则这样的取法共有( )
A.1种B.2种C.3种D.4种
4.(2023秋·福建泉州·八年级统考期末)已知a、b、c为三角形的三条边长,设,则m的值( )
A.B.C.D.或
5.(2023秋·云南昆明·八年级统考期末)如图,为估计池塘岸边A、B的距离,小杰在池塘的一侧选取一点O,测得米,米,A、B间的距离可能是( )
A.4米B.12米C.16米D.22米
6.(2023秋·重庆南川·八年级统考期末)袁老师在课堂上组织学生用小棍摆三角形,小棍的长度有和四种规格,小朦同学已经取了和两根木棍,那么第三根木棍不可能取( )
A.B.C.D.
二、解答题
7.(2023秋·八年级课时练习)如图,在中,点在上,连接,点在上,连接,求证:.
8.(2022秋·江西赣州·八年级统考期末)已知a,b,c是三角形的三边长.
(1)化简;
(2)若,,,求(1)中式子的值.
9.(2023秋·安徽池州·八年级统考期末)已知a,b,c是的三边.
(1)化简;
(2)若a和b满足方程组,且c为偶数,求这个三角形的周长.
【过关检测】
一.选择题(共10小题)
1.(2022秋•东平县期末)图中的三角形被木板遮住了一部分,这个三角形是( )
A.锐角三角形B.直角三角形
C.钝角三角形D.以上都有可能
2.(2022秋•文登区期末)若长度分别为x,2,5的三条线段能组成一个三角形,则x的值可能是( )
A.1B.2C.5D.7
3.(2022秋•东营区校级月考)图中,以DE为边的三角形有( )
A.2个B.3个C.4个D.5个
4.(2020秋•江汉区校级期末)一个三角形的三边之比为2:3:3,最短边为6,则这个三角形的周长为( )
A.32B.24C.25D.36
5.(2023春•大渡口区校级期中)以下数据分别是3根小木棒的长度.用这3根小木棒的长度为边能搭成三角形的是( )
A.1cm,2cm,3cmB.5cm,5cm,10cm
C.5cm,7cm,14cmD.3cm,4cm,5cm
6.(2022秋•莱芜区期末)若一个三角形的两边长分别为3和8,则第三边长可能是( )
A.14B.10C.3D.2
7.(2022秋•竞秀区期末)如图,下列说法不正确的是( )
A.直线m,n相交于点PB.PA+PB>QA+QB
C.PA+PB<QA+QBD.直线m不经过点Q
8.(2022秋•顺庆区校级期末)已知a,b,c是三角形的三条边,则|a+b﹣c|﹣|c﹣a﹣b|的化简结果为( )
A.0B.2a+2bC.2cD.2a+2b﹣2c
9.(2022秋•乳山市期中)如图,为估计池塘两岸A,B间的距离,小明在池塘一侧选取点M,测得MA=15m,MB=11m,那么AB间的距离不可能是( )
A.5mB.15mC.28mD.20m
10.(2022秋•招远市期中)有四根细木棒,长度分别为6cm,7cm,9cm,14cm,从中取三根木棒组成一个三角形,有_____种可能情况.( )
A.1B.2C.3D.4
二.填空题(共8小题)
11.(2022秋•泰山区校级月考)图中共有三角形 个.
12.(2023春•沈北新区期中)已知△ABC中,AB=5,AC=6,则BC的取值范围是 .
13.(2019秋•莱西市期中)如图所示,图中共有三角形 个.
14.(2022秋•南康区校级月考)图中共有三角形 个,其中以AE为边的三角形有 个.
15.(2022春•涟水县校级月考)如图,共有 个三角形.
16.(2022秋•龙口市期中)已知三角形的两边长分别为2和4,设第三边长为x,若x为整数,则适合的x值为 .(写出一个即可)
17.(2023春•上海期中)一个三角形的两边长分别是4和7,如果第三边长为整数,那么第三边可取的最大整数是 .
18.(2021秋•东平县期末)若a、b、c为三角形的三边长,且a、b满足|a﹣3|+(b﹣2)2=0,则第三边长c的取值范围是 .
三.解答题(共7小题)
19.图中有多少个三角形?
20.(2022秋•禹城市期中)已知三角形的两边长为8和10,第三边长x最小.
(1)求x的取值范围;
(2)当x为何值时,围成的三角形周长最大?并求出周长.
21.(2022秋•红花岗区期中)已知a,b,c是三角形的三边长.
(1)化简:|a﹣b﹣c|+|b﹣c﹣a|+|c﹣a﹣b|;
(2)若a=10,b=8,c=6,求(1)中式子的值.
22.如图,直线a上有5个点,A1,A2,…,A5,图中共有多少个三角形?
23.(2021秋•雁峰区期末)若一个三角形的三边长分别是a,b,c,其中a和b满足方程,若这个三角形的周长为整数,求这个三角形的周长.
24.(2018秋•静安区期末)如图,将三角形ABC沿射线BC平移后能与三角形DEF重合(点B、C分别与点E、F对应),如果BF的长为12,点E在边BC上,且2<EC<4,求边BC长的取值范围.
25.(2021秋•梁溪区期中)(1)如图1,图中共有三角形 个;如图2,若增加一条线,则图中共有三角形 个;
(2)如图3,若增加到10条线,请你求出图中的三角形的个数.
连接点的个数
1
2
3
4
5
6
出现三角形个数
规格
价格/(元/根)
第13讲 重难点01三角形中“8”字模型-人教版初中七年级(七升八)数学暑假衔接(教师版+学生版)讲义: 这是一份第13讲 重难点01三角形中“8”字模型-人教版初中七年级(七升八)数学暑假衔接(教师版+学生版)讲义,文件包含第13讲重难点01三角形中“8”字模型教师版-七升八数学暑假衔接人教版docx、第13讲重难点01三角形中“8”字模型学生版-七升八数学暑假衔接人教版docx等2份学案配套教学资源,其中学案共42页, 欢迎下载使用。
第12讲 角平分线的性-人教版初中七年级(七升八)数学暑假衔接(教师版+学生版)讲义: 这是一份第12讲 角平分线的性-人教版初中七年级(七升八)数学暑假衔接(教师版+学生版)讲义,文件包含第12讲角平分线的性质教师版-七升八数学暑假衔接人教版docx、第12讲角平分线的性质学生版-七升八数学暑假衔接人教版docx等2份学案配套教学资源,其中学案共69页, 欢迎下载使用。
第07讲 全等三角形-人教版初中七年级(七升八)数学暑假衔接(教师版+学生版)讲义: 这是一份第07讲 全等三角形-人教版初中七年级(七升八)数学暑假衔接(教师版+学生版)讲义,文件包含第07讲全等三角形教师版-七升八数学暑假衔接人教版docx、第07讲全等三角形学生版-七升八数学暑假衔接人教版docx等2份学案配套教学资源,其中学案共33页, 欢迎下载使用。












