湖南省永州市零陵区2023-2024学年八年级下学期期末数学试题

这是一份湖南省永州市零陵区2023-2024学年八年级下学期期末数学试题，共12页。试卷主要包含了本试卷包括试题卷和答题卡，下列说法正确的是等内容，欢迎下载使用。
温馨提示：
1．本试卷包括试题卷和答题卡．考生作答时，选择题和非选择题均须作答在答题卡上，在本试题卷上作答无效．考生在答题卡上按答题卡中注意事项的要求答题．
2．本试卷满分120分，考试时间120分钟．共26小题．如有缺页，考生须声明．
一、选择题（共10个小题，每小题3分，共30分，请将正确选项填涂到答题卡上）
1．中国“二十四节气”已被正式列入联合国教科文组织人类非物质文化遗产代表作品录，下列四幅作品分别代表“谷雨”、“大雪”、“小满”、“立夏”，其中是中心对称图形的是（ ）
A． B． C． D．
2．在平面直角坐标系中，已知y轴上一点P到x轴的距离是2，则点P的坐标是（ ）
A．（0，2）或（0，） B．（2，0） C．（，0） D．（，0）或（2，0）
3．如图，在下列给出的条件中，不能判定四边形ABCD为平行四边形的是（ ）
A．， B．，
C．， D．，
4．若是y关于x的一次函数，则其图象不经过（ ）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
5．下列说法正确的是（ ）
A．两个锐角对应相等的两个直角三角形全等 B．菱形既是轴对称图形又是中心对称图形
C．一次函数都是正比例函数 D．频数与频率相等
6．如图，在冷水滩区活龙井社区有一处小巷，其左右两侧是竖直的墙，一架梯子斜靠在左墙时，梯子底端到左墙的距离为0.7米，顶端距离地面2.4米．若保持梯子底端位置不动，将梯子斜靠在右墙时，顶端距离地面1.5米，则小巷的宽度为（ ）
A．1.8米 B．2米 C．2.5米 D．2.7米
7．如图，李明利用所学的数学知识，给同桌出了这样一道题：某人从点A出发，沿直线走6米后向左转θ，接着沿直线前进6米后，再向左转θ，…，如此下去，当他第一次回到点A时，发现自己一共走了48米，则θ的度数为（ ）
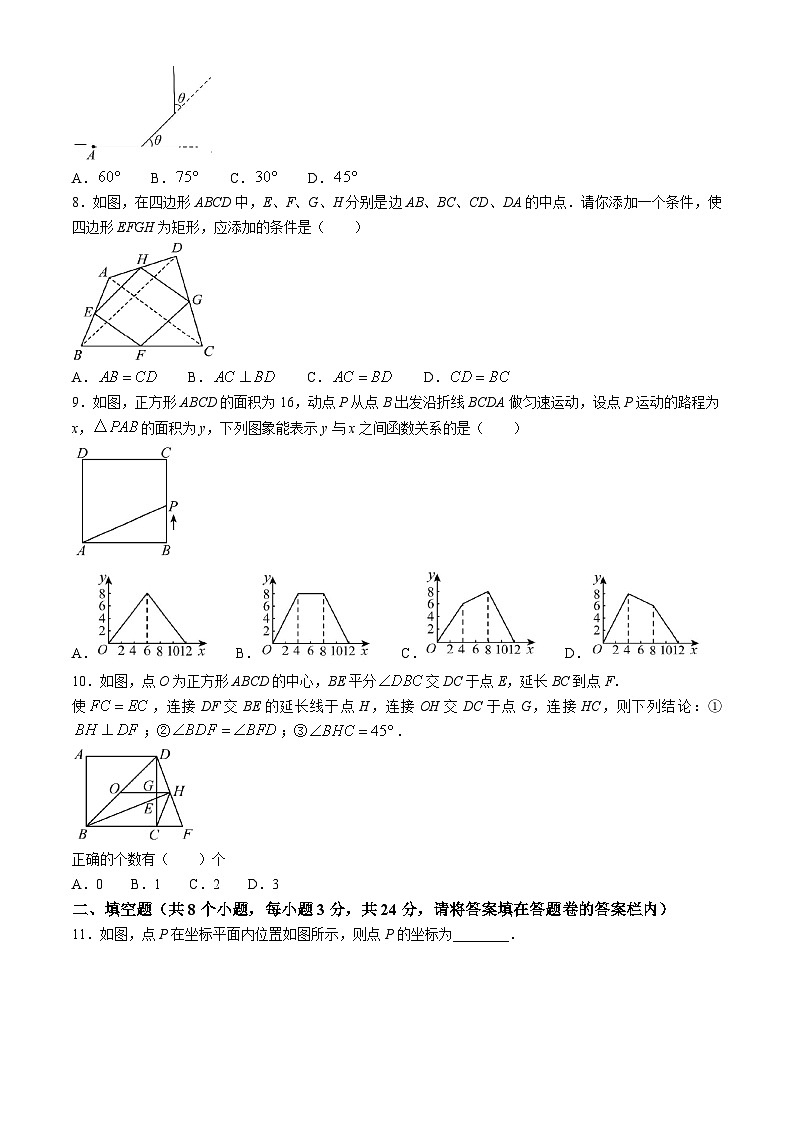
A． B． C． D．
8．如图，在四边形ABCD中，E、F、G、H分别是边AB、BC、CD、DA的中点．请你添加一个条件，使四边形EFGH为矩形，应添加的条件是（ ）
A． B． C． D．
9．如图，正方形ABCD的面积为16，动点P从点B出发沿折线BCDA做匀速运动，设点P运动的路程为x，的面积为y，下列图象能表示y与x之间函数关系的是（ ）
A． B． C． D．
10．如图，点O为正方形ABCD的中心，BE平分交DC于点E，延长BC到点F．
使，连接DF交BE的延长线于点H，连接OH交DC于点G，连接HC，则下列结论：①；②；③．
正确的个数有（ ）个
A．0 B．1 C．2 D．3
二、填空题（共8个小题，每小题3分，共24分，请将答案填在答题卷的答案栏内）
11．如图，点P在坐标平面内位置如图所示，则点P的坐标为________．
12．如图，□ABCD中，，请添加一个条件________，可得出该四边形是正方形．
13．如图，在中，，AD是的平分线，，，则的面积是________．
14．若直线向上平移4个单位长度后经过点（4，m），则m的值为________．
15．如图，在平面直角坐标系中，已知正比例函数与一次函数的图象如图所示，则关于x的一元一次不等式组的解集是________．
16．如图，菱形ABCD的周长为16，，E为AD的中点，M为AC上任意一点，则的最小值为________．
17．快车与慢车分别从广州、永州两地同时相向出发，匀速而行，快车到达永州后停留1h，然后按原路原速返回，快车比慢车晚1h到达广州，快慢两车距各自出发地的路程y（km）与所用的时x（h）的关系如图所示．下列说法：
①广州、永州两地之间的路程为480km； ②慢车的速度是60km/h；
③出发6h，快慢两车第一次相遇。
其中正确的有________．（填序号）。
18．如图，四边形是边长为2的正方形，点、分别在x，y轴负半轴上，连接，以的长为边长作正方形，点在y轴负半轴上，点在x轴的正半轴上；连接，以的长为边长作正方形，点、分别在x，y轴的正半轴上，依次规律作下去，点的坐标为________．
三、解答题（本大题共8个小题，共66分，解答题要求写出证明步骤或解答过程）
19．（本小题6分）如图，在平面直角坐标系中，已知的三个顶点坐标分别是A（，4），B（，2），C（，3）．
（1）将向下平移5个单位长度得到，请画出；
（2）画出关于y轴对称的，并写出的坐标；
（3）求的面积．
20．（本小题6分）已知点P（3，）在一次函数（b为常数）的图象上．
（1）求b的值；
（2）若点Q（m，）在这个一次函数的图象上，求m的值．
21．（本小题6分）如图，点C在线段BE上，点A、D在BE的同侧，，，且，，求证：．
22．（本小题8分）将永州潇湘大道某雷达测速区监测到的一组汽车的时速数据整理，得到其频数及频率如下表（不完整），其中30～40为时速大于等于30千米而小于40千米，其他类同．
（1）请把表中的数据填写完整，并补全频数分布直方图；
（2）若该雷达测速要求时速大于等于60千米即为违章，则违章车辆共有多少辆？
23．（本小题8分）如图，矩形ABCD的对角线相交于点O，，
（1）求证：四边形OCED是菱形；
（2）若，菱形OCED面积是20，求AC的长．
24．（本小题10分）在海平面上有A，B，C三个标记点，C为灯塔．港口A在灯塔C的北偏西方向上，港口A与灯塔C的距离是40海里；港口B在灯塔C的南偏西方向上，港口B与灯塔C的距离是30海里，一艘货船将从A港口沿直线向港口B运输货物，货船的航行速度为20海里/小时．
（1）货船从A港口航行到B港口需要多少时间；
（2）为了保障航行的安全，C处灯塔将向航船发送安全信号，信号有效覆盖半径为25海里，这艘货船在由A港口向B港口运输货物过程中，为保证安全航行，货船接收灯塔的安全信号时间不低于0.6小时才符合航行安全标准。问：这艘货船在本次运输中是否符合航行安全标准，并说明理由？
25．（本小题10分）2024年4月25日，神舟十八号载人飞船发射取得圆满成功．某航天模型销售店看准商机，推出“神舟”和“天宫”模型．已知销售店老板购进1个“神舟”模型和2个“天宫”模型一共需要100元；购进2个“神舟”模型和3个“天宫”模型一共需要170元．
（1）求每个“神舟”模型和“天宫”模型的进货价格；
（2）该航天模型销售店计划购进两种模型共100个，且“神舟”模型的数量不超过“天宫”模型数量的一半．若每个“神舟”模型的售价为50元，每个“天宫”模型的售价为35元，则购进多少个“神舟”模型时，销售这批模型的利润最大？最大利润是多少元？
26．（本小题12分）如图，取一张矩形的纸片进行折叠，具体操作过程如下：
（1）【课本再现】
第一步：如图1，对折矩形纸片ABCD，使AD与BC重合，折痕为EF，把纸片展平；
第二步：在AD上选一点P，沿BP折叠纸片，使点A落在矩形内部的点M处，连接PM，BM，根据以上操作，当点M在EF上时，________°；
（2）【类比应用】
如图2，现将矩形纸片换成正方形纸片，继续探究，过程如下：将正方形纸片ABCD按照（1）中的方式操作，并延长PM交CD于点Q，连接BQ，当点M在EF上时，求的度数；
（3）【拓展延伸】
在（2）的探究中，正方形纸片的边长为4cm，改变点P在AD上的位置（点P不与点A，D重合），沿BP折叠纸片，使点A落在矩形内部的点M处，连接PM，BM，并延长PM交CD于点Q，连接BQ．当时，请求出AP的长。
2024年上期义务教育质量监测
八年级数学参考答案及评分标准
一、选择题（本大题共10小题，每小题3分，共30分）
二、填空题（本大题共8小题，每小题3分，共24分）
11．（5，） 12．（或答案不唯一） 13．6
14．0 15． 16．
17．①② 18．（，）．
三、解答题（本大题共8小题，共66分）
19．（本小题满分6分）
（1）解：如图所示，即为所求；
（2）解：如图所示，即为所求；（4，2）
（3）解：
20．（本小题满分6分）
（1）解：把点P（，3）的坐标代入一次函数得：
，
解得：；
（2）解：由（1）得：一次函数的关系式为
把Q（m，）代入得：，
解得：．
21．（本小题满分6分）
证明：∵，，，
∴，
∴．
∵，
∴，
∴，
∴，
∴．
22．（本小题满分8分）
（1）解：汽车总数是：（辆），
40～50的频率是：，
50～60的频数是：（辆），
60～70的频数是：（辆），
60～70的频率是：；
频率合计：1
表中的数据填写完整如下：
补全频数分布直方图如下：
；
（2）解：∵时速不低于60千米即为违章，
∴（辆），
答：违章车辆共有76辆．
23．（本小题满分8分）
（1）证明：∵，，
∴四边形OCED是平行四边形，
∵四边形ABCD是矩形，
∴，，，
∴，
∴□OCED是菱形
（2）解法一：∵，
∴，
连接OE，交CD于F，则，
设，则，
∵，，
∴，
∴
，
∵，
，
∴．
解法二：（略）
24．（本小题满分10分）
（1）解：由已知得：，
（海里），
（小时），
答：货船从A港口到B港口需要2.5小时；
（2）答：这艘船在本次运输中符合航行安全标准，理由如下：
如图：过C作交AB于D，
在AB上取两点M，N使得（海里）
∵，
∴（海里），
∴（海里），
∵且，
∴（海里），
∴（小时）
∵，
∴这艘货船在本次运输中符合航行安全标准．
25．（本小题满分10分）
解：（1）设每个“神舟”模型的进货价格为x元，每个“天宫”模型的进货价格为y元．
由题意得，
解得．
答：每个“神舟”模型的进货价格为40元，每个“天宫”模型的进货价格为30元．
（2）设购进m个“神舟”模型，个“天宫”模型时，销售这批模型的利润最大，最大利润为w元．
由题意得，．
由，
解得，，
∵，
∴w随m的增大而增大．由题意知，m取整数．
∴当时，w取得最大值，为（元）．
∴当购进33个“神舟”模型时，销售这批模型的利润最大，最大利润为665元．
26．（本小题满分12分）
解：（1）30
（2）解：如图，
同（1）可证，
∴，
在正方形ABCD中，，，
由折叠知，，
∴，，
在和中，
，
∴，
∴，
∴，
（3）解：当点Q在点F的下方时，如图，
∵正方形ABCD中，，
∴，
∴，
由（2）知，
∴，
设，由折叠知，
∴，，
在中，，
∴，
解得，即；
当点Q在点F的上方时，如图，
则，
∴，
∴，
设，
则，，
在中，，
∴，
解得，即；
综上可知，AP的长为或．数据段
频数
频率
30～40
10
0.05
40～50
36
________
50～60
________
0.39
60～70
________
________
70～80
20
0.10
合计
________
________
题号
1
2
3
4
5
6
7
8
9
10
答案
B
A
A
D
B
D
D
B
B
D
数据段
频数
频率
30～40
10
0.05
40～50
36
0.18
50～60
78
0.39
60～70
56
0.28
70～80
20
0.10
总计
200
1