初中数学苏科版八年级上册1.3 探索三角形全等的条件课后复习题

这是一份初中数学苏科版八年级上册1.3 探索三角形全等的条件课后复习题，文件包含13探索三角形全等的条件第1课时分层练习原卷版docx、13探索三角形全等的条件第1课时分层练习解析版docx等2份试卷配套教学资源，其中试卷共11页， 欢迎下载使用。

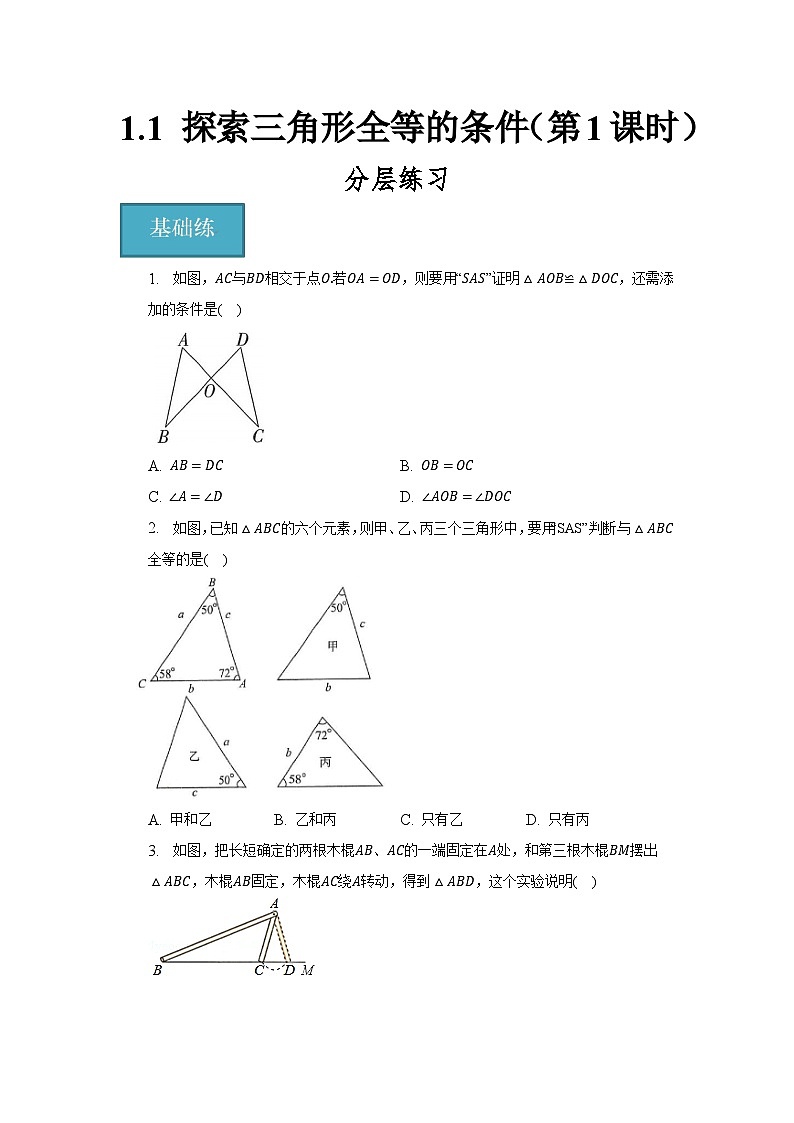
1. 如图，AC与BD相交于点O.若OA=OD，则要用“SAS”证明△AOB≌△DOC，还需添加的条件是( )
A. AB=DCB. OB=OC
C. ∠A=∠DD. ∠AOB=∠DOC
【答案】B
【解析】在△ABO和△DCO中，OA=OD,∠AOB=∠DOC,OB=OC,
所以△ABO≌△DCO(SAS)，故选B．
2. 如图，已知△ABC的六个元素，则甲、乙、丙三个三角形中，要用“SAS”判断与△ABC全等的是( )
A. 甲和乙B. 乙和丙C. 只有乙D. 只有丙
【答案】C
【解析】解：在△ABC和图乙的三角形中，满足三角形全等的判定方法：SAS，
所以乙和△ABC全等；
故选：C．
3. 如图，把长短确定的两根木棍AB、AC的一端固定在A处，和第三根木棍BM摆出△ABC，木棍AB固定，木棍AC绕A转动，得到△ABD，这个实验说明( )
A. △ABC与△ABD不全等
B. 有两边分别相等的两个三角形不一定全等
C. 两边和它们的夹角分别相等的两个三角形全等
D. 有两边和其中一边的对角分别相等的两个三角形不一定全等
【答案】D
【解析】解：由题意可知：AB=AB，AC=AD，∠ABC=∠ABD，
满足有两边和其中一边的对角分别相等，但是△ABC与△ABD不全等，
故选D．
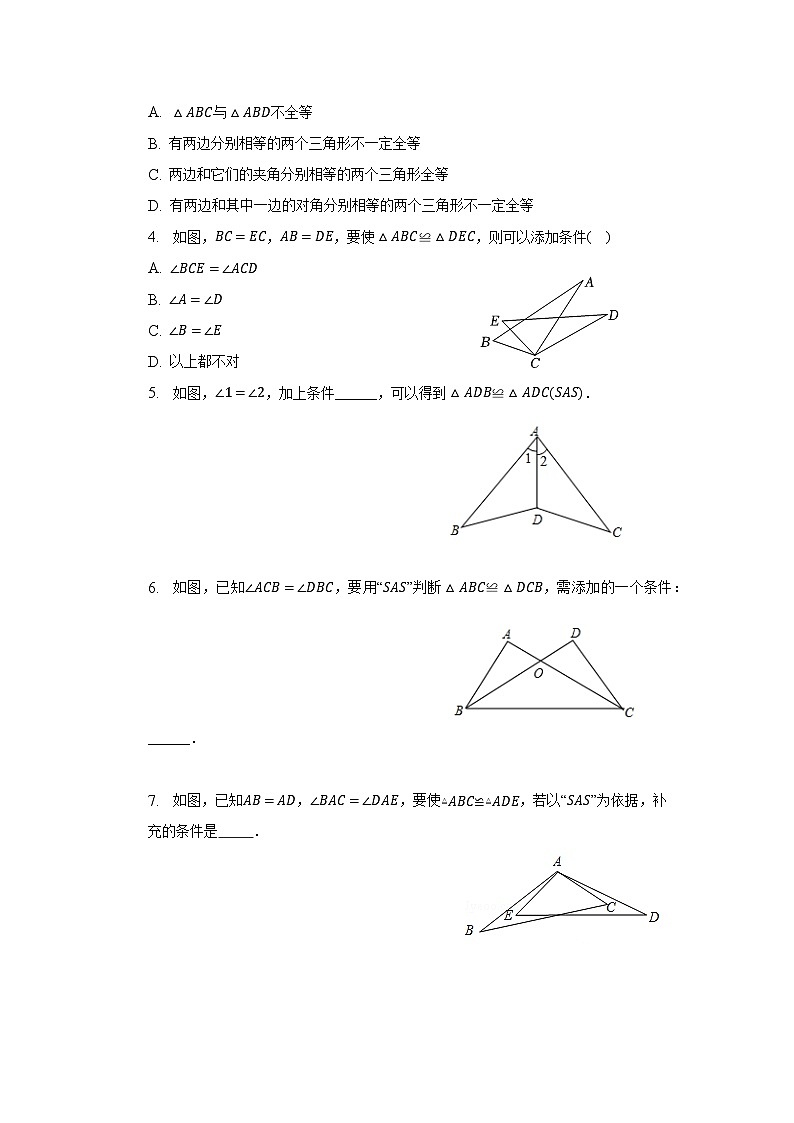
4. 如图，BC=EC，AB=DE，要使△ABC≌△DEC，则可以添加条件( )
A. ∠BCE=∠ACD
B. ∠A=∠D
C. ∠B=∠E
D. 以上都不对
【答案】C
【解析】解：A、由∠BCE=∠ACD，可以得到∠BCA=∠ECD，但不一定能判定△ABC≌△DEC；
B、添加∠A=∠D，不一定能判定△ABC≌△DEC；
C、因为BC=EC，AB=DE，添加条件∠B=∠E，由SAS，能判定△ABC≌△DEC；
故选：C．
5. 如图，∠1=∠2，加上条件______，可以得到△ADB≌△ADC(SAS)．
【答案】AB=AC
【解析】解：加上条件，AB=AC，可以得到△ADB≌△ADC(SAS)．
在△ADB与△ADC中，
AB=AC∠1=∠2AD=AD，
∴△ADB≌△ADC(SAS)，
故答案是：AB=AC．
6. 如图，已知∠ACB=∠DBC，要用“SAS”判断△ABC≌△DCB，需添加的一个条件：______．
【答案】AC=BD
【解析】解：添加的条件是：AC=BD，
理由是：∵在△ABC和△DCB中
AC=BD∠ACB=∠DBCCB=BC，
∴△ABC≌△DCB(SAS)，
故答案为：AC=BD．
7. 如图，已知AB=AD，∠BAC=∠DAE，要使▵ABC≌▵ADE，若以“SAS”为依据，补充的条件是 ．
【答案】AC=AE
【解析】
解：补充的条件是：AC=AE.理由如下：
∵在△ABC与△ADE中，AB=AD∠BAC=∠DAEAC=AE,
∴△ABC≌△ADE(SAS)．
故答案是：AC=AE．
8. 如图，在四边形ABCD中，由AB//CD，得∠ =∠ .若AB=CD，结合 = ，则△ABD≌△CDB(SAS)．
【答案】ABD CDB BD DB
【解析】见答案
9. 如图，有一池塘，要测池塘两端A、B之间的距离，可先在平地上取一点C，从点C不经过池塘可以直接到达点A和B，连接AC并延长到点D，使CD=CA，连接BC并延长到点E，使CE=CB，连接DE，那么量出DE的长就是A、B之间的距离，为什么?请结合解题过程，完成本题的证明．
证明：在△DEC和△ABC中，
CD= ， ，CE= ，_____________，
所以△DEC≌△ABC(SAS)，
所以 ．
【答案】CA ∠DCE=∠ACB CB DE=AB
【解析】在△DEC和△ABC中，
CD=CA,∠DCE=∠ACB,CE=CB,
所以△DEC≌△ABC(SAS)
所以DE=AB．
10. 如图，点D在AB上，点E在AC上，AB=AC，BD=CE，求证：∠B=∠C．
【答案】证明：∵AB=AC，BD=CE，
∴AB−BD=AC−CE，即AD=AE，
在△ACD和△ABE中，
∵AD=AE∠A=∠AAC=AB
∴△ACD≌△ABE(SAS)．
∴∠B=∠C.
1. 如图，已知点A，D，C，F在同一条直线上，AB=DE，BC=EF，要使△ABC≌△DEF，还需要添加一个条件是( )
A. ∠B=∠EB. ∠BCA=∠FC. BC//EFD. ∠A=∠EDF
【答案】A
【解析】解：A、∵AB=DE，BC=EF，∠B=∠E，
∴△ABC≌△DEF(SAS)，
故A符合题意；
B、∵AB=DE，BC=EF，∠BCA=∠F，
∴不能使△ABC≌△DEF，
故B不符合题意；
C∵BC//EF，
∴∠BCA=∠F，
∵AB=DE，BC=EF，∠BCA=∠F，
∴不能使△ABC≌△DEF，
故C不符合题意；
D、∵AB=DE，BC=EF，∠A=∠EDF，
∴不能使△ABC≌△DEF，
故D不符合题意；
故选：A．
2. 在测量一个小口圆形容器的壁厚(厚度均匀)时，小明用“X型转动钳”按如图方法进行测量，其中OA=OD，OB=OC，测得AB=3厘米，EF=4厘米，圆形容器的壁厚是( )
A. 2厘米
B. 1.5厘米
C. 1厘米
D. 0.5厘米
【答案】D
【解析】解：在△AOB和△DOC中，
OA=OD∠AOB=∠DOCOB=OC，
所以△AOB≌△DOC(SAS)，
所以AB=CD=3厘米，
因为EF=4厘米，
所以圆柱形容器的壁厚是12×(4−3)=0.5(厘米)，
故选：D．
如图，已知AB//CD，AB=CD，BE=CF．
求证：(1)△ABF≌△DCE；
(2)AF//DE．
【答案】证明：(1)∵AB//CD，
∴∠B=∠C，
∵BE=CF，
∴BE−EF=CF−EF，
即BF=CE，
在△ABF和△DCE中，
∵AB=CD∠B=∠CBF=CE，
∴△ABF≌△DCE(SAS)；
(2)∵△ABF≌△DCE，
∴∠AFB=∠DEC，
∴∠AFE=∠DEF，
∴AF//DE．