




数学八年级上册1.3 探索三角形全等的条件课堂教学ppt课件
展开1.探索并掌握两个三角形全等的条件“SSS”;
3.了解三角形的稳定性和及其在生活中的应用.
2.能利用“SSS”判定两个三角形全等,并能解决一些简单的实际问题,初步了解添加辅助线构造全等三角形;
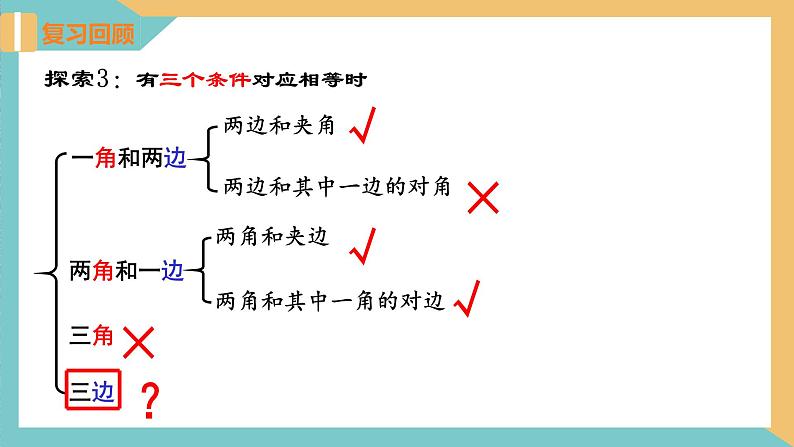
探索3:有三个条件对应相等时
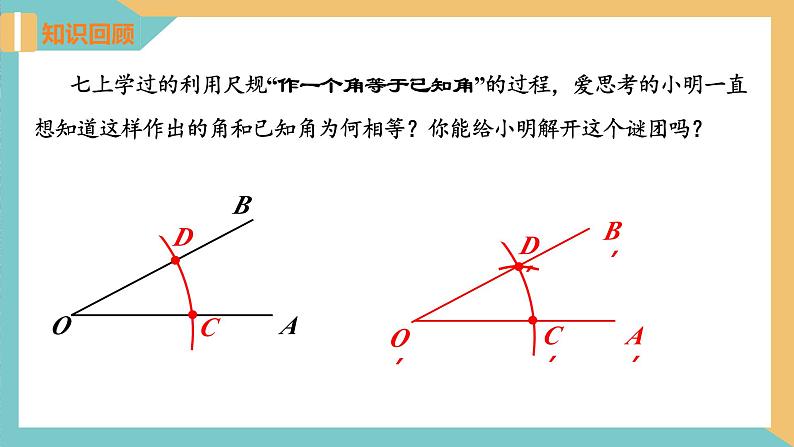
七上学过的利用尺规“作一个角等于已知角”的过程,爱思考的小明一直想知道这样作出的角和已知角为何相等?你能给小明解开这个谜团吗?
操作1:每人用事先准备好的一根长20cm的铁丝围成一个三角形,要求小组内的同学围成的三角形全等,小组讨论制作方法,全班交流.
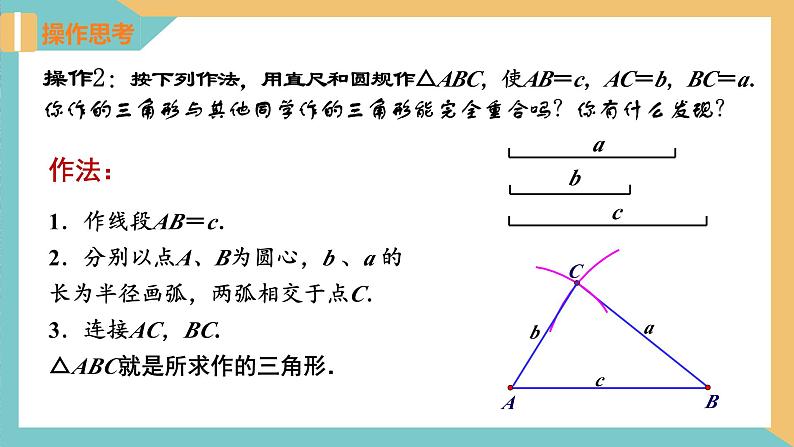
操作2:按下列作法,用直尺和圆规作△ABC,使AB=c,AC=b,BC=a.
1你作的三角形与其他同学作的三角形能完全重合吗?你有什么发现?
作法:1.作线段AB=c.2.分别以点A、B为圆心,b 、a 的长为半径画弧,两弧相交于点C.3.连接AC,BC.△ABC就是所求作的三角形.
(1)用准备好的硬纸条(数学实验手册附录1),分别钉成三角形、四边形、五边形,分别拉动三角形、四边形、五边形的两条边,它们的形状发生变化吗?
从上述操作中,你能得出判定两个三角形全等的新方法吗?概括你的发现.
(2)想办法固定四边形、五边形的形状,说说你的理由.
以上实践告诉我们判定两个三角形全等的一个基本事实:
三边分别相等的两个三角形全等.(简写成“边边边”或“SSS”)
下列图形中,哪两个三角形全等?
你能给小明解开这个谜团了吗?
如果一个三角形三边的长度确定,那么这个三角形的形状和大小就完全确定.三角形的这个性质叫做三角形的稳定性.
这个事实也说明了“三边分别相等的两个三角形全等”.
三角形的稳定性在生活和生产中有着广泛的应用.
当一个四边形四边的长度确定时,这个四边形的形状和大小不唯一确定.
四边形的不稳定性在生活中也有着广泛的应用.
例1.如图,C点是线段BF的中点,AB=DF, AC=DC.△ABC和△DFC全等吗?
变式1 若将上题中右边的三角形向左平移(如图),若AB=DF,AC=DE,BE=CF.问:△ABC和△DFE全等吗?
变式2 若将上题中的三角形继续向左平移(如图),若AB=DC,AC=DB,问:△ABC≌△DCB 吗?
变式3 若将上题中的三角形拉开,再翻折形成下图(如图),若AB=DF, BE=CF, AC=DE, 那么∠A与∠D相等吗? 为什么?
例2.已知:如图,在△ABC 中,AB=AC. 求证:∠B=∠C.
∴ △ABD ≌△ ACD(SSS).
证明:作△ABC 的中线AD.
∴ ∠B=∠C (全等三角形的对应角相等).
还有不同方法证明∠B=∠C?
为什么需要作辅助线,它的意图是什么?
作辅助线,为了把∠B、∠C放在的三角形中.
∴ △ABD ≌△ ACD(SAS).
方法2:作△ABC 的角平分线AD.
作△ABC 的高线AD,能证明∠B=∠C吗?
1.在四边形ABCD中,AB=AD,CB=CD.请你添加一条线段把它分成两个全等三角形,并给出证明.
2.已知,AB=DC,DB=AC.
求证:∠ABD=∠DCA.
3.如图,方格纸中的△DEF的3个顶点分别在小正方形的顶点(格点)上,像这样三个顶点都在格点上的三角形叫格点三角形,请在图中再画1个格点三角形与△DEF全等.这样的格点三角形你能画几个?
初步了解添加辅助线构造全等三角形
1.肖老师为班级中每名同学准备了长分别为a、b、c三根木条,所有同学都用三根木条,首尾顺次拼接组成三角形,这时小陈同学说:“我们所有人的三角形,形状和大小是完全一样的”小陈同学的说法依据_______.
2.在建筑工地上我们常可以看见如图所示的用木条EF固定长方形门框ABCD的情形.这种做法的依据是________________.
3.如图,在△ABC中,AB=AC,EB=EC,则由“SSS”可以判定( )A.△ABD≌△ACD B.△ABE≌△ACEC.△BDE≌△CDE D.以上答案都不对
4.如图,在△ACE和△BDF中,AE=BF,CE=DF,要利用“SSS”证△ACE≌△BDF时,需添加一个条件是( )
A.AB=BC B.DC=BC C.AB=CD D.以上都不对
5.如图,AB=CD,AD=BC, 则下列结论: ①△ABC≌△CDB;②△ABC≌△CDA;③△ABD ≌△CDB;④BA∥DC. 正确的个数是 ( )A . 1个 B. 2个 C. 3个 D. 4个
6. 如图1,油纸伞是中国传统工艺品之一,起源于中国的一种纸制或布制伞.油纸伞的制作工艺十分巧妙,如图2,伞圈D沿着伞柄AP滑动时,总有伞骨BD=CD,AB=AC,从而使得伞柄AP始终平分同一平面内两条伞骨所成的∠BAC.请你说明其中的理由.
7.已知:如图 ,AB=AE,AC=AD,BD=CE,求证:△ABC≌△AED.
∴BD-CD=CE-CD .
在△ABC和△ADE中,
AC=AD(已知),AB=AE(已知),BC=ED(已证),
∴△ABC≌△AED(SSS).
8.已知:如图,AB=CD,AD=CB, 求证:①∠A=∠C;
② AB∥DC,AD∥ BC
②证明:∵ △ABD≌△CDB(已证) ,∴∠ABD=∠CDB, ∠ADB=∠CBD .(全等三角形的对应角相等)∴AB∥DC,AD∥BC. (内错角相等,两直线平行)
苏科版八年级上册1.3 探索三角形全等的条件备课课件ppt: 这是一份苏科版八年级上册<a href="/sx/tb_c17288_t3/?tag_id=26" target="_blank">1.3 探索三角形全等的条件备课课件ppt</a>,共32页。PPT课件主要包含了学习目标,注意点,两边一角对应相等,再次强调,边角边,△ACE,SAS等内容,欢迎下载使用。
苏科版八年级上册1.3 探索三角形全等的条件教案配套ppt课件: 这是一份苏科版八年级上册<a href="/sx/tb_c17288_t3/?tag_id=26" target="_blank">1.3 探索三角形全等的条件教案配套ppt课件</a>,共28页。PPT课件主要包含了学习目标,AO=BO,AAS,CO=DO,ACBD,ASA,∠AOC∠BOD,𝑪𝑶𝑫𝑶,ABDC,SAS等内容,欢迎下载使用。
苏科版八年级上册1.3 探索三角形全等的条件课文ppt课件: 这是一份苏科版八年级上册<a href="/sx/tb_c17288_t3/?tag_id=26" target="_blank">1.3 探索三角形全等的条件课文ppt课件</a>,共27页。PPT课件主要包含了学习目标,一角和两边,两边和夹角,两边和其中一边的对角,两角和一边,两角和夹边,两角和其中一角的对边,∴∠C=∠P,角边角的推论,一组等角的“对边”等内容,欢迎下载使用。













