初中数学苏科版八年级上册1.2 全等三角形教学课件ppt

这是一份初中数学苏科版八年级上册1.2 全等三角形教学课件ppt，共56页。PPT课件主要包含了学习目标，全等三角形，全等图形，一般三角形，直角三角形，SAS，ASA，AAS，SSS，尺规作图等内容，欢迎下载使用。
1. 熟练掌握判定两个三角形全等的条件，并会灵活运用它们解决实际问题 ；
2. 通过推理和证明，学会探究复杂问题的方法和技巧，不断积累学习经验，提升分析问题和解决问题的能力.
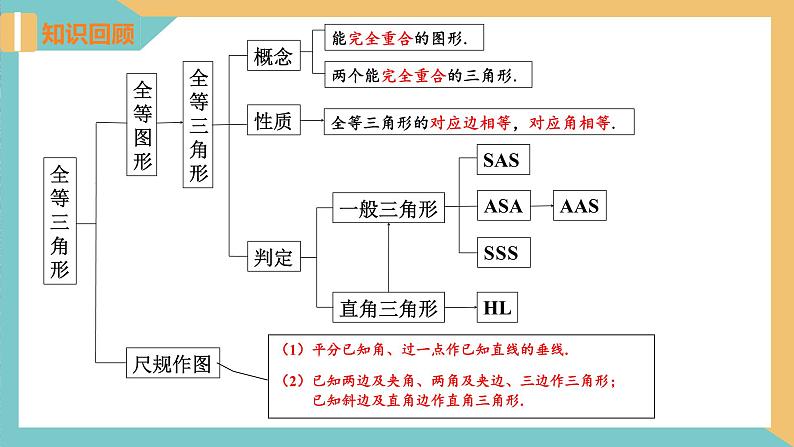
两个能完全重合的三角形.
全等三角形的对应边相等，对应角相等.
（1）平分已知角、过一点作已知直线的垂线.
（2）已知两边及夹角、两角及夹边、三边作三角形； 已知斜边及直角边作直角三角形.
考点一 全等图形识别
例（2021秋·河北保定·八年级校考阶段练习）下列图形：①两个正方形；②每边长都是 的两个四边形；③每边都是 的两个三角形；④半径都是 的两个圆．其中是一对全等图形的是（ ）A．1个 B．2个 C．3个 D．4个
提示：根据能够完全重合的两个图形叫做全等形，结合各项说法作出判断即可．
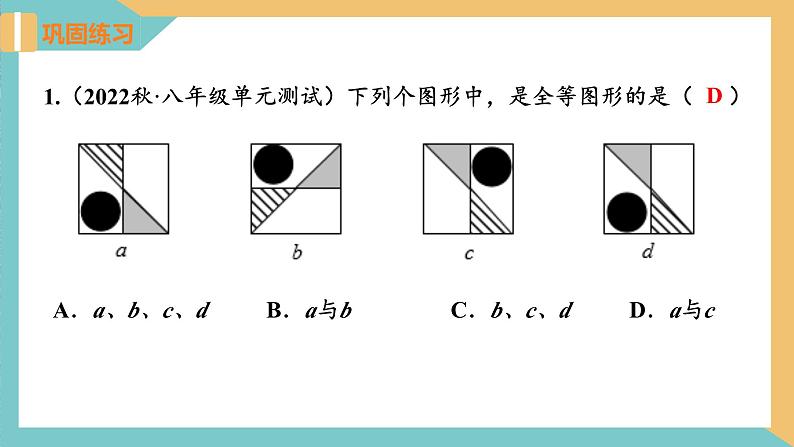
1.（2022秋·八年级单元测试）下列个图形中，是全等图形的是（ ）
A．a、b、c、d B．a与b C．b、c、d D．a与c
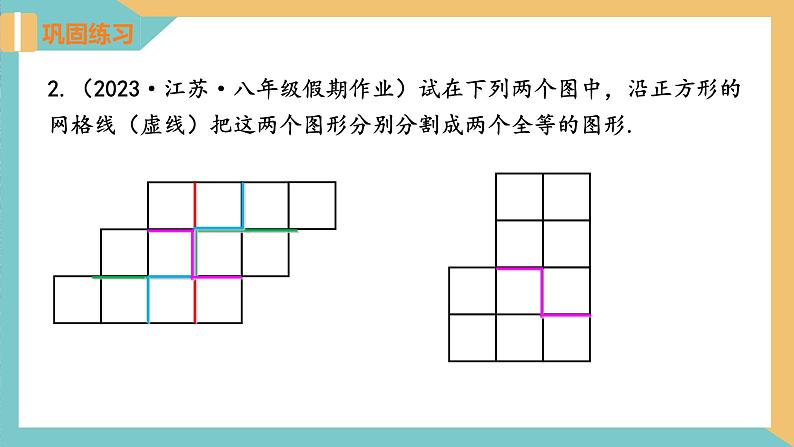
2.（2023·江苏·八年级假期作业）试在下列两个图中，沿正方形的网格线（虚线）把这两个图形分别分割成两个全等的图形.
考点二 全等三角形的概念
例1（2023·浙江·八年级假期作业）下列说法正确的是（ ）A．全等三角形是指形状相同的两个三角形 B．全等三角形是指面积相等的两个三角形C．全等三角形的周长和面积分别相等D．所有的等边三角形是全等三角形
提示：根据全等三角形的概念即可得到答案．
1.（2023·全国·八年级假期作业）已知△ABC≌△DEF，且∠A与∠D是对应角，∠B和∠E是对应角，则下列说法中正确的是（ ）A．AC与DF是对应边 B．AC与DE是对应边C．AC与EF是对应边 D．不能确定AC 的对应边
AB与BA，BC与AD
考点三 全等三角形的性质
1.（2021·黑龙江哈尔滨·统考中考真题）如图，△ABC≌△DEC，点A和点D是对应顶点，点B和点E是对应顶点，过点A作AF⊥CD ，垂足为点F，若∠BCE=65°，则∠CAF的度数为（ ）A．30° B．25° C．35° D．65°
解：∵△ABC≌△DEC，∴∠ACB=∠DCE，∴∠ACB-∠ACE=∠DCE-∠ACE，即∠ACF=∠BCE，∵∠BCE=65°，∴∠ACF=∠BCE=65°，∵ AF⊥CD ，∴∠AFC=90°，∴∠CAF=90°-∠ACF=25°.
2.（2022秋·山东泰安·九年级校考期末）如图，正方形的网格中，∠1+∠2+∠3十∠4+∠5等于（　　）A．175° B．180° C．210° D．225°
解：∵∠1和∠5所在的三角形全等，∴∠1+∠5＝90°，∵∠2和∠4所在的三角形全等，∴∠2+∠4＝90°，而：∠3＝45°，∴∠1+∠2+∠3十∠4+∠5＝225°．
提示：此题需要分类讨论．
全等三角形性质的“两点应用”:(1)求线段:全等三角形的对应边相等,可以利用这一性质直接确定对应边的数量关系,也可以间接求解相关线段的长度等问题;(2)求角:全等三角形的对应角相等,可以利用这一性质直接确定对应角的数量关系,也可以间接求解相关角的度数等问题.
考点四 全等三角形的判定
例1（2019·南京期末）在△ABC和△DEF中①∠A=∠E、AB=EF、∠C=∠D；②∠A=∠D、AB=EF、∠B=∠E；③∠A=∠F、AB=DF、∠B=∠D；④∠A=∠F、AB=EF、CB=ED；⑤∠A=∠D、∠B=∠E、BC=EF.其中能判定这两个三角形全等的条件有（ ）A.①②④ B.①③⑤ C.④⑤ D.①③
1.（2022秋·八年级课时练习）如图，已知∠1＝∠2，AB＝AD，请添加一个条件，使△ABC≌△ADE，并加以证明．(1)你添加的条件是__________________（只需添加一个条件）；
解:(1)添加的条件可以为：∠ACB=∠AED或AE=AC或∠D=∠B（任选一个即可）．
2.（2023秋·八年级课时练习）如图，在△ABC中，D是BC的中点，DE⊥AB，DF⊥AC，垂足分别是E，F，BE=CF．(1)图中有几对全等的三角形？请一一列出．
解:（1）3对．分别是：△ABD≌△ACD；△ADE≌△ADF；△BDE≌△CDF．
(2)选择一对你认为全等的三角形进行证明．
考点五 全等三角形的判定和性质综合运用
例1（2018·兴化期末）如图，在四边形ABCD中，AD∥BC，E为CD的中点，连接AE、BE，BE⊥AE，延长AE交BC的延长线于点F.(1)求证：AD=FC；
(2)求证：AB=BC+AD；
(3)若∠ABC=50°，求∠F的度数.
1.（2018春·江苏·九年级校联考专题练习）已知：如图， AB=AE ，AC=AD，∠BAE=∠CAD ．求证：BC=ED．
2.（2023春·七年级课时练习）如图，A，B两点分别位于一个池塘的两端，小明和小颖想用绳子测量A，B两点间的距离，他们想出了这样一个办法：先在地上取一个可以直接到达点A和点B的点C，连接AC并延长到D，使CD＝CA；连接BC并延长到E，使CE＝CB；连接DE并测量出它的长度，DE 的长度就是A、B两点间的距离”（1）你能说明其中的道理吗？
（2）你还有别的不同的方法吗？（可以使用直角工具）请写出具体方法，并说明理由．
解：（2）方法：在地面上取一个可以直接到达点A和点B的点C，连接AC，BC，使∠ACB＝90°，然后在AC的延长线上确定点D，使CD＝AC，连接BD并测量BD的长度，BD的长度就是A、B两点之间的距离，    
全等模型一--手拉手模型
拓展探究：如图2，把Rt△ACD绕点C逆时针旋转，线段AE、BD交于点F，则AE与BD之间的关系是否仍然成立？请说明理由．
1.（2022秋·八年级课时练习）如图所示，在平行四边形ABCD中，分别以AB、AD为边作等边△ABE和等边△ADF，分别连接CE，CF和EF，则下列结论，一定成立的个数是（　　）①△CDF≌△EBC；②△CEF是等边三角形；③∠CDF＝∠EAF；④CE∥DFA．1 B．2 C．3 D．4
全等模型二--一线三等角模型
解：(2)直线m在绕点A旋转一周的过程中，BD、DE、CE存在3种不同的数量关系：DE=BD+CE，DE=BD-CE，DE=CE-BD．如图1时，DE=BD+CE，如图2时，DE=BD-CE，如图3时，DE=CE-BD，（证明同理）
(3)如果“条件中”的“BD⊥直线m，CE⊥直线m , AB⊥AC”改为“∠BDA=∠AEC=∠BAC”,其他条件不变，请问△BDA与△AEC还全等吗？请说明理由．
如图，点B、C、E在同一条直线上，∠B＝∠E＝60°,∠ACF＝60°,且AB＝CE. 求证：AC＝CF.
2. 已知CD是经过∠BCA的顶点C的一条直线，CA＝CB，E、F分别是直线CD上的两点，且∠BEC＝∠CFA＝∠α. (1) 若直线CD经过∠BCA的内部，且点E、F在射线CD上，请解决下面的问题：
① 如图①，若∠BCA＝90°，∠α＝90°，探索线段EF、BE、AF之间的数量关系，并证明你的结论；
② 如图②，若0°＜∠BCA＜180°，请添加一个关于∠α与∠BCA关系的条件：_________________________，使①中的结论仍然成立．
∠α＋∠BCA＝180°
(2) 如图③，若直线CD经过∠BCA的外部，∠α＝∠BCA，请写出线段EF、BE、AF之间的数量关系，并证明你的结论．
延长AD至点E，使DE=AD，再连接 ，可证△ACD≌△EBD，从而把AB、AC、2AD集中在△ABE中，利用三角形三边的关系即可判断中线AD的取值范围是 （直接写出范围即可）．这种解决问题的方法我们称为“倍长中线法”．
常用辅助线--倍长中线法
解：(1)由题意，AD=DE，BD=CD，∠ADC=∠EDB，∴△ACD≌△EBD，∴BE=AC=6，∴AB-AC