初中数学苏科版八年级上册第五章 平面直角坐标系5.2 平面直角坐标系复习ppt课件

这是一份初中数学苏科版八年级上册第五章 平面直角坐标系5.2 平面直角坐标系复习ppt课件，共40页。PPT课件主要包含了学习目标，物体位置的确定，平面直角坐标系，概念和表示方法，点的坐标，相关概念，各象限内点的坐标特征，坐标轴上点坐标的特征，轴对称，方向和距离等内容，欢迎下载使用。

2. 掌握在平面直角坐标系中确定点的坐标描出点的位置的方法；
1. 理解物体的位置变化可以通过确定物体位置的数量变化来说明；
3. 掌握简单的对称图形、图形的平移的坐标关系.
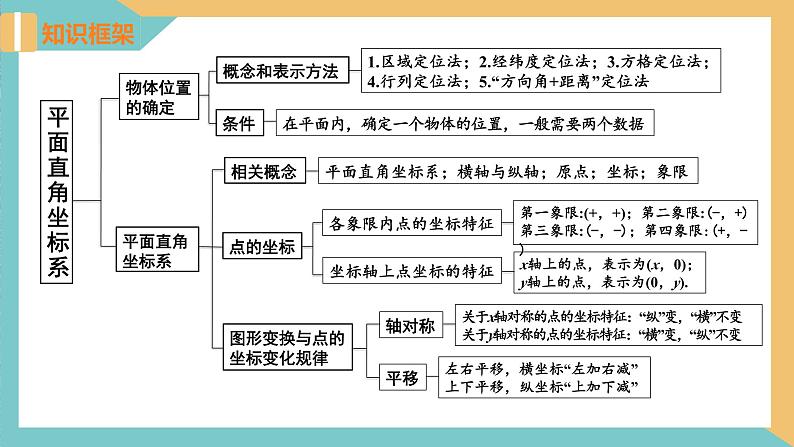
1.区域定位法；2.经纬度定位法；3.方格定位法；4.行列定位法；5.“方向角+距离”定位法
在平面内，确定一个物体的位置，一般需要两个数据
平面直角坐标系；横轴与纵轴；原点；坐标；象限
第一象限:(+，+)；第二象限:(-，+)第三象限:(-，-)；第四象限:(+，-)
x轴上的点，表示为(x，0)；y轴上的点，表示为(0，y).
图形变换与点的坐标变化规律
关于x轴对称的点的坐标特征：“纵”变，“横”不变关于y轴对称的点的坐标特征：“横”变，“纵”不变
左右平移，横坐标“左加右减”上下平移，纵坐标“上加下减”
考点一 位置的确定
例 如图是小军家与周围地区的行走路线示意图，相对小军家来说： ①小军家北偏东30°的方向上有 ； ②要想确定照相馆的位置，还需要 个数据； ③要确定小军家附近的学校的位置，需要 个数据，分别是 .
1.下列表述中，位置确定的是(　　)A.北偏东30° B.东经118°，北纬24°C.淮海路以北，中山路以南 D.银座电影院第2排
2.某班级第4组第5排位置可以用数对(4，5)表示，则数对(2，3)表示的位置是(　　)A.第3组第2排 B.第3组第1排 C.第2组第3排D.第2组第2排
3. 如图，点O、M、A、B、C在同一平面内.若规定点A的位置记为(50，20°)，点B的位置记为(30，60°)，则点C的位置应记为________________．
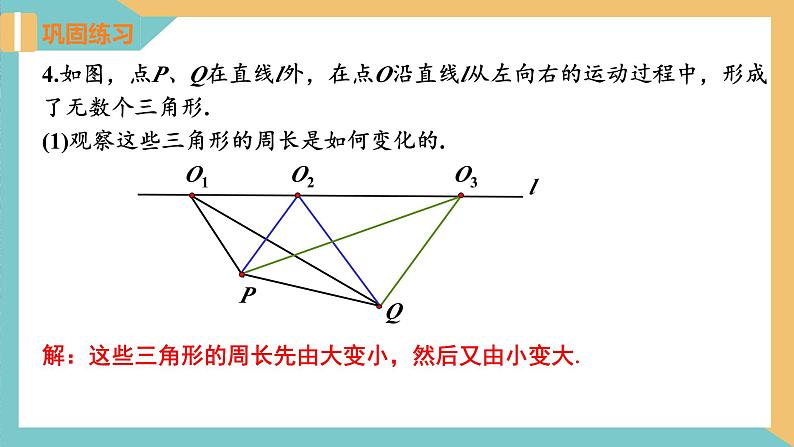
4.如图，点P、Q在直线l外，在点O沿直线l从左向右的运动过程中，形成了无数个三角形.(1)观察这些三角形的周长是如何变化的.
解：这些三角形的周长先由大变小，然后又由小变大.
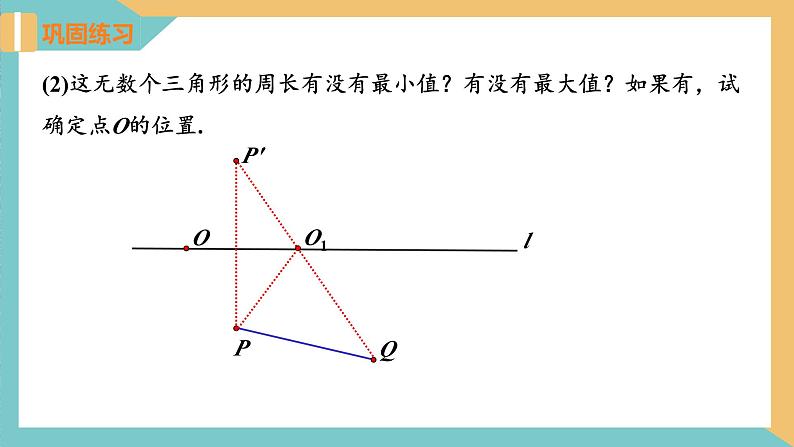
(2)这无数个三角形的周长有没有最小值？有没有最大值？如果有，试确定点O的位置.
例 在平面直角坐标系中，(1)已知点P（a﹣1，3a+6）在y轴上，求点P的坐标；
解：(1)∵点P（a﹣1，3a+6）在y轴上，∴a﹣1＝0，解得a＝1，∴3a+6＝3×1+6＝9，∴P（0，9）.
考点二 平面直角坐标系中点的坐标特征
解：(2)∵AB∥x轴，∴m＝4，∵点B在第一象限，∴n＞0，∴m＝4，n＞0.
(2)已知两点A（﹣3，m），B（n，4），若AB∥x轴，点B在第一象限，求m的值，并确定n的取值范围；
(3)在(1)(2)的条件下，如果线段AB的长度是5，求以P、A、B为顶点的三角形的面积S．
1.已知点M(1-2m，m-1)在第四象限，则m的取值范围是________.
2.点P（2a﹣1，a+2）在x轴上，则点P的坐标为__________．
解：由题意，得a+2＝0，解得a＝﹣2，2a﹣1＝﹣5，点P的坐标为（﹣5，0）.
3.若点A（6，6），AB∥x轴，且AB＝2，则B点坐标为( )A.（4，6） B.（6，4）或（6，8）C.（6，4） D.（4，6）或（8，6）
解：∵A（6，6），AB∥x轴，∴点B的纵坐标为6，点B在点A的左边时，6﹣2＝4，此时点B的坐标为（4，6），点B在点A的右边时，6+2＝8，此时，点B的坐标为（8，6），综上所述，点B的坐标为（4，6）或（8，6）．
5. 已知平面直角坐标系中有一点M（m﹣1，2m+3）（1）当m为何值时，点M到x轴的距离为1？（2）当m为何值时，点M到y轴的距离为2？
解：（1）∵|2m+3|＝12m+3＝1或2m+3＝﹣1∴m＝﹣1或m＝﹣2；
（2）∵|m﹣1|＝2m﹣1＝2或m﹣1＝﹣2∴m＝3或m＝﹣1．
(2)(1)中的△A'B'D的面积为____. 
考点三 关于坐标轴对称的点的坐标特征
例 在平面直角坐标系xOy中，已知A(-1，4)，B(4，2)，C(-1，0)三点.(1)点A关于y轴的对称点A′的坐标为　　　，点B关于x轴的对称点B′的坐标为_______，线段AC的垂直平分线与y轴的交点D的坐标为_______; 
1.在平面直角坐标系中，点P（a，-6）关于x轴对称点为Q（2，b），则a+b的值为( )A．﹣8 B．8 C． - 4 D．4
解：∵点P（a， -6）与点Q（2，b）关于x轴对称，∴a＝2，b＝6，∴a+b＝2+6＝8．
4.已知点A(2，0)，B(0，4)，点P在x轴上，且△PAB的面积为10，则点P的坐标为__________________.
(－3，0)或(7，0)
5.在平面直角坐标系xOy中，点A与点A1关于x轴对称，点A与点A2关于y轴对称.已知点A1(1，2)，则点A2的坐标是___________.
例 如图，△A′B′C′是△ABC经过平移得到的，△ABC三个顶点的坐标分别为A(-4，-1)，B(-5，-4)，C(-1，-3)，△ABC中任意一点P(x1，y1)平移后的对应点为P′(x1+6，y1+4).(1)请写出三角形ABC平移的过程；
考点四 点的平移与坐标变化规律
解：(1)∵△ABC中任意一点P(x1，y1)平移后的对应点为P′(x1+6，y1+4)，∴平移后对应点的横坐标加6，纵坐标加4，∴△ABC先向右平移6个单位，再向上平移4个单位得到△A′B′C′或△ABC先向上平移4个单位，再向右平移6个单位得到△A′B′C′；
(2)写出点A′，C′的坐标；(3)求△A′B′C′的面积．
解：(2)由(1)可知，A′(2，3)，C′(5，1)；
1.在平面直角坐标系中，将△ABC各点的纵坐标保持不变，横坐标都减去3，则所得图形与原图形的关系是将原图形( )A．向上平移3个单位长度B．向下平移3个单位长度C．向左平移3个单位长度D．向右平移3个单位长度
解：将△ABC各点的纵坐标保持不变，横坐标都减去3，所得图形与原图形相比向左平移了3个单位．
2. 如图，在平面直角坐标系xOy中，将四边形ABCD先向下平移，再向右平移得到四边形A1B1C1D1，已知A(-3，5)，B(-4，3)，A1(3，3)，则点B1的坐标为(　　)A.(1，2) B.(2，1) C.(1，4) D.(4，1)
3. 已知P(a＋1，b－2)，Q(4，3)两点．若点P到y轴的距离是3，且PQ∥x轴，求点P的坐标．
解：∵点P到y轴的距离是3，∴点P的横坐标为3或－3.又∵PQ∥x轴，∴点P的纵坐标为3，∴点P的坐标为(3，3)或(－3，3)．
例1 如图，在平面直角坐标系中，点A，B的坐标分别是(－2，0)，(4，0)，现同时将点A，B向上平移2个单位长度，再向右平移2个单位长度，分别得到A，B的对应点C，D.连接AC，BD，CD.
(1)点C的坐标为________，点D的坐标为______，四边形ABDC的面积为________.
考点五 建立适当的平面直角坐标系确定点的坐标
(2)在x轴上是否存在一点E，使得△DEC的面积是△DEB面积的2倍？若存在，请求出点E的坐标；若不存在，请说明理由.
①当表示政府广场的点的坐标为(0，0)，表示庐江汽车站的点的坐标为(﹣2，﹣3)时，表示周瑜文化园的点的坐标为(6，﹣4)；②当表示政府广场的点的坐标为(0，0)，表示庐江汽车站的点的坐标为(﹣4，﹣6)时，表示周瑜文化园的点的坐标为（12，﹣8)；③当表示政府广场的点的坐标为(1，1)，表示庐江汽车站的点的坐标为(﹣3，﹣5)时，表示周瑜文化园的点的坐标为(13，﹣7)；④当表示政府广场的点的坐标为(1.5，1.5)表示庐江汽车站的点的坐标为(﹣4.5，﹣7.5)时，表示周瑜文化园的点的坐标为(19.5，﹣10.5)．上述结论中，所有正确结论的序号是_______________.
例2 如图是庐城一些地点的分布示意图．在图中，分别以向右，向上为x轴，y轴的正方向建立平面直角坐标系，有如下四个结论：
1. 如图所示，在正方形网格中，点A的坐标为(-1，0)，点B的坐标为(0，-2)，则点C的坐标为(　　)A. (1，1)B. (-1 ，-1)C. (-1，1)D. (1，-1)
解： ∵点A的坐标为(-1，0)，点B的坐标为(0，-2)，∴建立平面直角坐标系如图所示.∴点C的坐标为(1，1).
2.如图是轰炸机机群的一个飞行队形，如果最后两架轰炸机的坐标分别为A(-2，1)和B(-2，-3)，那么第一架轰炸机C的坐标是( )A. (-2，3) B. (2，-1) C．(-2，-1) D．(-3，2)
4.如图，菱形ABCD的边长为6，∠ABC=45°．(1)试建立适当的平面直角坐标系表示该菱形并写出其各顶点的坐标．
解：以点为坐标原点，菱形BC的所在的直线为x轴，BC所在直线的垂线为y轴建立平面直角坐标系，如图，
(2)若要计算该菱形的面积，你有什么办法？
例 如图，在平面直角坐标系xOy中，横坐标和纵坐标都为整数的点称为整点，观察图中每个正方形（实线）四条边上的整点的个数，假如按如图规律继续画正方形（实线），请你猜测由里向外第2023个正方形（实线）的四条边上的整点共有________个．
解：第1个正方形有4×1=4个整数点；第2个正方形有4×2=8个整数点；第3个正方形有4×3=12个整数点；…第n个正方形有4n个整数点；所以第2023个正方形有4×2023=8092个整数点．
考点六 点的坐标变化规律探索问题
1. 如图，在平面直角坐标系中，一动点从原点O出发，按向上，向右，向下，向右的方向不断地移动 , 每移动一个单位 , 得到点A1(0，1)，A2(1，1)，A3(1，0)，A4(2，0)，……，那么点A2023的坐标为_______________．