初中数学苏科版八年级上册第六章 一次函数6.3 一次函数的图像同步测试题

这是一份初中数学苏科版八年级上册第六章 一次函数6.3 一次函数的图像同步测试题，文件包含63一次函数的图像1分层练习解析版docx、63一次函数的图像1分层练习docx等2份试卷配套教学资源，其中试卷共13页， 欢迎下载使用。

考查题型一 描点法画一次函数图像
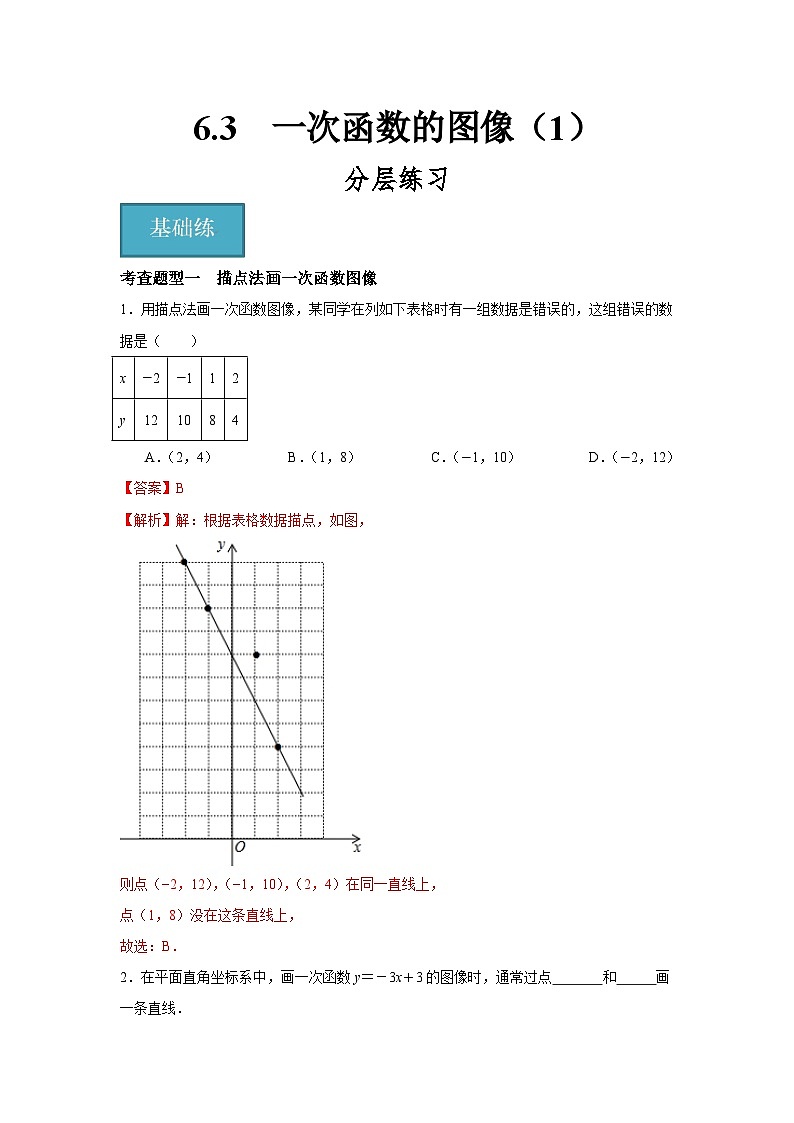
1．用描点法画一次函数图像，某同学在列如下表格时有一组数据是错误的，这组错误的数据是（ ）
A．（2，4） B．（1，8） C．（−1，10） D．（−2，12）
【答案】B
【解析】解：根据表格数据描点，如图，
则点（−2，12），（−1，10），（2，4）在同一直线上，
点（1，8）没在这条直线上，
故选：B．
2．在平面直角坐标系中，画一次函数y＝－3x＋3的图像时，通常过点 和 画一条直线．
【解析】解：根据题意，
∵画一次函数y＝－3x＋3的图像，
令x=0，则y=3，
令y=0，则x=1，
∴y=−3x+3与坐标轴的交点坐标为（0，3），（1，0）；
故答案为：（0，3），（1，0）；
3．把下面画函数y=2x−3的图像的过程补充完整，并根据图像直接写出函数与x轴、y轴的交点坐标．
解：列表为：
画出的函数图像为：
函数y=2x−3与x轴、y轴的交点坐标分别为__________、__________．
【解析】解：解：列表为：
画出的函数图像为：
对于函数y=2x-3，当x=0时，y=-3，当y=0时，由0=2x-3得x= 32
∴函数y=2x−3与x轴、y轴的交点坐标分别为（32，0）、（0，-3），
故答案为：-7，-5，-3，-1，1；（32，0）、（0，-3）．
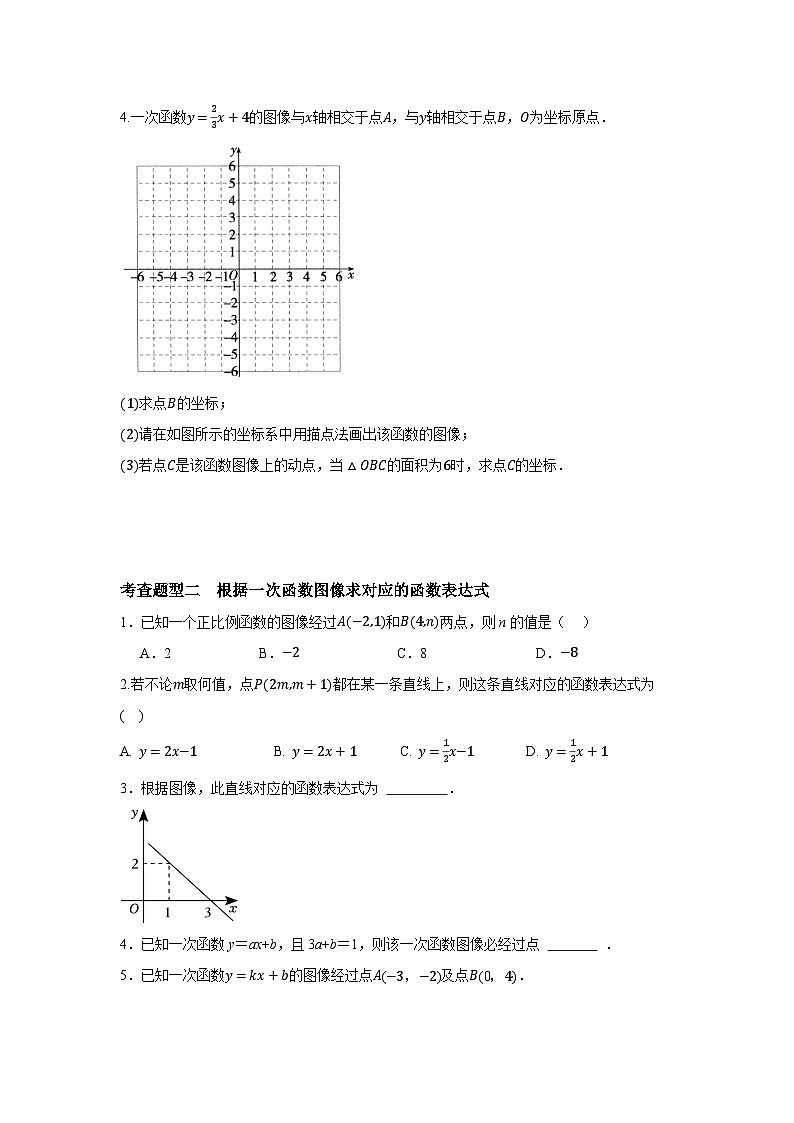
4.一次函数y=23x+4的图像与x轴相交于点A，与y轴相交于点B，O为坐标原点．
(1)求点B的坐标；
(2)请在如图所示的坐标系中用描点法画出该函数的图像；
(3)若点C是该函数图像上的动点，当△OBC的面积为6时，求点C的坐标．
【解析】(1)在y=23x+4中，当x＝0时，y＝4，
∴点B的坐标为(0，4)．
(2)在y=23x+4中，当y＝0时，x＝-6，
∴点A的坐标为(-6，0)．函数图像如图所示：
(3)设点C的坐标为x,23x+4，则点C到y轴的距离为|x|．
∵点B的坐标为(0，4)，
∴OB＝4．
∵△OBC的面积为6．
∴12OB⋅|x|=6，
即12×4|x|=6，解得x＝±3．
∴点C的坐标为(3，6)或(-3，2)．
考查题型二 根据一次函数图像求对应的函数表达式
1．已知一个正比例函数的图像经过A−2,1和B4,n两点，则n的值是（ ）
A．2B．−2C．8D．−8
【答案】B
【解析】解：设正比例函数表达式为y=kxk≠0，
将A−2,1，代入，得：k=−12，
∴y=−12x，
当x=4时，y=−12×4=−2，
∴n=−2；
故选B．
2.若不论m取何值，点P(2m,m+1)都在某一条直线上，则这条直线对应的函数表达式为
( )
A. y=2x−1B. y=2x+1C. y=12x−1D. y=12x+1
【答案】D
【解析】设x=2m，y=m+1，则m=12x.∴y=12x+1．
3．根据图像，此直线对应的函数表达式为 ．
【解析】解：设直线对应的函数表达式为y=kx+b，
把(1,2),(3,0)代入y=kx+b，得k+b=23k+b=0，
解得k=−1b=3，
∴直线达式为y=−x+3；
故答案为：y=−x+3．
4．已知一次函数y＝ax+b，且3a+b＝1，则该一次函数图像必经过点 ．
【解析】解：∵3a+b=1，
∴相当于y=ax+b中，当x=3时，y=1，
∴一次函数图像必过点(3,1)，
故答案为：(3,1)．
5．已知一次函数y=kx+b的图像经过点A(−3，−2)及点B(0，4)．
(1)求此一次函数的表达式，并画出图像；
(2)求此函数图像与两坐标轴所围成的三角形的面积．
【解析】（1）将点A(−3，−2)及点B(0，4)分别代入y=kx+b得：
−3k+b=−2b=4，
解得：k=2b=4，
∴该一次函数表达式为y=2x+4．
函数图像如图所示：
（2）由函数图像可知，此函数图像与两坐标轴所围成的三角形的面积即为△OBC的面积，
令0=2x+4，解得：x=−2，即：点C的坐标为−2,0，
∴OB=4，OC=2，
∴S△OBC=12OB·OC=12×4×2=4，
∴此函数图像与两坐标轴所围成的三角形的面积为4．
已知y－2与x+2成正比例，且x=1时，y=8.
⑴求y与x之间的函数表达式；
⑵ 在平面直角坐标系中，① 画出 ⑴ 中的y与x之间的函数表达式的图像；
②若将此图像绕着原点O逆时针转90°，求出此图像的函数表达式．
【解析】解：（1）∵y－2与x+2成正比例，
∴设y－2=k（x+2）.
将x=1时，y=8代入得：8－2=k（1+2），解得：k=2
∴y与x之间的函数表达式为：y=2x+6
（2） ①列表，
y=2x+6的图像如下所示：
②图像如下所示：

由（2）①中表可知，A点坐标为（-3,0），B点坐标为（0,6）
∵将函数y=2x+6的图像绕着原点O逆时针转90°
∴A绕原点旋转后的对应点A1的坐标为：（0，-3），B绕原点旋转后的对应点B1的坐标为：（-6，0）
设旋转后的图像表达式为：y=ax＋b
将A1、B1的坐标代入得：
−3=b0=−6a+b
解得：a=−12b=−3
∴此图像的函数表达式为：y=−12x−3
2．请你用学习“一次函数”中积累的经验和方法研究函数y=2|x|−2的图像和性质，并解决问题．
(1)①当x=0时，y=2|x|−2=−2；
②当x>0时，y=2|x|−2＝ ；
③当x<0时，y=2|x|−2＝ ；
显然，②和③均为某个一次函数的一部分．
(2)在平面直角坐标系中，作出函数y=2|x|−2的图像．
(3)根据函数图像写出函数y=2|x|−2的一条性质： ．
(4)一次函数y=kx+b（k为常数，k≠0）的图像过点(1,−3)，若y=kx+by=2x−2无解，结合函数的图像，直接写出k的取值范围．
【解析】（1）②∵x>0时，|x|=x，
∴x>0时，y=2|x|−2=2x−2，
③∵x<0时，|x|=−x，
∴x<0时，y=2|x|−2=−2x−2，
故答案为：2x−2，−2x−2．
（2）当x=0时，y=2|x|−2=−2；
当y=0时，x=±1．
如图，
（3）由图像可得，函数图像关于y轴对称，
故答案为：函数图像关于y轴对称．
（4）当k>0时，如图，当直线y=kx+b与y=2x−2时，方程无解，此时k=2，
∴当0如图，当直线经过(1,−3)，(0,−2)时，
将(1,−3)，(0,−2)代入y=kx+b得−3=k+b−2=b，
解得k=−1b=−2，
∴−1综上所述，若y=kx+by=2x−2无解时，−1x
−2
−1
1
2
y
12
10
8
4
x
⋯
-2
-1
0
1
2
⋯
y=2x-3
⋯
⋯
x
⋯
-2
-1
0
1
2
⋯
y=2x-3
⋯
-7
-5
-3
-1
1
⋯
x
-3
0
y
0
6