初中数学苏科版八年级上册6.3 一次函数的图像测试题

这是一份初中数学苏科版八年级上册6.3 一次函数的图像测试题，文件包含63一次函数的图像2分层练习解析版docx、63一次函数的图像2分层练习docx等2份试卷配套教学资源，其中试卷共14页， 欢迎下载使用。

考查题型一 一次函数图像的识别
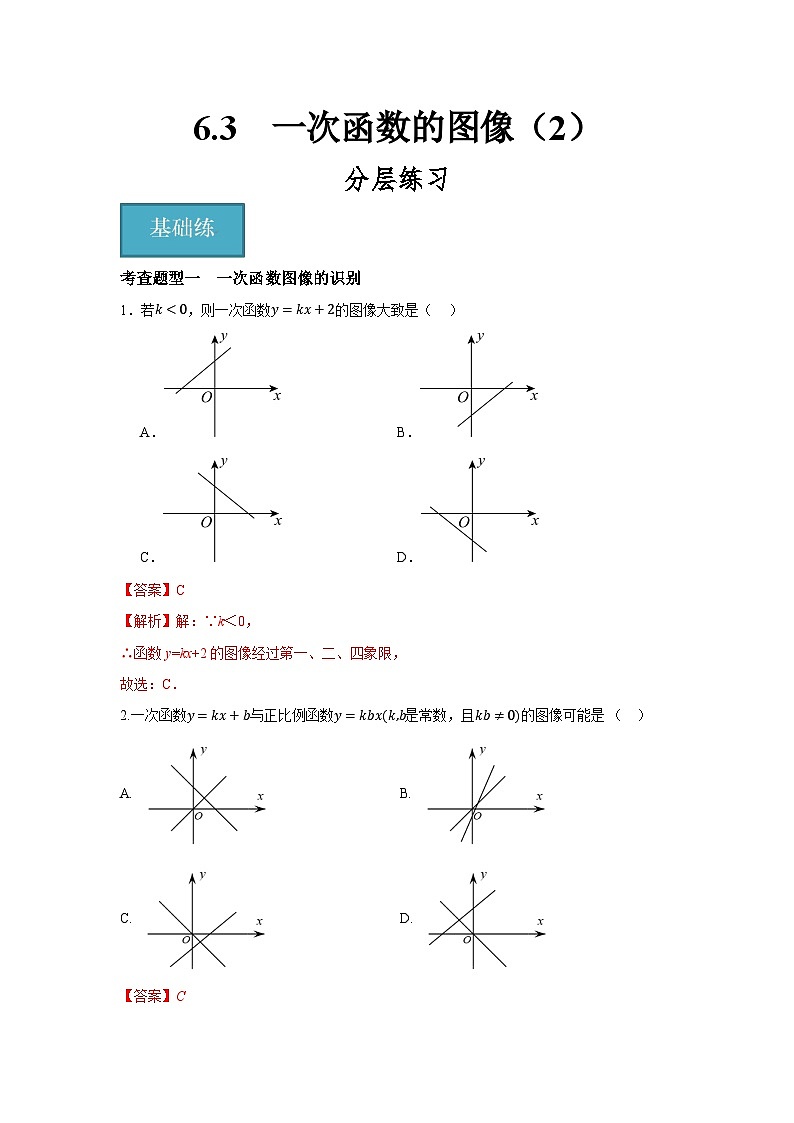
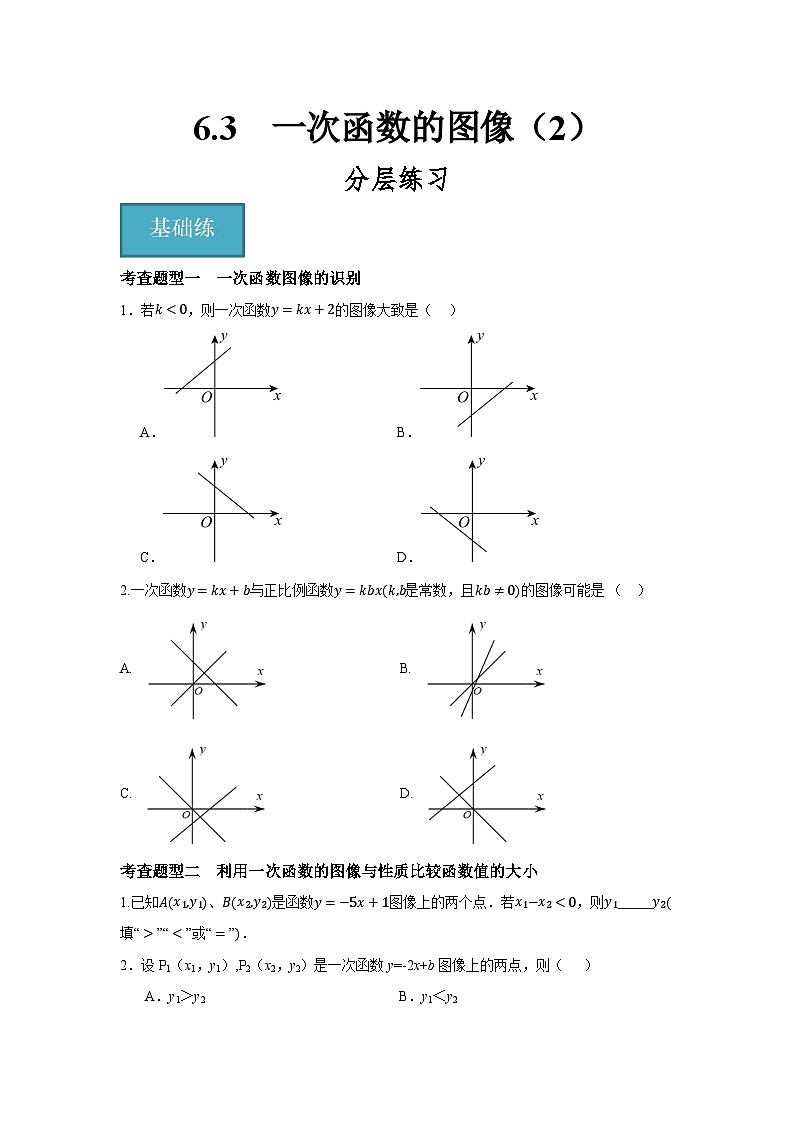
1．若k<0，则一次函数y=kx+2的图像大致是（ ）
A． B．
C． D．
【答案】C
【解析】解：∵k＜0，
∴函数y=kx+2的图像经过第一、二、四象限，
故选：C．
2.一次函数y=kx+b与正比例函数y=kbx(k,b是常数，且kb≠0)的图像可能是（ ）
A. B.
C. D.
【答案】C
【解析】解：①当kb>0，正比例函数y=kbx过第一、三象限；k与b同号，当k，b同正时，y=kx+b的图像过第一、二、三象限；当k，b同负时，y=kx+b的图像过第二、三、四象限，故A、B两选项错误；
②当kb<0时，正比例函数y=kbx过第二、四象限；k与b异号，k>0，b<0时y=kx+b过第一、三、四象限；k<0，b>0时过第一、二、四象限，故C选项正确，D选项错误．
故选C．
考查题型二 利用一次函数的图像与性质比较函数值的大小
1.已知A(x1,y1)、B(x2,y2)是函数y=−5x+1图像上的两个点．若x1−x2<0，则y1 y2(填“>”“<”或“=”)．
【解析】∵k=−5<0，
∴y随x的增大而减小．
又∵点A(x1,y1)，B(x2,y2)是函数y=−5x+1图像上的两个点，且x1−x2<0，即x1∴y1>y2.
故答案为>．
2．设P1（x1，y1）,P2（x2，y2）是一次函数y=-2x+b图像上的两点，则（ ）
A．y1＞y2 B．y1＜y2
C．当x1＜x2时，y1＞y2D．当x1＜x2时，y1＜y2
【答案】C
【解析】∵一次函数y=-2x+b中，k=-2<0，
∴y随x的增大而减小，
∴当x1> x2时，y1< y2；当x1< x2时，y1> y2.
故选C.
考查题型三 利用一次函数的图像与性质求字母的值或取值范围
1．已知一次函数y=kx+b的图像如图所示，则k，b的取值范围是（ ）

A．k>0，b>0 B．k>0，b<0 C．k<0，b>0D．k<0，b<0
【答案】B
【解析】解：由图可知该一次函数图像经过第一、三、四象限，
则k>0，b<0．
故选：B．
2.若一次函数y=kx+5在−1≤x≤4的范围内有最大值17，则k的值为 ．
【解析】①若k<0，则当x=−1时，y有最大值17，
即−k+5=17，解得k=−12；
②若k>0，则当x=4时，y有最大值17，
即4k+5=17，解得k=3.
综上所述，k的值为−12或3．
3.已知函数y=(2m+1)x+m−3．
(1)若该函数的图像经过原点，求m的值．
(2)若该函数的图像与y轴的交点的纵坐标为−2，求m的值．
(3)若该函数的图像平行于直线y=3x−3，求m的值．
(4)若这个函数是一次函数，且y随着x的增大而减小，求m的取值范围．
【解析】(1)∵该函数的图像经过原点，
∴m-3＝0，解得m＝3．
(2)∵该函数的图像与y轴的交点的纵坐标为-2，
∴m-3＝-2，解得m＝1．
(3)∵该函数的图像平行于直线y＝3x-3，
∴2m+1＝3，解得m＝1．
(4)∵y随着x的增大而减小，
∴2m+1＜0，解得m<−12．
考查题型四 根据平移规律确定一次函数表达式
1．将直线y=2x向右平移1个单位后所得图像对应的函数表达式为（ ）
A．y=2x−2B．y=2x−1C．y=2x+1D．y=2x+2
【答案】A
【解析】解：将直线y=2x向右平移1个单位后所得图像对应的函数表达式为
y=2x−1=2x−2，
故选：A．
2.已知一次函数y=kx+b的图像经过点A(0,−3)和B(1,−1)，将该函数图像沿着x轴向右平移3个单位，再向下平移7个单位得到的函数表达式为 ．
【解析】解法一：将A(0,−3)，B(1,−1)，代入y=kx+b，
得b=−3,k+b=−1,解得k=2,b=−3.
∴一次函数的解析式为y=2x−3.
将y=2x−3的图像沿着x轴向右平移3个单位，再向下平移7个单位得到的函数表达式为y=2(x−3)−3−7=2x−16.
故答案为y=2x−16．
解法二：该函数图像沿着x轴向右平移3个单位，再向下平移7个单位后，
点A(0,−3)和B(1,−1)的对应点分别是A'(3,−10)和B'(4,−8)，
设经过点A'(3,−10)和B'(4,−8)的函数表达式为y=mx+n(m≠0).
把A'(3,−10)，B'(4,−8)代入，
得3m+n=−10,4m+n=−8,解得m=2,n=−16.
∴一次函数的解析式为y=2x−16．
考查题型五 一次函数的图像和性质的综合应用
1．关于一次函数y=kx+3k≠0，下列说法中正确的是（ ）
A．该函数的图像一定不经过第一象限
B．当k=2时，若x的取值增加2，则y的值也增加2
C．该函数的图像向下平移3个单位后一定经过坐标原点
D．若该函数的图像与两坐标轴所围成的三角形面积是92，则k=1
【答案】C
【解析】解：一次函数y=kx+3k≠0，当x=0时，y=3，
∴图像经过0,3，
∴图像一定经过第一象限，故A错误，不合题意；
当k=2时，y=2x+3，
若x的取值增加2，则2x+2+3−2x+3=4，
即y值增加4，故B错误，不合题意；
该函数的图像向下平移3个单位后，得y=kx+3−3=kx，为正比例函数，
则必经过原点，故C正确，符合题意；
在y=kx+3k≠0中，令x=0，则y=3，令y=0，则x=−3k，
∴函数图像与坐标轴的交点为−3k,0，0,3，
∴−3k×3×12=92，
解得：k=1或k=−1，故D错误，不合题意；
故选：C．
2．甲、乙两位同学各给出某函数的一个特征，甲：“函数值y随自变量x增大而减小”；乙：“函数图像经过点(0，2)”，请你写出一个同时满足这两个特征的函数，其表达式是 ．
【答案】y=−2x+2（答案不唯一）
【解析】解：根据题意，甲：“函数值y随自变量x增大而减小”；
可设函数为：y=−2x+b,
又满足乙：“函数图像经过点(0，2)”，
则函数表达式为y=−2x+2，
故答案为：y=−2x+2（答案不唯一）
考查题型六 一次函数与几何图形的综合应用
1．平面直角坐标系中，平行四边形OABC的边OC在x轴的正半轴，点C(4，0)，B(6，2)，直线y=2x+1以每秒1个单位的速度向下平移，经过 秒，该直线将平行四边形OABC面积平分．
【答案】6
【解析】解：连接AC、BO，交于点D，当y=2x+1经过D点时，该直线可将平行四边形OABC的面积平分；
∵四边形OABC是平行四边形，
∴BD=OD.
∵B(6，2)，
∴D(3，1).
∵直线DE平行于y=2x+1，
∴设DE的解析式为y=2x+b.
∵过D(3，1)，
∴1=2×3+b，
∴b=−5，
∴DE的解析式为y=2x−5，
∴直线y=2x+1要向下平移6个单位，
∴时间为6秒，
故答案为：6．
2．如图，一次函数y=kx+bk≠0的图像经过点A、B．

(1)根据图像，求一次函数y=kx+bk≠0的表达式；
(2)将直线AB向下平移5个单位后经过点m,−5，求m的值．
(3)P0,a为y轴上的一动点，当△ABP的面积为15时，求a的值．
【解析】（1）解：由题意可得，A(2,6)，B(−4,−3)，
将点A,B的坐标代入y=kx+bk≠0，
可得6=2k+b−3=−4k+b，解得k=32b=3，
∴该函数解析式为y=32x+3；
（2）将直线AB向下平移5个单位后得到y=32x+3−5，即y=32x−2，
∵经过点m,−5，
∴−5=32m−2，
解得m=−2；
（3）设该一次函数与y轴交于点C，如下图，

对于一次函数y=32x+3，
令x=0，则有y=3，
即C(0,3)，
根据题意，△ABP的面积为15，
则有S△ABP=123−a×[2−(−4)]=15，
即3−a=5，
∴3−a=±5，
解得a=−2或8．
1.如图，在平面直角坐标系中，有A(0,1)、M(3,2)、N(4,4)三点．动点P从点A出发，沿y轴以每秒1个单位长度的速度向上移动，且过点P的直线l：y=−x+b也随之移动．设移动的时间为t s．
(1)当t=2时，AP= ，此时点P的坐标是 ．
(2)当t=3时，求直线l对应的函数表达式．
(3)当直线l：y=−x+b从经过点M到经过点N时，求点P向上移动的时间．
(4)当点Q在x轴上时，若S△ONQ=8，则点Q的坐标为 ．
【解析】(1)2;(0，3)
(2)∵t＝3，
∴AP＝1×3＝3．
∴OP＝OA+AP＝1+3＝4．
∴点P的坐标是(0，4)．
把(0，4)代入y＝-x+b，得b＝4，
∴直线l对应的函数表达式为y＝-x+4．
(3)当直线y＝-x+b经过点M(3，2)时，-3+b＝2，解得b＝5．
∴y＝-x+5． 令x＝0，则y＝5．
∴AP＝OP-OA＝5-1＝4．
∴t=41=4．
当直线y＝-x+b经过点N(4，4)时， -4+b＝4，解得b＝8．
∴y＝-x+8． 令x＝0，则y＝8．
∴AP＝OP-OA＝8-1＝7．
∴t=71=7．
∵7-4＝3(s)，
∴点P向上移动了3 s．
(4)(4，0)或(-4，0)．
2.如图，在平面直角坐标系中，点A，A1，A2，…在x轴上，分别以OA，AA1，A1A2，…为边在第一象限作等边△OAP，等边△AA1P1，等边△A1A2P2，…，且A点坐标为(2 3,0)，直线y=kx+32(k>0)经过点P，P1，P2，…，则点P2022的纵坐标为 ．
【解析】解：过点P作PD⊥ x 轴于点D，
∵等边△OAP，且A点坐标为(2 3 ，0)，
∴OA= OP=2 3 ，OD=DA= 3 ，∠POD=60°，
∴PD= OP2+OD2= 3，
∴P点坐标为( 3 ，3)，
∵直线y=kx+ 32 (k>0)经过点P，
∴3= 3 k+ 32 ，
解得：k= 32 ，
∴直线的解析式为y= 32 x+ 32 ，
过点P1作PE⊥ x 轴于点E，
设P1点坐标为 (x， 32 x+ 32 )，
∴AE=x−2 3 ，P1E= 32 x+ 32 ，
∵∠P1AE=60°，∠AP1E=30°，
∴P1E= 3 AE，
∴ 32 x+ 32 = 3 (x−2 3 )，
解得：x=5 3 ，
∴P1点的纵坐标为9=32，
同理，P2点的纵坐标为27=33，
⋯ ，
∴点P2022的纵坐标为32023．
故答案为：32023．