2024河南中考数学专题复习第三章 微专题 二次函数与直线、线段的交点问题 课件

这是一份2024河南中考数学专题复习第三章 微专题 二次函数与直线、线段的交点问题 课件，共20页。PPT课件主要包含了例1题图，例1题解图，第1题图，第1题解图②，第1题解图③，b＞3，b＜3，第2题图①，数形结合，第2题图②等内容，欢迎下载使用。

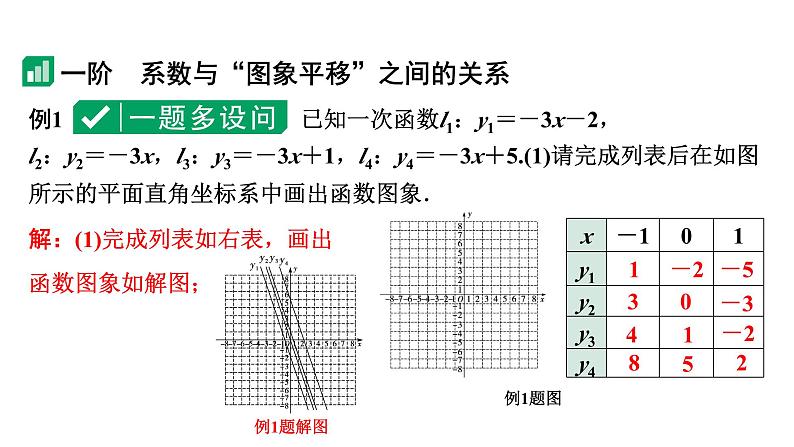
例1 已知一次函数l1：y1＝－3x－2，l2：y2＝－3x，l3：y3＝－3x＋1，l4：y4＝－3x＋5.(1)请完成列表后在如图所示的平面直角坐标系中画出函数图象．
【发现规律】①观察函数解析式特点，可以发现：一次函数L的解析式为y＝－3x＋m；②观察函数图象特点：可发现所作的函数图象都________；【规律总结】一次函数y＝－3x＋m，当m取不同值时，函数图象为 y＝－3x平移后的一系列平行直线．【方法应用】(2)已知y＝－3x＋2与y＝kx＋3平行，则k＝________．
【一般化结论】两个一次函数解析式中：k1＝k2，b1≠b2⇌两直线平行．
①直线y＝kx＋b(k≠0)可由直线y＝kx平移得到；②直线上对应点的连线平行．
类型一　定抛物线与动直线
1. 已知抛物线y＝－2x2＋x＋1.(1)如图①，若直线y＝m与该抛物线有一个交点，则m＝________；
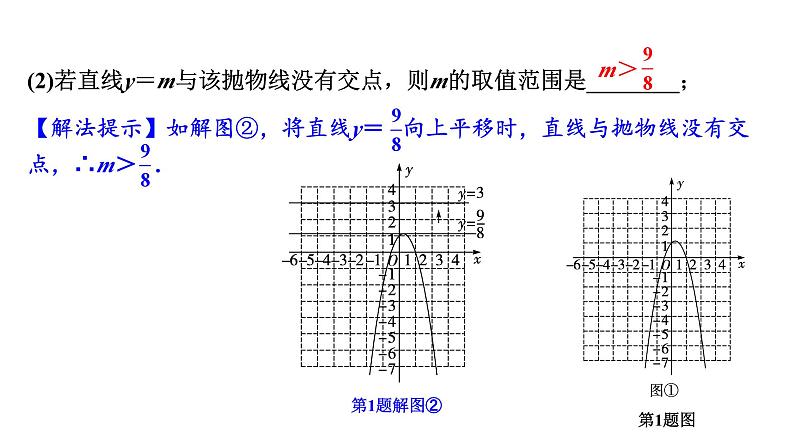
(2)若直线y＝m与该抛物线没有交点，则m的取值范围是________；
【解法提示】如解图②，将直线y＝ 向上平移时，直线与抛物线没有交点，∴m＞ .
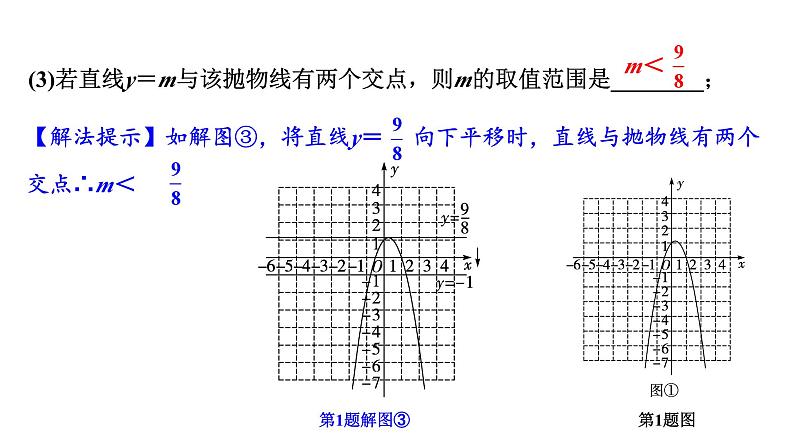
(3)若直线y＝m与该抛物线有两个交点，则m的取值范围是________；
【解法提示】如解图③，将直线y＝ 向下平移时，直线与抛物线有两个交点∴m＜
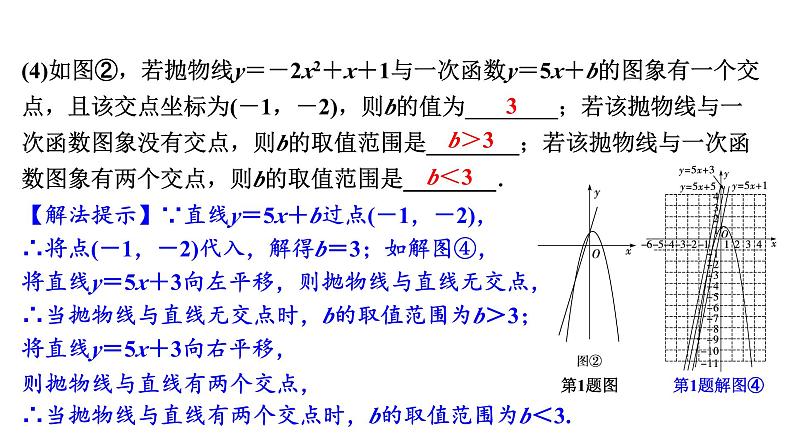
(4)如图②，若抛物线y＝－2x2＋x＋1与一次函数y＝5x＋b的图象有一个交点，且该交点坐标为(－1，－2)，则b的值为________；若该抛物线与一次函数图象没有交点，则b的取值范围是________；若该抛物线与一次函数图象有两个交点，则b的取值范围是________．
图解法判断抛物线与平行于x轴的直线y＝m的交点：如第1题图①直线y＝m与抛物线有一个交点即直线y＝m过抛物线的顶点，沿y轴向上平移，直线y＝m与抛物线没有交点，沿y轴向下平移，直线y＝m与抛物线有两个交点．
类型二　定抛物线与动线段
2. (线段在x轴上，位置不固定)已知抛物线y＝－x2－x＋2交x轴于点A和点B(点A在点B的左侧)，C(t，0)，D(t＋4，0)是x轴上的两点(点C在点D的左侧)．(1)情况一：如图①，若线段CD与抛物线无交点，则线段CD在点A左侧或线段CD在点B右侧，求t的取值范围；
解：(1)由题意知，点A，B的坐标分别为(－2，0)，(1，0)，∴AB＝3，∵点C，D的坐标分别为(t，0)，(t＋4，0)，∴CD＝4，根据题图①可知，t满足的条件为t＞1或t＋4＜－2， 即t的取值范围为t＞1或t＜－6；
(2)情况二：如图②，若线段CD与抛物线有一个交点，则点D在AB之间(点D可以与点A重合，但不可以与点B重合)或__________________________________________________，求t的取值范围；
点C在AB之间(点C可以与点B重合，但不可以与点A重合)
根据题图②可知，t满足的条件为－2≤t＋4＜1或－2＜t≤1，即t的取值范围为－6≤t＜－3或－2＜t≤1；
(3)情况三：如图③，若线段CD与抛物线有两个交点，则__________________________________________________________，求t的取值范围．
点C在点A左侧(可以与点A重合)且点D在点B右侧(可以与点B重合)
根据题图③可知，t满足的条件为t≤－2且t＋4≥1，即t的取值范围为－3≤t≤－2.
1. “找界点”—交点2. 线段在直线CD上，位置不固定，分三种情况：情况一：如图①，线段CD(CD≥AB)与抛物线无交点，则线段CD在点A所在与x轴平行的直线上方或线段CD在点B所在与x轴平行的直线下方；情况二：如图②，线段CD与抛物线有一个交点，则点C在AB之间(点C可以与点B重合)或点D在AB之间(点D可以与点A重合)；
情况三：如图③，线段CD与抛物线有两个交点，点C在点A所在与x轴平行的直线上方(点C可以与点A重合)，点D在点B所在与x轴平行的直线下方(点D可以与点B重合)．
3. (线段在直线上，位置不固定)已知直线y＝－ x－4与抛物线y＝x2＋ x－4交x轴负半轴于点A，交y轴负半轴于点B，C，D是直线y＝－ x－4上的两点(点C在点D的左侧)，且CD＝10，若线段CD与抛物线有两个交点，求点C横坐标的取值范围．
如解图②，当点B与点D重合时，线段CD与抛物线仍有两个交点，
即t＋6＝0，解得t＝－6；若t＜－6，如解图③，线段CD与抛物线只有一个交点，∴当线段CD与抛物线有两个交点时，点C横坐标的取值范围为－6≤t≤－3.
4. (线段一端点在直线上，位置不固定)(2023.22考法) 已知抛物线y＝－x2－x＋2交x轴的负半轴于点A，交y轴正半轴于点B，点M是直线AB上的一个动点，将点M向左平移5个单位长度得到点N，若线段MN与该抛物线只有一个公共点，求点M的横坐标xM的取值范围．
如解图，当直线MN经过抛物线顶点时，线段MN与抛物线只有一个交点，令x＋2＝ ，解得x＝ ，∴若线段MN与该抛物线只有一个公共点时，此时xM＝ ；当点M与点B重合时，线段MN与该抛物线恰有两个交点，此时xM＝0；当点M与点A重合时，线段MN与该抛物线恰有一个交点，此时xM＝－2，∴点M的横坐标xM的取值范围为－2≤xM＜0或xM＝ .