2024河南中考数学专题复习第一章 第四节 分式 课件

这是一份2024河南中考数学专题复习第一章 第四节 分式 课件，共20页。PPT课件主要包含了课标要求，考情及趋势分析，分式的有关概念及性质，中含有字母，B≠0，A＝0且B≠0，不等于零的整式，分式的运算，加减运算，乘除运算等内容，欢迎下载使用。
命题点1　分式有意义的条件(2021.11 )
了解分式和最简分式的概念．
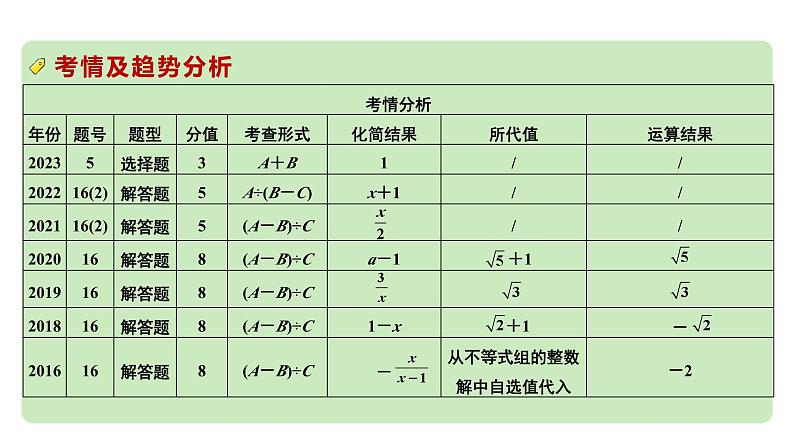
命题点2　分式的化简及求值(9年8考，仅2017年未考查)
1. 能用提公因式法、公式法(直接利用公式不超过二次)进行因式分解(指数是正整数)；2. 能利用分式的基本性质进行约分和通分；3. 能进行简单的分式加、减、乘、除运算．
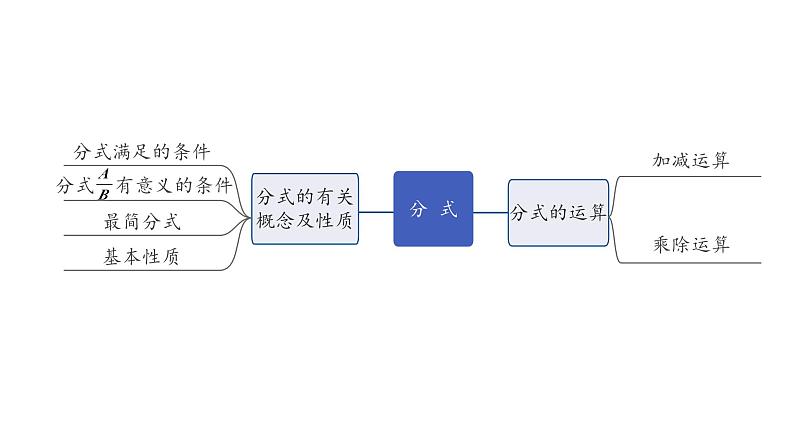
分式满足的条件（两个条件缺一不可）
1.形如 (A，B表示两个整式，B≠0)
分式 有意义的条件： 　　　　
分式 值为0的条件： 　　　　
最简分式：____________________________
分子和分母没有公因式的分式
基本性质：分式的分子与分母都乘(或除以)同一个　　　　　　　　，分式的值不变
＝ (C≠0) 通分
＝ (C≠0) 约分
同分母：分母不变，把分子相加减，即 ± ＝________
异分母：先通分，化为同分母的分式，然后再按同分母分式的加减法法则进行计算，即 ± 　　　　 　　　　(关键是通分)
通分 找最简公分母
1. 分母中能分解因式的，先分解因式
2. 取各分母所有因式的最高次幂的积(数字因式取它们的最小公倍数)作为公分母
知识关联整式的加减实质上是合并同类型；整式的乘法实际上是幂的运算；整式的除法实际上就是分式.
乘法： ＝　　　　(关键是约分)
除法： ÷ 　　　　 ________
约分 找公因式
1.分子、分母中能分解因式的，先分解因式2.取分子、分母中的相同因式的最低次幂的积(数字因式取它们的最大公约数)作为公因式
分式有意义的条件 2021.11
1. (2021河南11题3分)若代数式 有意义，则实数x的取值范围是________．
分式的化简及求值 9年8考，仅2017年未考查
2. 化简：1－ .　　　　　　
解：原式＝ － ＝ .
解：原式＝ ＋ ＝ .
3. 化简： ＋ .
解：原式＝ · ＝－a.
4. 化简： · .
5. 化简： ÷ .
类型一　分式的化简 (9年3考)
6. (2023河南5题3分)化简 ＋ 的结果是(　　)
A. 0B. 1C. aD. a－2
7. [2022河南16(2)题5分]化简： ÷(1－ )．
解：原式＝ ÷( － ) ＝ ÷ (3分) ＝ · ＝ · ＝x＋1.(5分)
8. [2021河南16(2)题5分]化简：(1－ )÷ .
类型二　分式的化简求值—确定值代入 (9年4考)
9. (2023河南16题8分)先化简，再求值：(1－ ) ÷ ，其中a＝ ＋1.
解：原式＝ ÷ ＝ · (4分) ＝a－1.(6分) 当a＝ ＋1时，原式＝ ＋1－1＝ .(8分)
类型三　分式的化简求值—自选值代入
10. (2022河南16题8分)先化简，再求值：( －1)÷ ，其中x的值从不等式组 的整数解中选取.
解：原式＝ ÷ (3分) ＝ · ＝ .(5分) 解不等式组 ，得－1≤x＜ ，
∴不等式组的整数解有－1，0，1，2(7分) ，要使分式有意义，x只能取2，∴原式＝ ＝－2.(8分)
分式化简求值的一般步骤有：①通分；②同分母分式加减； ③分解因式；④除法变乘法；⑤约分；⑥代值求解．
1.化简求值类题一定要做到先“化简”，再“求值”，自身能约分的先自身约分；2.通分时，若有常数项，要记得把常数项化成分母为最简公分母的分式，再进行加减运算；3.分式化简求值时，要注意符号的变化，分式的分子要作为一个整体，在添括号或去括号时，若括号前为负号则去括号后括号内每一项都要变号；4.注意化简结果应为最简分式或整式