2024河南中考数学专题复习第四章 第六节 课时1 可解三角形 课件

这是一份2024河南中考数学专题复习第四章 第六节 课时1 可解三角形 课件，共14页。PPT课件主要包含了可解三角形，锐角三角函数，图表记忆法，例1题图①，例1题图②，例1题图③，例2题图等内容，欢迎下载使用。
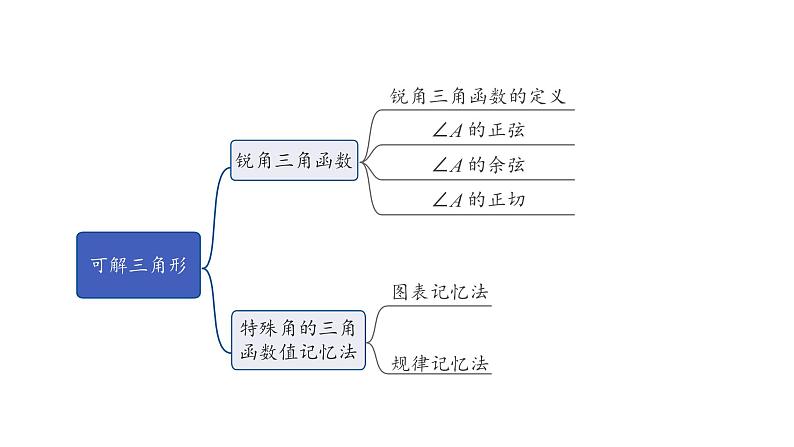
锐角三角函数的定义：在Rt△ABC中，∠C＝90°，∠A为△ABC中的一个锐角，则有：∠A的正弦：sin A＝______∠A的余弦：cs A＝______∠A的正切：tan A＝______
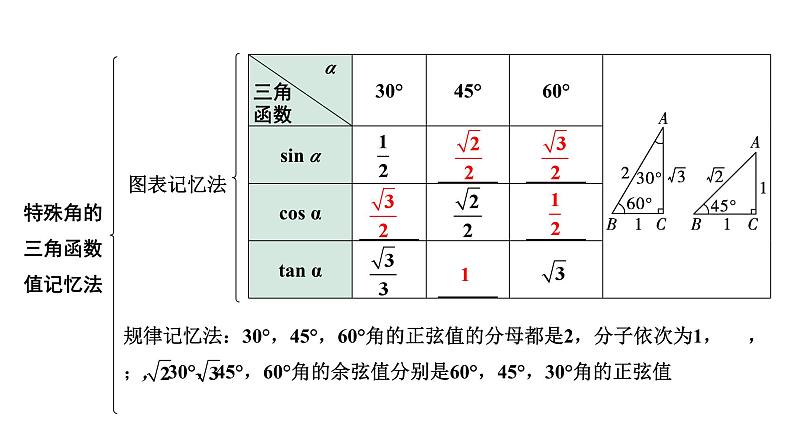
特殊角的三角函数值记忆法
规律记忆法：30°，45°，60°角的正弦值的分母都是2，分子依次为1， ， ；, 30°，45°，60°角的余弦值分别是60°，45°，30°角的正弦值
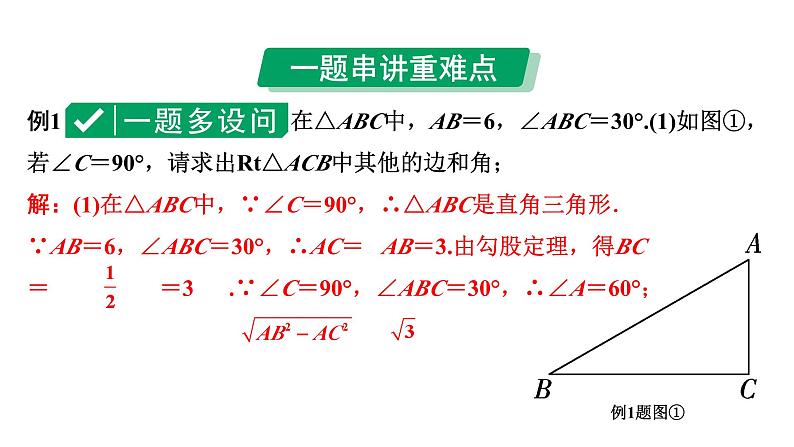
例1　 在△ABC中，AB＝6，∠ABC＝30°.(1)如图①，若∠C＝90°，请求出Rt△ACB中其他的边和角；
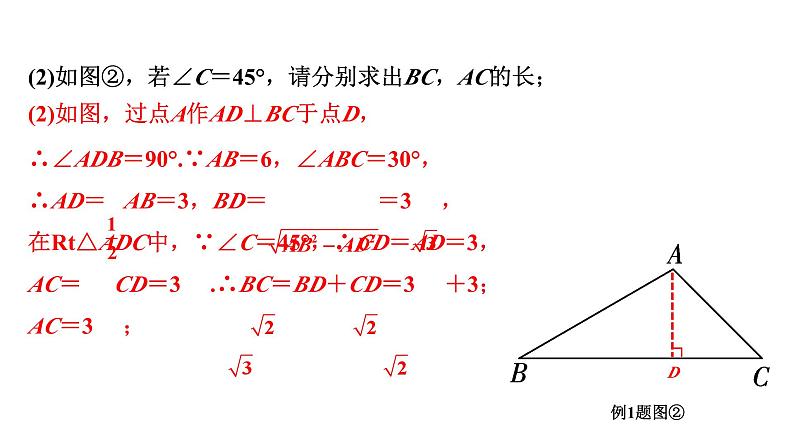
(2)如图②，若∠C＝45°，请分别求出BC，AC的长；
(2)如图，过点A作AD⊥BC于点D，
(3)如图③，若BC＝2 ，请分别求出AC的长和∠A的度数．
(3)如图，过点C作CD⊥AB于点D，
1. 三角形的三个内角和三条边，这六个条件如果已知其中任意三个条件(至少有一条边)，那么这个三角形可解．2. 若三角形为一般三角形，可将一般三角形作高线转化为直角三角形求解．
例2　 如图，在Rt△ABC中，∠BAC＝90°，过点A作AD⊥BC于点D.(1)AB＝6，BD＝3 ，求其他线段的长；
(2)AB＝6，BC＝4 ，求其他线段的长；
(3)AB＝6，CD＝ ，求其他线段的长．
射影定理—经典图形图中六条线段，知2求4，除了用到勾股定理外，可通过锐角三角函数解决，也可通过相似三角形解决．