
2024辽宁中考数学二轮中考考点研究 微专题 对称性质在折叠问题中的应用 (课件)
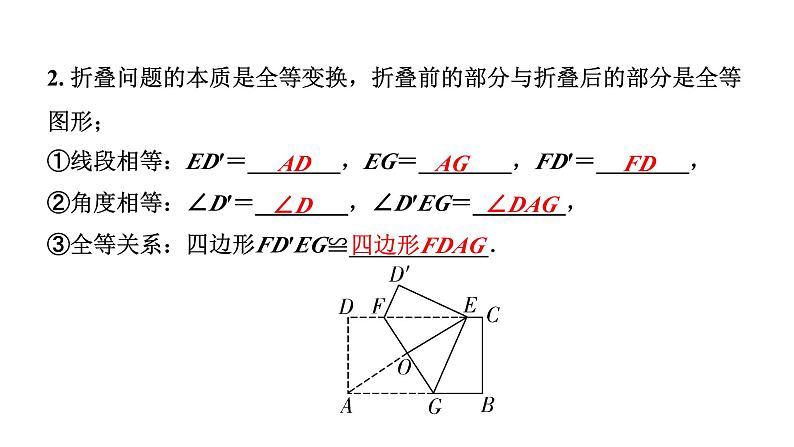
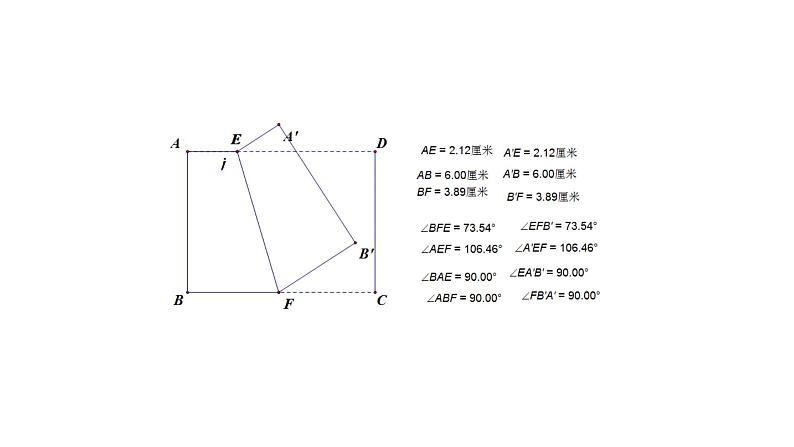
展开2. 折叠问题的本质是全等变换,折叠前的部分与折叠后的部分是全等图形;①线段相等:ED′=________,EG=________,FD′=________,②角度相等:∠D′=________,∠D′EG=________,③全等关系:四边形FD′EG≌____________.
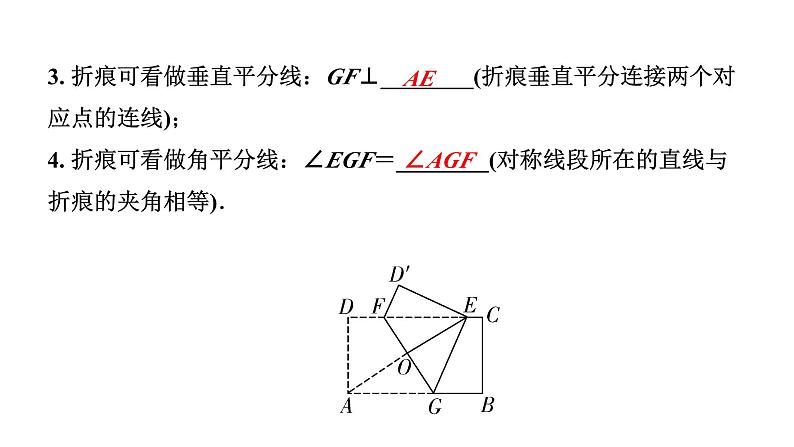
3. 折痕可看做垂直平分线:GF⊥________(折痕垂直平分连接两个对应点的连线);4. 折痕可看做角平分线:∠EGF=________(对称线段所在的直线与折痕的夹角相等).
(1)折叠方式确定,不需分类讨论,常用到的解题方法有:①勾股定理;②相似;③三角函数;④等面积法;(2)折叠中的动点问题常结合题设条件确定出满足条件情况,画出图形,求值.
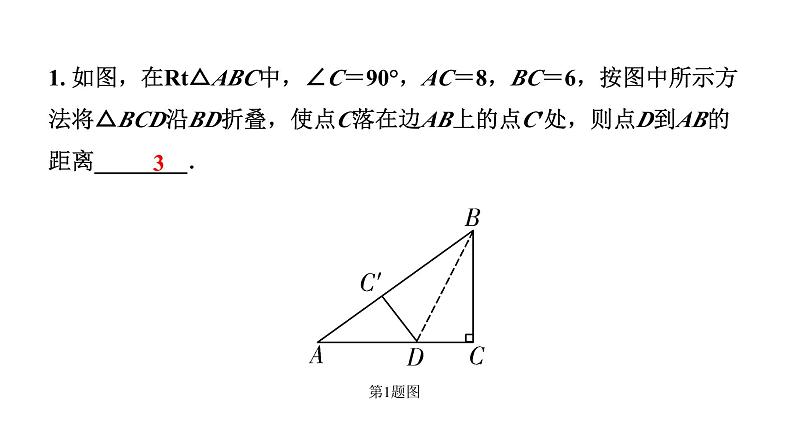
1. 如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,按图中所示方法将△BCD沿BD折叠,使点C落在边AB上的点C′处,则点D到AB的距离________.
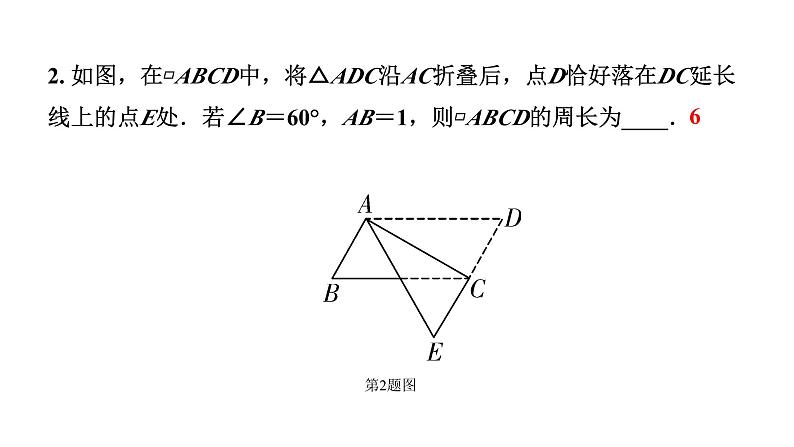
2. 如图,在▱ABCD中,将△ADC沿AC折叠后,点D恰好落在DC延长线上的点E处.若∠B=60°,AB=1,则▱ABCD的周长为____.
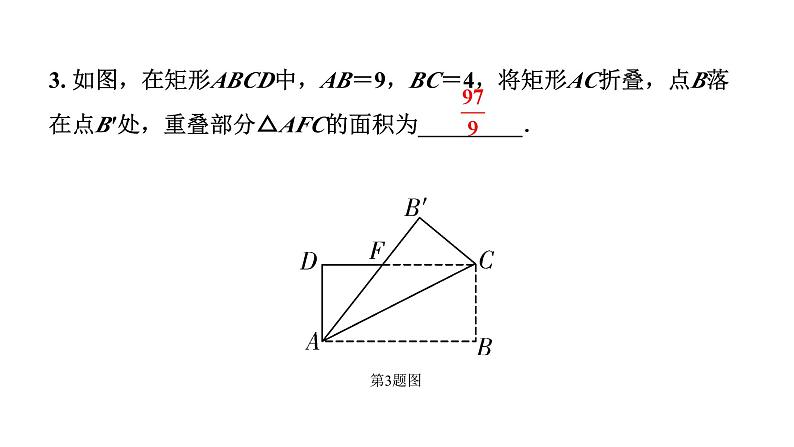
3. 如图,在矩形ABCD中,AB=9,BC=4,将矩形AC折叠,点B落在点B′处,重叠部分△AFC的面积为_________.
4. 如图,矩形纸片ABCD中,AB=4,BC=8,将矩形纸片ABCD折叠,使点C与点A重合,则折痕EF的长度为________.
5. 如图,E,F为正方形ABCD中BC,AD边上的中点,将正方形ABCD沿过点D的直线折叠,使得点A恰好落在EF上,记为A′,折痕GD交AB于点G,交EF于点H,则sin∠A′HG的值为________.
6. 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=9,点D为BC边上的中点,将△ACD沿AD对折,使点C落在同一平面内的点C′处,连接AB,BC′,则BC′的长为________.
7. 如图,在Rt△ABC中,∠BAC=90°,AB=4,AC=3,点D,E分别为AB,AC的中点,点P为BC边上一动点,将△BPD沿着DP翻折得到△FPD,连接DE,EF.若∠FDE=90°,则BP的长为_____.
8. 如图,在矩形ABCD中,AB=1,BC= ,点E在CD边上,连接AE,将四边形ABCE沿AE翻折,得到四边形AB′C′E,点B、C的对应点分别为点B′、C′.当B′C′恰好经过点D时,CE的长为________.
9. 如图,在Rt△ABC中,∠ACB=90°,AC=5,BC=8,点D是边BC的中点,点E是边AB上的任意一点(点E不与点B重合),沿DE翻折△DBE使点B落在点F处,连接AF,则线段AF长的最小值是________.
10. 如图,在矩形ABCD中,AB=8,AD=6,点E为AB边上一点,BE=2 ,点F为BC边上一动点,将△BEF沿EF所在直线折叠,当点B的对应点B′恰好落在AD的垂直平分线上时,折痕FE的长为________.
11. 如图,矩形ABCD中,AB=3,BC=4,点E是AB边上一点,且AE=2,点F是边BC上的任意一点,把△BEF沿EF翻折,点B的对应点为G,连接AG,CG,则三角形AGC的面积的最小值为_______.
12. 如图,在菱形ABCD中,∠A=60°,AD=2 .点P为对角线AC上的一个动点,过P作EF⊥AC交CD于点E,交AB于点F,将△AEF沿EF折叠,点A的对应点恰好落在对角线AC上的点G处,若△CBG是等腰三角形时,则AP的长为__________.
13. 如图,在矩形ABCD中,E、F分别是边BC、AD上一点,沿EF将四边形CDFE向下折叠,点C、D分别落在点G、H处,点H在边AB上.若∠BHG=20°,则∠EFH的度数为________.
14. 如图,在菱形ABCD中,对角线AC,BD相交于点O,AC=8,BD=6,点E是边AD上一点,直线OE交BC于点F,将菱形沿直线EF折叠,点B的对应点为点B′,点A的对应点为点A′,若AE=2,则B′F的长为______.
15. (2023铁岭模拟)如图,在矩形ABCD中,点E,F分别在边BC和AD上,把该矩形沿EF折叠,使点B恰好落在边AD的点H处,已知矩形ABCD的面积为16 ,FH=2HD,则折痕EF的长为________.
1. 如图,在Rt△ABC中,∠BAC=90°,∠B=35°,AD是斜边BC上的中线,将△ACD沿AD对折,使点C落在点F处,线段DF与AB相交于点E,则∠FAE的度数为_______.
2. 如图,将▱ABCD沿EF对折,使点A落在点C处,若∠A=60°,AD=2,AB=4,则CE的长为________.
3. 如图,矩形ABCD中,点E在边AD上,连接BE,点F在线段BE上,且BF=2EF,折叠矩形纸片使点C恰好落在点F处,折痕为DG,若AB=3,则折痕DG的长为________.
4. 如图,在平行四边形纸片ABCD中,连接对角线AC,将△ADC沿AC折叠得到△AEC,EC交AB于点F,若BC=3,△BCF为等边三角形,则△AFC的面积为________.
5. 如图,△ABC为等腰直角三角形,AC=BC=2,将△ABC沿∠BAC的平分线折叠,点C落在AB边上的点E处,D为AB的中点,连接DC,与折痕AF交于点M,则DM的长是________.
2024辽宁中考数学二轮中考考点研究 7.3 图形的对称、平移与旋转 (课件): 这是一份2024辽宁中考数学二轮中考考点研究 7.3 图形的对称、平移与旋转 (课件),共47页。PPT课件主要包含了图形的对称,第6题图,第7题图,与折叠有关的计算,第8题图,第9题图,第10题图,第12题图,第13题图,第14题图等内容,欢迎下载使用。
2024海南中考数学二轮重点专题研究 微专题 对称性质在折叠问题中的应用(课件): 这是一份2024海南中考数学二轮重点专题研究 微专题 对称性质在折叠问题中的应用(课件),共20页。PPT课件主要包含了∠DAG,四边形FDAG,∠AGF,80°等内容,欢迎下载使用。
2024海南中考数学二轮复习 微专题 对称性质在折叠问题中的应用(课件): 这是一份2024海南中考数学二轮复习 微专题 对称性质在折叠问题中的应用(课件),共20页。PPT课件主要包含了∠DAG,四边形FDAG,∠AGF,80°等内容,欢迎下载使用。












