北师大版（2024）2 从立体图形到平面图形课文课件ppt

这是一份北师大版（2024）2 从立体图形到平面图形课文课件ppt，共26页。PPT课件主要包含了学习目标，课堂导入，从正面看，从上面看，从左面看，随堂练习等内容，欢迎下载使用。
1. 经历从不同方向观察物体的活动过程，初步体会从不同方向观察物体可能看到不同的图形，发展空间观念.2.能辨认从三个方向看到的物体的形状图，会画立方体及其简单组合体从三个方向看到的形状图.3.能够根据从三个方向看到的形状图描述基本的几何体或实物模型.
问题朗读下面的古诗，你能发现其中蕴含的数学道理吗?
从不同的方向观察同一物体，通常可以看到不同的图形.
《题西林壁》横看成岭侧成峰，远近高低各不同.不识庐山真面目，只缘身在此山中.
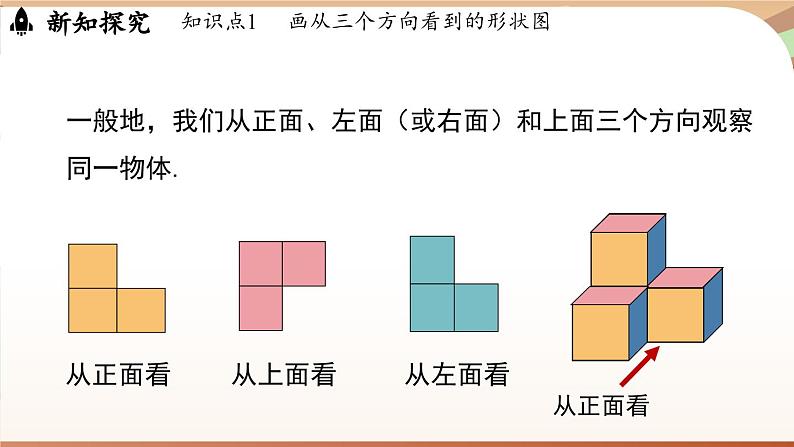
知识点1 画从三个方向看到的形状图
一般地，我们从正面、左面（或右面）和上面三个方向观察同一物体.
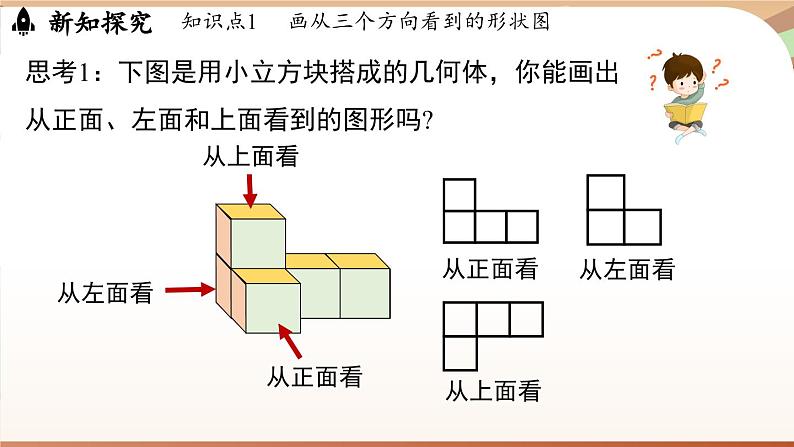
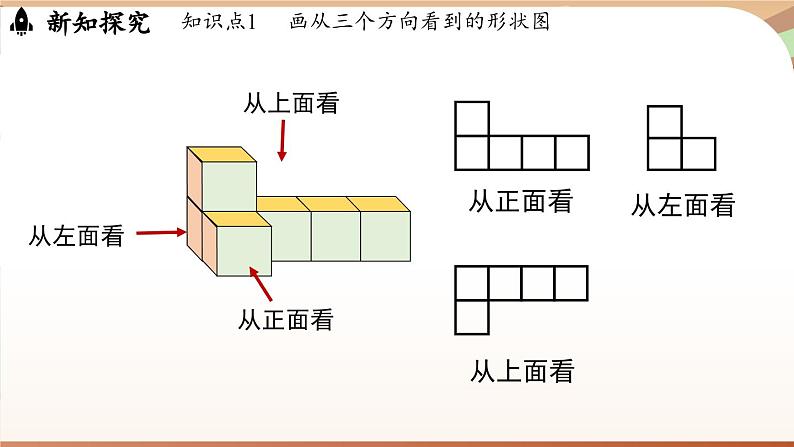
思考1：下图是用小立方块搭成的几何体，你能画出从正面、左面和上面看到的图形吗?
画从三个方向看小立方块的组合体的形状图的方法:①确定从三个方向看到的组合体的行数或列数;②确定每行或每列中小正方形的个数;③根据小正方形的个数及对应位置画出从三个方向看到的形状图.
例1 (1)用6个小立方块搭成不同的几何体，看能怎样搭?(2)分别画出所搭几何体从正面、左面、上面看到的形状图.
思考2：从正面、左面、上面观察几何体，形状如图所示，画出你所看到的几何体的形状图.
知识点2 由三个方向看到的形状图确定几何体
从三个方向看到的形状图与上下、前后、左右之间的关系:(1)正面的形状图：反映几何体的左右列数和每一列的上下层数.(2)左面的形状图：反映几何体的前后列数和每一列的上下层数.(3)上面的形状图：反映几何体的前后行数和每一行的左右列数.
思考3：从正面、左面、上面观察几何体，形状如图所示，画出你所看到的几何体的形状图.
分析:从正面看有3列，从左往右，每列上下的数量分别是1，2，1;从左面看有1列，这列上下的数量是2;从上面看有3列，从左往右，小方块的数量都是1，前后只有1行.
例2 如图，从正面看到的形状图和从上面看到的形状图对应的几何体可能是( )
解析:从正面看,几何体上下有两行,且上面一行只有中间一列有小正方体,排除C;从上面看,几何体前后有两行,且前面一行只有中间一列有小正方体,排除A,D.
例3 一个几何体由几个大小相同的小立方块搭成，从上面和从左面看到的这个几何体的形状图如图所示，请搭出满足条件的几何体．你搭的几何体由几个小立方块组成？
1.已知一个几何体由若干大小相同的小立方块搭成,如图所示,试画出从正面、左面和上面看到的几何体的形状图.
解析:从正面看有3列,从左到右每列小正方形的数目依次为3,2,1;从左面看有2列,从左到右每列小正方形的数目依次为3,1;从上面看有3列,从左到右每列小正方形的数目依次为2,1,1.
2. 下图是由一些相同的小立方块搭成的几何体从正面、左面、上面看到的形状图，组成这个几何体的小立方块的个数是( ) A.4个 B.5个 C.6个 D.7个
解析：根据题意搭出的几何体如图，故搭成这个几何体一共需要5个小立方块.
3.在仓库里堆放着若干个相同的小立方块货箱,仓库管理员将从三个方向看到的这些货箱的形状图画了出来，如图所示,则这堆货箱中小立方块货箱的个数为( ) A.9 B.10 C.11 D.12
解析:将从上面看到的形状图作为“地基”.由从正面看到的形状图可知,从上面看到的形状图中三列的小立方块的个数最多分别是1,3,1;由从左面看到的形状图可知,从上面看到的形状图中三行的小立方块的个数最多分别是3,2,1.因此,这堆货箱中小立方块的个数为1+1+2+3+1+1+1=10.
1 3 1
1 1
4. 一个几何体由大小相同的小立方块搭成,从上面看到的几何体的形状图如图所示,其中小正方形中的数字表示在该位置的小立方块的个数.请画出从正面和从左面看到的这个几何体的形状图.
解析：从正面看有3列,每列小立方块的数目从左到右分别为4，2，3.
解析：从左面看有3列,每列小立方块的数目从左到右分别为2，4，3.
5.一个几何体由若干大小相同的小立方块搭成,如图分别是从它的正面、上面看到的形状图,该几何体至少是用多少个小立方块搭成的?
思路引导：从正面看,确定上下层数,确定小立方块最少的个数;从上面看,确定底层个数,确定小立方块最少的个数.
解：由从上面看到的形状图可知,该几何体的底层一共有5个小立方块,结合从正面看到的形状图可知，从下到上第2层最多有3个小立方块,最少有1个小立方块,所以小立方块的个数最少为6.故该几何体至少是用6个小立方块搭成的.