

苏科版八年级数学上册同步考点必刷练精编讲义必刷提高练【1.1全等图形】(原卷版+解析)
展开1.1 全等图形
知识点01:全等形
的图形放在一起能够 叫做全等形.
知识要点:一个图形经过 后, 了,但 都没有改变,即 的图形全等.两个全等形的 .
一、选择题
1.(2020八上·禹州期中)下列四个图形中,有两个全等的图形,它们是( )
A.①和②B.①和③C.②和④D.③和④
2.(2020八上·蒙阴月考)下列说法中,正确的有( )
①正方形都是全等形;②等边三角形都是全等形;③形状相同的图形是全等形;④大小相同的图形是全等形;⑤能够完全重合的图形是全等形.
A.1个B.2个C.3个D.4个
3.下列说法正确的是( )
A.形状相同的两个图形一定全等B.两个长方形是全等图形
C.两个全等图形面积一定相等D.两个正方形一定是全等图形
4.下图所示的图形分割成两个全等的图形,正确的是( )
A.B.C.D.
5.(2019八上·景县期中)下列图形中与最右边图形全等的是( )
A.B.C.D.
6.(2018八上·邗江期中)规定:四条边对应相等,四个角对应相等的两个四边形全等.某学习小组在研究后发现判定两个四边形全等需要五组对应条件,于是把五组条件进行分类研究,并且针对二条边和三个角对应相等类型进行研究提出以下几种可能:① AB=A1B1,AD=A1D1,∠A=∠A1,∠B=∠B1,∠C=∠C1;② AB=A1B1,AD=A1D1,∠A=∠A1,∠B=∠B1,∠D=∠D1;③ AB=A1B1,AD=A1D1,∠B=∠B1,∠C=∠C1,∠D=∠D1;④ AB=A1B1,CD=C1D1,∠A=∠A1,∠B=∠B1,∠C=∠C1.其中能判定四边形ABCD和四边形A1B1C1D1全等有( )个
A.1B.2C.3D.4
7.(2018八上·前郭期中)下列说法正确的个数是( )
①面积相等的两个三角形全等;②两个等边三角形一定是全等图形;③如果两个三角形全等,它们的形状和大小一定都相同;④边数相同的图形一定能互相重合;⑤能够重合的图形是全等图形.
A.5B.4C.3D.2
8.如图所示,图中的两个三角形能完全重合,下列写法正确的是( )
A.△ABE≌△AFBB.△ABE≌△ABF
C.△ABE≌△FBAD.△ABE≌△FAB
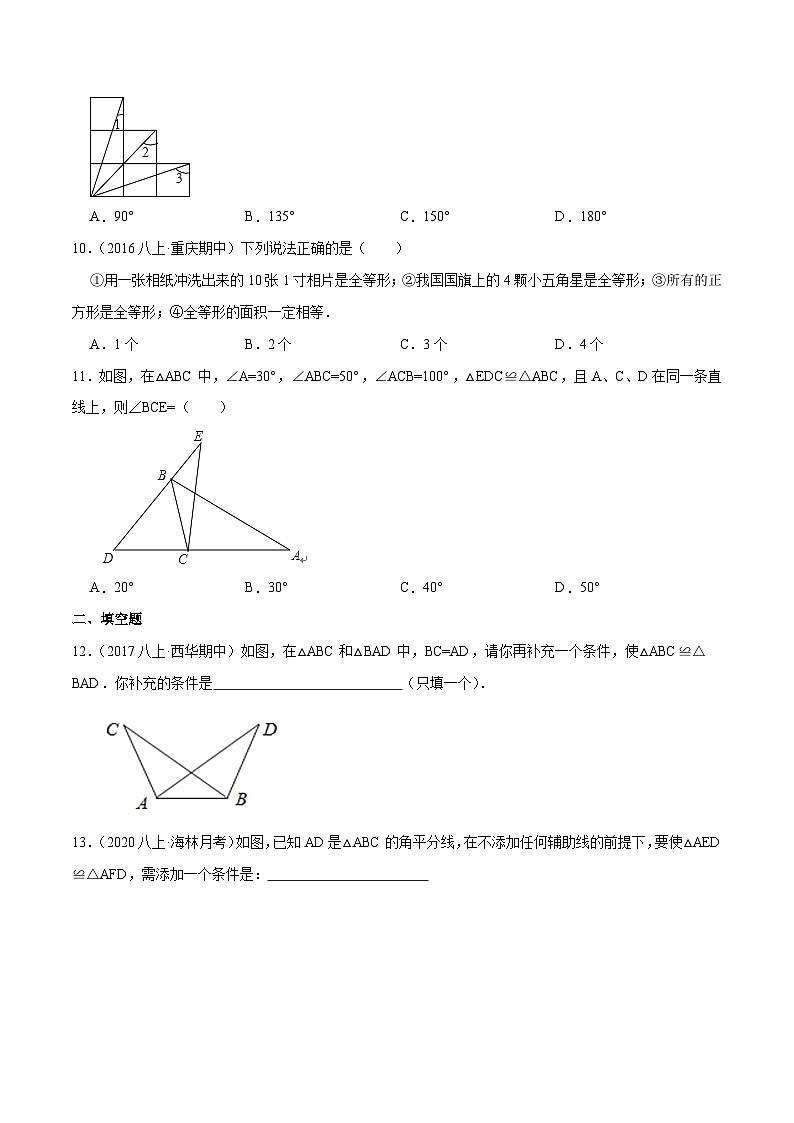
9.(2016八上·滨州期中)如图为6个边长相等的正方形的组合图形,则∠1+∠2+∠3=( )
A.90°B.135°C.150°D.180°
10.(2016八上·重庆期中)下列说法正确的是( )
①用一张相纸冲洗出来的10张1寸相片是全等形;②我国国旗上的4颗小五角星是全等形;③所有的正方形是全等形;④全等形的面积一定相等.
A.1个B.2个C.3个D.4个
11.如图,在△ABC中,∠A=30°,∠ABC=50°,∠ACB=100°,△EDC≌△ABC,且A、C、D在同一条直线上,则∠BCE=( )
A.20°B.30°C.40°D.50°
二、填空题
12.(2017八上·西华期中)如图,在△ABC和△BAD中,BC=AD,请你再补充一个条件,使△ABC≌△BAD.你补充的条件是 (只填一个).
13.(2020八上·海林月考)如图,已知AD是△ABC的角平分线,在不添加任何辅助线的前提下,要使△AED≌△AFD,需添加一个条件是:
14.(2019八上·丹东期中)如图,AE⊥AB,且AE=AB,BC⊥CD,且BC=CD,请按照图中所标注的数据,计算图中实线所围成的图形的面积S是
15.(2017八上·濮阳期中)如图,已知在△ABC中,∠A=90°,AB=AC,CD平分∠ACB,DE⊥BC于E,若BC=15cm,则△DEB的周长为 cm.
16.(2018八上·栾城期末)如图,已知等边△ABC中,BD=CE,AD与BE相交于点P,则∠APE的度数是 度.
17.如图,△ABC中,AB=AC,点D,E在BC边上,当 时,△ABD≌△ACE.(添加一个适当的条件即可)
18.(2021八上·仙桃月考)如图,△ABC 中,点 A(0,1),点 C(4,3),如果要使△ABD 与△ABC 全等,那么符合条件的点 D 的坐标为 .
三、解答题
19.如图,一块土地上共有20棵果树,要把它们平均分给四个小组去种植,并且要求每个小组分得的果树组成的图形、形状大小要相同,应该怎样分?
20.(2020八上·江苏月考)根据全等图形的定义,我们把能够完全重合(即四个内角、四条边分别对应相等)的四边形叫做全等四边形.请借助三角形全等的知识,解决有关四边形全等的问题.如图,已知,四边形 ABCD 和四边形 A'B'C'D'中,AB = A'B',BC = B'C',∠B = ∠B',∠C = ∠C',现在只需补充一个条件,就可得四边形 ABCD ≌四边形 A'B'C'D'. 下列四个条件:① ∠A = ∠A' ;② ∠D = ∠D' ;③ AD = A'D';④ CD = C'D'.
(1)其中,符合要求的条件是 .(直接写出编号)
(2)选择(1)中的一个条件,证明四边形 ABCD ≌四边形 A'B'C'D' .
2022-2023学年八年级数学上册考点必刷练精编讲义(苏科版)提高
第1章《全等三角形》
1.1 全等图形
知识点01:全等形
形状、大小相同的图形放在一起能够完全重合.能够完全重合的两个图形叫做全等形.
知识要点:一个图形经过平移、翻折、旋转后,位置变化了,但形状、大小都没有改变,即平移、翻折、旋转前后的图形全等.两个全等形的周长相等,面积相等.
一、选择题
1.下列四个图形中,有两个全等的图形,它们是( )
A.①和②B.①和③C.②和④D.③和④
【答案】B
【完整解答】解:①和③可以完全重合,因此全等的图形是①和③.
故答案为:B.
【思路引导】根据全等图形的概念进行判断.
2.下列说法中,正确的有( )
①正方形都是全等形;②等边三角形都是全等形;③形状相同的图形是全等形;④大小相同的图形是全等形;⑤能够完全重合的图形是全等形.
A.1个B.2个C.3个D.4个
【答案】A
【完整解答】解:正方形不一定都是全等形,故①不符合题意;
等边三角形不一定都是全等形,故②不符合题意;
形状相同的图形不一定都是全等形,故③不符合题意;
大小相同的图形不一定都是全等形,故④不符合题意;
能够完全重合的图形是全等形,故⑤符合题意;
故答案为:A.
【思路引导】由全等形:能够完全重合的图形是全等形,逐一判断各选项即可得到答案.
3.下列说法正确的是( )
A.形状相同的两个图形一定全等B.两个长方形是全等图形
C.两个全等图形面积一定相等D.两个正方形一定是全等图形
【答案】C
【完整解答】解:A.形状相同、大小相等的两个图形一定全等,A不符合题意;
B.长方形不一定是全等图形,B不符合题意;
C.两个全等图形面积一定相等,C符合题意;
D.两个正方形不一定是全等图形,D不符合题意;
故答案为:C.
【思路引导】直接利用全等图形以及全等图形的性质判断得出答案.
4.下图所示的图形分割成两个全等的图形,正确的是( )
A.B.C.D.
【答案】B
【完整解答】解:图形分割成两个全等的图形,如图所示:
故答案为:B.
【思路引导】直接利用全等图形的概念进而得出答案.
5.下列图形中与最右边图形全等的是( )
A.B.C.D.
【答案】B
【完整解答】解:与右边图形的全等的图形为B选项。
故答案为:B。
【思路引导】根据图形全等的含义即可得到答案。
6.规定:四条边对应相等,四个角对应相等的两个四边形全等.某学习小组在研究后发现判定两个四边形全等需要五组对应条件,于是把五组条件进行分类研究,并且针对二条边和三个角对应相等类型进行研究提出以下几种可能:① AB=A1B1,AD=A1D1,∠A=∠A1,∠B=∠B1,∠C=∠C1;② AB=A1B1,AD=A1D1,∠A=∠A1,∠B=∠B1,∠D=∠D1;③ AB=A1B1,AD=A1D1,∠B=∠B1,∠C=∠C1,∠D=∠D1;④ AB=A1B1,CD=C1D1,∠A=∠A1,∠B=∠B1,∠C=∠C1.其中能判定四边形ABCD和四边形A1B1C1D1全等有( )个
A.1B.2C.3D.4
【答案】C
【完整解答】有一组邻边和三个角对应相等的两个四边形全等,故①②③正确.
故答案为:C.
【思路引导】根据有一组邻边和三个角对应相等的两个四边形全等即可判断求解。
7.下列说法正确的个数是( )
①面积相等的两个三角形全等;②两个等边三角形一定是全等图形;③如果两个三角形全等,它们的形状和大小一定都相同;④边数相同的图形一定能互相重合;⑤能够重合的图形是全等图形.
A.5B.4C.3D.2
【答案】D
【完整解答】①面积相等的两个三角形不一定全等,不符合题意;②两个等边三角形一定是相似图形,但不一定全等,不符合题意;③如果两个三角形全等,它们的形状和大小一定都相同,符合全等形的定义,正确;④边数相同的图形不一定能互相重合,不符合题意;⑤能够重合的图形是全等图形,是全等三角形的概念,故正确,综上可得正确的说法有③⑤共2个.
故答案为:D.
【思路引导】全等三角形的面积一定相等,但面积相等的三角形不一定全等;两个等边三角形由于没有告诉其边的大小,故只能说它们的形状相同,即只能说明它们相似;能够重合的两个三角形全等,故如果两个三角形全等,它们的形状和大小一定都相同;要能重合的两个图形必须要它们的形状和大小一定都相同,边数相同的图形不一定大小形状相等,故也不一定能重合;根据全等形的定义,能够重合的图形是全等图形。
8.如图所示,图中的两个三角形能完全重合,下列写法正确的是( )
A.△ABE≌△AFBB.△ABE≌△ABF
C.△ABE≌△FBAD.△ABE≌△FAB
【答案】B
【完整解答】解:要把对应顶点写在对应位置.∵B和B对应,A和A对应,E和F对应,故△ABE≌△ABF.故答案为:B.
【思路引导】根据书写全等三角形的要求“把对应顶点写在对应位置”可判断。
9.如图为6个边长相等的正方形的组合图形,则∠1+∠2+∠3=( )
A.90°B.135°C.150°D.180°
【答案】B
【完整解答】解:如图,在△ABC和△DEA中,
,
∴△ABC≌△DEA(SAS),
∴∠1=∠4,
∵∠3+∠4=90°,
∴∠1+∠3=90°,
又∵∠2=45°,
∴∠1+∠2+∠3=90°+45°=135°.
故选B.
【思路引导】标注字母,利用“边角边”判断出△ABC和△DEA全等,根据全等三角形对应角相等可得∠1=∠4,然后求出∠1+∠3=90°,再判断出∠2=45°,然后计算即可得解.
10.下列说法正确的是( )
①用一张相纸冲洗出来的10张1寸相片是全等形;②我国国旗上的4颗小五角星是全等形;③所有的正方形是全等形;④全等形的面积一定相等.
A.1个B.2个C.3个D.4个
【答案】C
【完整解答】解:能够完全重合的两个图形叫做全等形.
①正确,用一张相纸冲洗出来的10张1寸相片,各相片可以完全重合,故是全等形;
②正确,我国国旗上的4颗小五角星是全等形;
③错误,所有的正方形边长不一定一样,故不能完全重合,不能称都是全等形;
④正确,全等形可以完全重合,故其面积一定相等.
∴共有三个正确,故选C.
【思路引导】根据全等形是能够完全重合的两个图形进行分析判断.
11.如图,在△ABC中,∠A=30°,∠ABC=50°,∠ACB=100°,△EDC≌△ABC,且A、C、D在同一条直线上,则∠BCE=( )
A.20°B.30°C.40°D.50°
【答案】A
【完整解答】解:∵△EDC≌△ABC,
∴∠DCE=∠ACB=100°,
∵A、C、D在同一条直线上,
∴∠ACD=180°,
∴∠BCE=∠ACB+∠DCE﹣∠ACD=20°,
故选A.
【思路引导】根据全等三角形的性质得到∠DCE=∠ACB=100°,由A、C、D在同一条直线上,得到∠ACD=180°,根据角的和差即可得到结论.
二、填空题
12.如图,在△ABC和△BAD中,BC=AD,请你再补充一个条件,使△ABC≌△BAD.你补充的条件是 (只填一个).
【答案】AC=BD(或∠CBA=∠DAB)
【完整解答】解:欲证两三角形全等,已有条件:BC=AD,AB=AB,
所以补充两边夹角∠CBA=∠DAB便可以根据SAS证明;
补充AC=BD便可以根据SSS证明.
故补充的条件是AC=BD(或∠CBA=∠DAB).
故答案是:AC=BD(或∠CBA=∠DAB).
【思路引导】根据已知条件在三角形中位置结合三角形全等的判定方法寻找条件.已知给出了一边对应相等,由一条公共边,还缺少角或边,于是答案可得.
13.如图,已知AD是△ABC的角平分线,在不添加任何辅助线的前提下,要使△AED≌△AFD,需添加一个条件是:
【答案】AE=AF或∠EDA=∠FDA
【完整解答】解:①添加条件:AE=AF,
证明:在△AED与△AFD中,
∵AE=AF,∠EAD=∠FAD,AD=AD,
∴△AED≌△AFD(SAS),
②添加条件:∠EDA=∠FDA,
证明:在△AED与△AFD中,
∵∠EAD=∠FAD,AD=AD,∠EDA=∠FDA,
∴△AED≌△AFD(ASA).
故答案为:AE=AF或∠EDA=∠FDA
【思路引导】要证两三角形全等的判定,已经有∠EAD=∠FAD,AD=AD,所以再添加一对边或一对角相等即可得证.
14.如图,AE⊥AB,且AE=AB,BC⊥CD,且BC=CD,请按照图中所标注的数据,计算图中实线所围成的图形的面积S是
【答案】50
【完整解答】解:∵AE⊥AB且AE=AB,EF⊥FH,BG⊥FH⇒∠FED=∠EFA=∠BGA=90°,
∠EAF+∠BAG=90°,∠ABG+∠BAG=90°⇒∠EAF=∠ABG,
∴AE=AB,∠EFA=∠AGB,∠EAF=∠ABG⇒△EFA≌△ABG
∴AF=BG,AG=EF.
同理证得△BGC≌△DHC得GC=DH,CH=BG.
故FH=FA+AG+GC+CH=3+6+4+3=16
故S=(6+4)×16﹣3×4﹣6×3=50.
故答案为50.
【思路引导】由AE⊥AB,EF⊥FH,BG⊥AG,可以得到∠EAF=∠ABG,而AE=AB,∠EFA=∠AGB,由此可以证明 △EFA≌△ABG,所以AF=BG,AG=EF;同理证得△BGC≌△DHC,GC=DH,CH=BG,故 FH=FA+AG+GC+CH=3+6+4+3=16,然后利用面积的割补法和面积公式即可求出图形的面积.
15.如图,已知在△ABC中,∠A=90°,AB=AC,CD平分∠ACB,DE⊥BC于E,若BC=15cm,则△DEB的周长为 cm.
【答案】15
【完整解答】解:∵CD平分∠ACB
∴∠ACD=∠ECD
∵DE⊥BC于E
∴∠DEC=∠A=90°
∵CD=CD
∴△ACD≌△ECD
∴AC=EC,AD=ED
∵∠A=90°,AB=AC
∴∠B=45°
∴BE=DE
∴△DEB的周长为:DE+BE+BD=AD+BD+BE=AB+BE=AC+BE=EC+BE=BC=15cm.
【思路引导】先根据ASA判定△ACD≌△ECD得出AC=EC,AD=ED,再将其代入△DEB的周长中,通过边长之间的转换得到,周长=BD+DE+EB=BD+AD+EB=AB+BE=AC+EB=CE+EB=BC,所以为15cm.
16.如图,已知等边△ABC中,BD=CE,AD与BE相交于点P,则∠APE的度数是 度.
【答案】60
【完整解答】解:∵等边△ABC,
∴∠ABD=∠C,AB=BC,
在△ABD与△BCE中,,
∴△ABD≌△BCE(SAS),
∴∠BAD=∠CBE,
∵∠ABE+∠EBC=60°,
∴∠ABE+∠BAD=60°,
∴∠APE=∠ABE+∠BAD=60°,
∴∠APE=60°.
故答案为:60.
【思路引导】根据题目已知条件可证△ABD≌△BCE,再利用全等三角形的性质及三角形外角和定理求解.
17.如图,△ABC中,AB=AC,点D,E在BC边上,当 时,△ABD≌△ACE.(添加一个适当的条件即可)
【答案】BD=CE
【完整解答】解:BD=CE,
理由是:∵AB=AC,
∴∠B=∠C,
在△ABD和△ACE中
∴△ABD≌△ACE(SAS),
故答案为:BD=CE.
【思路引导】根据等边对等角得出∠B=∠C,根据全等三角形的判定推出即可.
18.如图,△ABC 中,点 A(0,1),点 C(4,3),如果要使△ABD 与△ABC 全等,那么符合条件的点 D 的坐标为 .
【答案】 或 或(-1,3)
【完整解答】解:因为 与 的一条边 重合
当点D在 的下方时,满足条件的坐标有 和 ;
当点D在 的上方时,满足条件的坐标是 .
故满足条件的为 或 或(-1,3)
【思路引导】两个全等的图形,可以通过对折、旋转和平移得到,将△ABC沿AB翻折,得到一个点D1(4,-1),将△ABC旋转,使得AB与BA重合,得到一个点D2(-1,-1),将这个三角形再沿AB翻折,得到第三个点D3(-1,3),即可得出答案.
三、解答题
19.如图,一块土地上共有20棵果树,要把它们平均分给四个小组去种植,并且要求每个小组分得的果树组成的图形、形状大小要相同,应该怎样分?
【答案】解:如图所示:
【思路引导】根据能够完全重合的两个图形是全等形可求解,204=5,即可知,每一块试验田中有5棵树。
20.根据全等图形的定义,我们把能够完全重合(即四个内角、四条边分别对应相等)的四边形叫做全等四边形.请借助三角形全等的知识,解决有关四边形全等的问题.如图,已知,四边形 ABCD 和四边形 A'B'C'D'中,AB = A'B',BC = B'C',∠B = ∠B',∠C = ∠C',现在只需补充一个条件,就可得四边形 ABCD ≌四边形 A'B'C'D'. 下列四个条件:① ∠A = ∠A' ;② ∠D = ∠D' ;③ AD = A'D';④ CD = C'D'.
(1)其中,符合要求的条件是 .(直接写出编号)
(2)选择(1)中的一个条件,证明四边形 ABCD ≌四边形 A'B'C'D' .
【答案】(1)①②④
(2)解:选④CD = C'D',
证明:连接 AC 、 A'C',
在△ABC与△A'B'C'中,
,
∴△ABC ≌△A'B'C'(SAS ) ,
∴ AC=A'C',∠ACB=∠A'C'B', ∠BAC=∠B ' A 'C ',
∵∠BCD=∠B'C'D',
∴∠BCD - ∠ACB=∠B'C'D'- ∠A'C'B' ,
∴∠ACD=∠A'C'D',
在△ACD和△A'C'D 中,
,
∴△ACD ≌△A'C'D'(SAS ) ,
∴∠D=∠D ' , ∠DAC=∠D'A'C', DA=D'A',
∴∠BAC + ∠DAC=∠B'A'C' + ∠D'A'C' , 即∠BAD=∠B'A'D',
∴四边形 ABCD 和四边形 A'B'C'D' 中,
AB=A'B',BC=B'C' ,AD=A'D',DC=D'C',
∠B=∠B', ∠BCD=∠B'C'D' , ∠D=∠D' , ∠BAD=∠B'A'D',
∴四边形 ABCD ≌四边形 A'B'C'D' .
【完整解答】解:(1)符合要求的条件是①②④,
当选择① ∠A=∠A'时,
证明:连接 AC 、 A'C',
在△ABC 与△ A'B'C'中,
,
∴△ABC ≌△A'B'C'(SAS ) ,
∴ AC=A'C', ∠ACB=∠A'C'B',∠BAC=∠B ' A 'C ',
∵∠BCD=∠B'C'D' ,
∴∠BCD - ∠ACB=∠B'C'D' - ∠A'C'B',
∴∠ACD=∠A'C'D',
∵∠BAD=∠B'A'D',
∴∠BAD - ∠BAC=∠B'A'D'- ∠ B'A'C',
∴∠DAC=∠ D'A'C',
在△ACD 和△A'C'D 中,
,
∴△ACD ≌△A'C'D'(ASA ) ,
∴∠D=∠D ' , DC=D'C', DA=D'A' ,
∴四边形 ABCD 和四边形 A'B'C'D' 中,
AB=A'B',BC=B'C',AD=A'D',DC=D'C',
∠B=∠B', ∠BCD=∠B'C'D', ∠D=∠D' , ∠BAD=∠B'A'D',
∴四边形 ABCD ≌四边形 A'B'C'D';
当选择② ∠D=∠D'时,
证明:同理得到AC=A'C' ,∠ACD=∠A'C'D' ,
∵∠D=∠D',
在△ACD和△A'C'D 中,
,
∴△ACD ≌△A'C'D'(AAS ) ,
∴∠D=∠D ' , DC=D'C', DA=D'A',
∴四边形 ABCD 和四边形 A'B'C'D' 中,
AB=A'B' ,BC=B'C' ,AD=A'D' ,DC=D'C',
∠B=∠B' , ∠BCD=∠B'C'D' , ∠D=∠D' , ∠BAD=∠B'A'D' ,
∴四边形 ABCD ≌四边形 A'B'C'D';
当选择③ AD=A'D'时,
在△ACD 和△A'C'D 中,
AC=A'C' ,∠ACD=∠A'C'D',AD=A'D',
不符合全等的条件,不能得到△ACD ≌△A'C'D';
【思路引导】(1)连接AC、A′C′,根据全等三角形的判定和性质定理即可得到结论;(2)连接AC、A′C′,根据全等三角形的判定和性质定理即可得到结论.
苏科版八年级数学上册同步考点必刷练精编讲义必刷提高练【6.1函数】(原卷版+解析): 这是一份苏科版八年级数学上册同步考点必刷练精编讲义必刷提高练【6.1函数】(原卷版+解析),共27页。试卷主要包含了1 函数,03等内容,欢迎下载使用。
苏科版八年级数学上册同步考点必刷练精编讲义必刷提高练【3.2勾股定理的逆定理】(原卷版+解析): 这是一份苏科版八年级数学上册同步考点必刷练精编讲义必刷提高练【3.2勾股定理的逆定理】(原卷版+解析),共21页。试卷主要包含了2 勾股定理的逆定理,3,0,5,2,2,5﹣4﹣2等内容,欢迎下载使用。
苏科版八年级数学上册同步考点必刷练精编讲义必刷提高练【3.3勾股定理的应用】(原卷版+解析): 这是一份苏科版八年级数学上册同步考点必刷练精编讲义必刷提高练【3.3勾股定理的应用】(原卷版+解析),共29页。试卷主要包含了3 勾股定理的应用,5尺B.8尺C.8,5米B.1,5,等内容,欢迎下载使用。












