

苏科版八年级数学上册同步考点必刷练精编讲义必刷提高练【第2章《轴对称图形》章节达标检测】(原卷版+解析)
展开章节达标检测
考试时间:120分钟 试卷满分:100分
姓名:__________ 班级:__________考号:__________
一.选择题(共10小题,满分20分,每小题2分)
1.(2分)(2022春•雨花区校级期末)等腰三角形顶角度数比一个底角度数的2倍多20°,则这个底角的度数是( )
A.30°B.40°C.50°D.60°
2.(2分)(2021秋•望城区期末)在△ABC中,AB=AC,若∠B=84°,则∠A=( )
A.66°B.48°C.22°D.12°
3.(2分)(2021秋•长沙期末)如图,B在AC上,D在CE上,AD=BD=BC,∠ACE=25°,∠ADE的度数为( )
A.50°B.65°C.75°D.80°
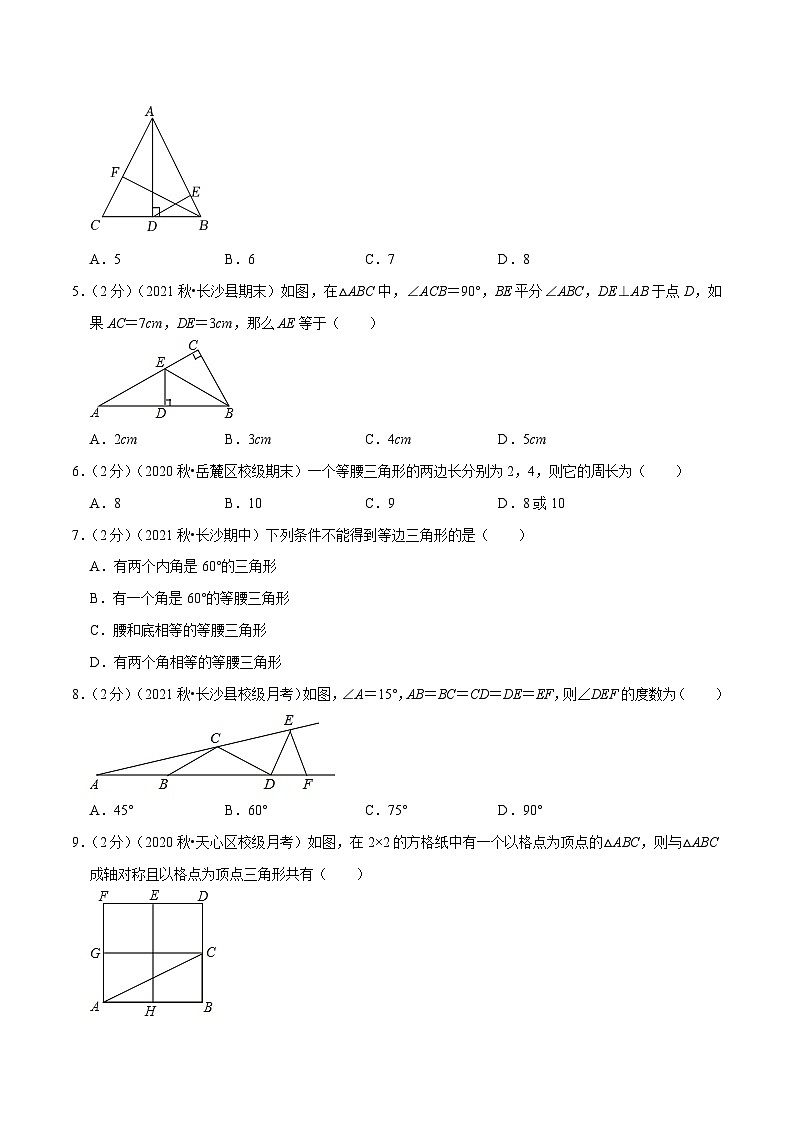
4.(2分)(2021秋•望城区期末)如图,△ABC中,AB=AC,AD⊥BC于点D,DE⊥AB于点E,BF⊥AC于点F,DE=4,则BF的长为( )
A.5B.6C.7D.8
5.(2分)(2021秋•长沙县期末)如图,在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于点D,如果AC=7cm,DE=3cm,那么AE等于( )
A.2cmB.3cmC.4cmD.5cm
6.(2分)(2020秋•岳麓区校级期末)一个等腰三角形的两边长分别为2,4,则它的周长为( )
A.8B.10C.9D.8或10
7.(2分)(2021秋•长沙期中)下列条件不能得到等边三角形的是( )
A.有两个内角是60°的三角形
B.有一个角是60°的等腰三角形
C.腰和底相等的等腰三角形
D.有两个角相等的等腰三角形
8.(2分)(2021秋•长沙县校级月考)如图,∠A=15°,AB=BC=CD=DE=EF,则∠DEF的度数为( )
A.45°B.60°C.75°D.90°
9.(2分)(2020秋•天心区校级月考)如图,在2×2的方格纸中有一个以格点为顶点的△ABC,则与△ABC成轴对称且以格点为顶点三角形共有( )
A.3个B.4个C.5个D.6个
10.(2分)(2020秋•雨花区校级月考)如图,∠AOB=120°,OP平分∠AOB,且OP=10.若点M,N分别在射线OA,OB上,且△PMN是边长为整数的等边三角形,则满足上述条件的点M有(参考数据:)( )
A.4个以上B.4个C.3个D.2个
二.填空题(共10小题,满分20分,每小题2分)
11.(2分)(2022春•长沙期中)如图,将长方形ABCD折叠,折痕为EF,BC的对应边B′C′与CD交于点M,若∠AEB′=30,则∠DFE的度数为 .
12.(2分)(2022•开福区三模)如图,在△ABC中,BC边的垂直平分线MN交AC边于点D,交BC边于点E,连接BD.若CE=4,△BDC的周长为18,求BD的长为 .
13.(2分)(2021秋•望城区期末)如图,△ABC和△ABE关于直线AB对称,△ABC和△ADC关于直线AC对称,CD与AE交于点F,若∠ABC=32°,∠ACB=18°,则∠CFE的度数为 .
14.(2分)(2021秋•长沙县期末)如图,∠AOB=60°,OC平分∠AOB,OC=6,点E是射线OA上的一个动点,那么EC的最小值为 .
15.(2分)(2022春•长沙期末)如图,在△ABC中,∠BAC=90°,AD是BC边上的高,E、F分别是AB、AC边的中点,若AB=8,AC=6,则△DEF的周长为 .
16.(2分)(2021秋•长沙期末)如图,△ABC的三条角平分线交于点O,O到AB的距离为3,且△ABC的周长为18,则△ABC的面积为 .
17.(2分)(2021春•岳麓区月考)如图,在四边形ABDE中,C是BD边的中点,BD=8,AB=2,DE=8.若∠ACE=135°,则线段AE长度的最大值为 .
18.(2分)(2018秋•天心区校级期中)如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M、N,再分别以点M、N为圆心,大于MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=3,AB=10,则△ABD的面积是 .
19.(2分)(2019秋•天心区校级月考)如图,已知等边三角形ABC的边长为3,过AB边上一点P作PE⊥AC于点E,Q为BC延长线上一点,取PA=CQ,连接PQ,交AC于M,则EM的长为 .
20.(2分)(2021•长沙模拟)如图,△ABC中,AD平分∠BAC,∠ACB=3∠B,CE⊥AD,AC=8,BC=BD,则CE= .
三.解答题(共9小题,满分60分)
21.(5分)(2021秋•望城区期末)如图,AB=AC,AC的垂直平分线交AB于D,交AC于E.
(1)若∠A=40°,求∠BCD的度数;
(2)若AE=5,△BCD的周长为17,求△ABC的周长.
22.(5分)(2021秋•开福区校级月考)小刚准备用一段长41米的篱笆围成三角形,用于养鸡,已知第一条边长m米,第二条边是第一条边的3倍少4米.
(1)请用含m的式子表示第三边的长度;
(2)若能围成一个等腰三角形,求这个三角形三边长.
23.(6分)(2020秋•开福区校级月考)如图,在△ABC中,AE是∠BAC的角平分线,交BC于点E,DE∥AB交AC于点D.
(1)求证AD=ED;
(2)若AC=AB,求证∠C=∠DEC;
(3)在(2)的条件下,若DE=3,求AC的长.
24.(6分)(2021秋•开福区校级期末)如图,在四边形ABCD中,BD所在的直线垂直平分线段AC,过点A作AF∥BC交CD于F,延长AB、DC交于点E.
(1)求证:AC平分∠EAF;
(2)求证:∠FAD=∠E;
(3)若∠EAD=90°,AE=5,AF=3,求CF的长.
25.(6分)(2019秋•岳麓区校级期中)如图,△ABC的外角∠DAC的平分线交BC边的垂直平分线于P点,PD⊥AB于D,PE⊥AC于E.
(1)求证:BD=CE;
(2)若AB=6cm,AC=10cm,求AD的长.
26.(8分)(2021秋•长沙期末)在△ABC中,点E,点F分别是边AC,AB上的点,且AE=AF,连接BE,CF交于点D,∠ABE=∠ACF.
(1)求证:△BCD是等腰三角形.
(2)若∠A=40°,BC=BD,求∠BEC的度数.
27.(8分)(2021秋•长沙期中)如图,△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB于E.
(1)若∠BAC=50°,求∠EDA的度数;
(2)求证:直线AD是线段CE的垂直平分线.
28.(8分)(2018秋•岳麓区校级月考)已知:如图,△ABC、△CDE都是等边三角形,AD、BE相交于点O,点M、N分别是线段AD、BE的中点.
(1)求证:AD=BE;
(2)求∠DOE的度数;
(3)求证:△MNC是等边三角形.
29.(8分)(2019•岳麓区校级开学)在△ABC中,AB=AC,CG⊥BA交BA的延长线于点G.一等腰直角三角尺按如图1所示的位置摆放,该三角尺的直角顶点为F,一条直角边与AC边在一条直线上,另一条直角边恰好经过点B.
(1)在图1中请你通过观察、测量BF与CG的长度,猜想并写出BF与CG满足的数量关系,然后证明你的猜想;
(2)当三角尺沿AC方向平移到图2所示的位置时,一条直角边仍与AC边在同一直线上,另一条直角边交BC边于点D,过点D作DE⊥BA于点E.此时请你通过观察、测量DE、DF与CG的长度,猜想并写出DE+DF与CG之间满足的数量关系,然后证明你的猜想;
(3)当三角尺在(2)的基础上沿AC方向继续平移到图3所示的位置(点F在线段AC上,且点F与点C不重合)时,(2)中的猜想是否仍然成立(不用说明理由).
题号
一
二
三
总分
评分
评卷人
得 分
评卷人
得 分
评卷人
得 分
2022-2023学年八年级数学上册考点必刷练精编讲义(苏科版)提高
第2章《轴对称图形》
章节达标检测
考试时间:120分钟 试卷满分:100分
一.选择题(共10小题,满分20分,每小题2分)
1.(2分)(2022春•雨花区校级期末)等腰三角形顶角度数比一个底角度数的2倍多20°,则这个底角的度数是( )
A.30°B.40°C.50°D.60°
解:设底角的度数是x°,则顶角的度数为(2x+20)°,
根据题意得:x+x+2x+20=180,
解得:x=40,
故选:B.
2.(2分)(2021秋•望城区期末)在△ABC中,AB=AC,若∠B=84°,则∠A=( )
A.66°B.48°C.22°D.12°
解:∵AB=AC,
∴∠B=∠C=84°,
∴∠A=180°﹣∠B﹣∠C=180°﹣84°﹣84°=12°,
故选:D.
3.(2分)(2021秋•长沙期末)如图,B在AC上,D在CE上,AD=BD=BC,∠ACE=25°,∠ADE的度数为( )
A.50°B.65°C.75°D.80°
解:∵BD=BC,∠ACE=25°,
∴∠BDC=∠C=25°,
∴∠ABD=50°,
∵AD=BD,
∴∠A=∠ABD=50°,
∴∠ADE=∠A+∠C=75°.
故选:C.
4.(2分)(2021秋•望城区期末)如图,△ABC中,AB=AC,AD⊥BC于点D,DE⊥AB于点E,BF⊥AC于点F,DE=4,则BF的长为( )
A.5B.6C.7D.8
解:∵△ABC中,AB=AC,AD⊥BC,
∴AD是△ABC的中线,
∴S△ABC=2S△ABD=2××DE•AB=DE•AB,
∵S△ABC=AC•BF,
∴AC•BF=DE•AB,
∵AC=AB,
∴BF=DE,
∵DE=4,
∴BF=8,
故选:D.
5.(2分)(2021秋•长沙县期末)如图,在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于点D,如果AC=7cm,DE=3cm,那么AE等于( )
A.2cmB.3cmC.4cmD.5cm
解:∵BE平分∠ABC,DE⊥AB,∠ACB=90°,
∴ED=EC,
∴AE=AC﹣EC=AC﹣ED=7﹣3=4(cm),
故选:C.
6.(2分)(2020秋•岳麓区校级期末)一个等腰三角形的两边长分别为2,4,则它的周长为( )
A.8B.10C.9D.8或10
解:①4是腰长时,三角形的三边分别为4、4、2,
4+2>4;
能组成三角形;
所以,周长为10;
②4是底边时,三角形的三边分别为2、2、4,
∵2+2=4,
∴不能组成三角形,
综上所述,周长为10.
故选:B.
7.(2分)(2021秋•长沙期中)下列条件不能得到等边三角形的是( )
A.有两个内角是60°的三角形
B.有一个角是60°的等腰三角形
C.腰和底相等的等腰三角形
D.有两个角相等的等腰三角形
解:A、有两个内角是60°的三角形是等边三角形,不符合题意;
B、有一个角是60°的等腰三角形是等边三角形,不符合题意;
C、腰和底相等的等腰三角形是等边三角形,不符合题意;
D、有两个角相等的等腰三角形可能不是等边三角形,符合题意;
故选:D.
8.(2分)(2021秋•长沙县校级月考)如图,∠A=15°,AB=BC=CD=DE=EF,则∠DEF的度数为( )
A.45°B.60°C.75°D.90°
解:∵AB=BC=CD=DE=EF,∠A=15°,
∴∠BCA=∠A=15°,
∴∠CBD=∠BDC=∠BCA+∠A=15°+15°=30°,
∴∠ECD=∠CED=∠A+∠CDB=45°
∴∠EDF=∠EFD=∠A+∠CED=60°
∴∠DEF=180°﹣(∠EDF+∠EFD)=180°﹣120°=60°.
故选:B.
9.(2分)(2020秋•天心区校级月考)如图,在2×2的方格纸中有一个以格点为顶点的△ABC,则与△ABC成轴对称且以格点为顶点三角形共有( )
A.3个B.4个C.5个D.6个
解:与△ABC成轴对称且以格点为顶点三角形有△ABG、△CDF、△AEF、△DBH,△BCG共5个,
故选:C.
10.(2分)(2020秋•雨花区校级月考)如图,∠AOB=120°,OP平分∠AOB,且OP=10.若点M,N分别在射线OA,OB上,且△PMN是边长为整数的等边三角形,则满足上述条件的点M有(参考数据:)( )
A.4个以上B.4个C.3个D.2个
解:在OB截取OK=OP,连接PK,则△OPK是等边三角形.
可以证明当∠MPN=60°时,△PMN是等边三角形.
理由:∵∠MPN=∠OPB=60°,
∴∠OPM=∠NPK,
∵OP=PK,∠POM=∠PKN,
∴△POM≌△PKN,
∴PM=PN,
∴△PMN是等边三角形,
当PM⊥OA时,PM的值最小,最小值为5,
PM的最大值为10,
∴5≤PM≤10,
∵PM是整数,
∴PM的值有两种可能,对应的点M有4种可能,
故选:B.
二.填空题(共10小题,满分20分,每小题2分)
11.(2分)(2022春•长沙期中)如图,将长方形ABCD折叠,折痕为EF,BC的对应边B′C′与CD交于点M,若∠AEB′=30,则∠DFE的度数为 75° .
解:由折叠可得,∠BEF=∠B'EF,
∵∠AEB′=30,∠AEB′+∠BEF+∠B'EF=180°,
∴∠BEF=×(180°﹣30°)=75°,
∵CD∥AB,
∴∠DFE=∠BEF=75°,
故答案为:75°.
12.(2分)(2022•开福区三模)如图,在△ABC中,BC边的垂直平分线MN交AC边于点D,交BC边于点E,连接BD.若CE=4,△BDC的周长为18,求BD的长为 5 .
解:∵MN垂直平分BC,CE=4,
∴BE=CE=4,BD=DC,
∵△BDC的周长为18,
∴BD+DC+BC=18,
∴2BD+BC=18,
∴2BD+4+4=18,
∴BD=5.
故答案为:5.
13.(2分)(2021秋•望城区期末)如图,△ABC和△ABE关于直线AB对称,△ABC和△ADC关于直线AC对称,CD与AE交于点F,若∠ABC=32°,∠ACB=18°,则∠CFE的度数为 118° .
解:∵△ABC和△ABE关于直线AB对称,△ABC和△ADC关于直线AC对称,
∴∠DCA=∠ACB=18°,∠BAC=∠BAE,
∵∠ABC=32°,
∴∠BAC=180°﹣18°﹣32°=130°=∠BAE,
∴∠EAC=360°﹣∠BAC﹣∠BAE=360°﹣130°﹣130°=100°,
∴∠CFE=∠ACD+∠EAC=18°+100°=118°,
故答案为:118°.
14.(2分)(2021秋•长沙县期末)如图,∠AOB=60°,OC平分∠AOB,OC=6,点E是射线OA上的一个动点,那么EC的最小值为 3 .
解:过点C作CE⊥OA于E,
根据垂线段最短可知,此时EC最小,
∵∠AOB=60°,OC平分∠AOB,
∴∠COE=30°,
∴CE=OC=×6=3,即EC的最小值为3,
故答案为:3.
15.(2分)(2022春•长沙期末)如图,在△ABC中,∠BAC=90°,AD是BC边上的高,E、F分别是AB、AC边的中点,若AB=8,AC=6,则△DEF的周长为 12 .
解:在Rt△ABC中,由勾股定理得:BC===10,
∵AD⊥BC,
∴∠ADB=∠ADC=90°,
∵E、F分别是AB、AC边的中点,AB=8,AC=6,BC=10,
∴DE=AB=4,DF=AC=3,EF=BC=5,
∴△DEF的周长=EF+DE+DF=5+4+3=12,
故答案为:12.
16.(2分)(2021秋•长沙期末)如图,△ABC的三条角平分线交于点O,O到AB的距离为3,且△ABC的周长为18,则△ABC的面积为 27 .
解:作OE⊥AB于E,OF⊥BC于F,OH⊥AC于H,
∵△ABC的三条角平分线交于点O,OE⊥AB,OF⊥BC,OH⊥AC,
∴OF=OH=OE=3,
∴△ABC的面积=×(AB+BC+AC)×3=27,
故答案为:27.
17.(2分)(2021春•岳麓区月考)如图,在四边形ABDE中,C是BD边的中点,BD=8,AB=2,DE=8.若∠ACE=135°,则线段AE长度的最大值为 10+4 .
解:作B关于AC的对称点F,D关于EC的对称点G,连接AF,FC,CG,EG,FG,如图所示:
∵C是BD边的中点,
∴CB=CD=BD,
由轴对称的性质可得△ACB≌△ACF,
∴CF=CB,
∴∠BCA=∠FCA.
同理可证:CD=CG,
∴∠DCE=∠GCE
∵CB=CD,
∴CG=CF
∵∠ACE=135°,
∴∠BCA+∠DCE=180°﹣135°=45°.
∴∠FCA+∠GCE=45°.
∴∠FCG=90°.
∴△FGC是等腰直角三角形.
∴FC=BD=4,
∴FG=FC=4,
∵AE=AB+4+DE.
∵AB=2,DE=8,
∴AE≤AF+FG+EG=10+4,
∴当A、F、G、E共线时AE的值最大,最大值为10+4,
故答案为:10+4.
18.(2分)(2018秋•天心区校级期中)如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M、N,再分别以点M、N为圆心,大于MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=3,AB=10,则△ABD的面积是 15 .
解:如图,作DE⊥AB于E,
由基本尺规作图可知,AD是△ABC的角平分线,
∵∠C=90°,DE⊥AB,
∴DE=DC=3,
∴△ABD的面积=×AB×DE=×10×3=15,
故答案为:15.
19.(2分)(2019秋•天心区校级月考)如图,已知等边三角形ABC的边长为3,过AB边上一点P作PE⊥AC于点E,Q为BC延长线上一点,取PA=CQ,连接PQ,交AC于M,则EM的长为 .
解:过P作PF∥BC交AC于F,如图所示:
∵PF∥BC,△ABC是等边三角形,
∴∠PFM=∠QCM,∠APF=∠B=60°,∠AFP=∠ACB=60°,∠A=60°,
∴△APF是等边三角形,
∴AP=PF=AF,
∵PE⊥AC,
∴AE=EF,
∵AP=PF,AP=CQ,
∴PF=CQ,
在△PFM和△QCM中,
,
∴△PFM≌△QCM(AAS),
∴FM=CM,
∵AE=EF,
∴EF+FM=AE+CM,
∴AE+CM=ME=AC,
∵AC=3,
∴ME=,
故答案为:.
20.(2分)(2021•长沙模拟)如图,△ABC中,AD平分∠BAC,∠ACB=3∠B,CE⊥AD,AC=8,BC=BD,则CE= .
解:延长CE交AB于F,过点D作DH⊥AB于H,DN⊥AC于N,过点A作AM⊥BC于M,如图所示:
∵CE⊥AD,
∴∠AEF=∠AEC=90°,
∵AD平分∠BAC,
∴∠FAE=∠CAE,DH=DN,
在△AEF与△AEC中,,
∴△AEF≌△AEC(ASA),
∴AF=AC=8,∠AFE=∠ACE,EF=CE,
∵∠AFC=∠B+∠ECD,
∴∠ACF=∠B+∠ECD,
∴∠ACB=2∠ECD+∠B,
∵∠ACB=3∠B,
∴2∠ECD+∠B=3∠B,
∴∠B=∠ECD,
∴CF=BF,
∵BC=BD,
∴=,
S△ADB=DH•AB=AM•BD,S△ACD=DN•AC=AM•CD,
∴=,
即==,
∴AB=AC=,
∴CF=BF=﹣8=,
∴CE=CF=,
故答案为:.
三.解答题(共9小题,满分60分)
21.(5分)(2021秋•望城区期末)如图,AB=AC,AC的垂直平分线交AB于D,交AC于E.
(1)若∠A=40°,求∠BCD的度数;
(2)若AE=5,△BCD的周长为17,求△ABC的周长.
解:(1)∵AB=AC
∴∠B=∠ACB=(180°﹣∠A)=70°,
∵MN垂直平分线AC
∴AD=CD,
∴∠ACD=∠A=40°,
∴∠BCD=∠ACB﹣∠ACD=70°﹣40°=30°;
(2)∵MN是AC的垂直平分线
∴AD=DC,AC=2AE=10,
∴AB=AC=10,
∵△BCD的周长=BC+CD+BD=AB+BC=17,
∴△ABC的周长=AB+BC+AC=17+10=27.
22.(5分)(2021秋•开福区校级月考)小刚准备用一段长41米的篱笆围成三角形,用于养鸡,已知第一条边长m米,第二条边是第一条边的3倍少4米.
(1)请用含m的式子表示第三边的长度;
(2)若能围成一个等腰三角形,求这个三角形三边长.
解:(1)第二条边的长为(3m﹣4)米,
第三边长为:41﹣m﹣(3m﹣4)=(45﹣4m)米;
(2)当m=3m﹣4时,解得m=2,三角形三边长分别为2,2,37,不符合三角形三边的关系,舍去;
当m=45﹣4m时,解得m=9,三角形三边长分别为9,9,23,不符合三角形三边的关系,舍去;
当3m﹣4=45﹣4m时,解得m=7,三角形三边长分别为7,7,17,符合三角形三边的关系;
综上所述,三角形三边长分别为7米,17米,17米.
23.(6分)(2020秋•开福区校级月考)如图,在△ABC中,AE是∠BAC的角平分线,交BC于点E,DE∥AB交AC于点D.
(1)求证AD=ED;
(2)若AC=AB,求证∠C=∠DEC;
(3)在(2)的条件下,若DE=3,求AC的长.
证明:(1)∵AE是∠BAC的角平分线,
∴∠DAE=∠BAE,
∵DE//AB,
∴∠DEA=∠EAB,
∴∠DAE=∠DEA,
∴AD=DE;
(2)解:∵AB=AC,AE是∠BAC的角平分线,
∴AE⊥BC,
∴∠C+∠CAE=90°,∠CED+∠DEA=90°,
∴∠C=∠DEC;
(3)由(2)得∠C=∠DEC,
∴DE=CD,
∵DE=3,
∴AD=DE=CD=3,
∴AC=6.
24.(6分)(2021秋•开福区校级期末)如图,在四边形ABCD中,BD所在的直线垂直平分线段AC,过点A作AF∥BC交CD于F,延长AB、DC交于点E.
(1)求证:AC平分∠EAF;
(2)求证:∠FAD=∠E;
(3)若∠EAD=90°,AE=5,AF=3,求CF的长.
(1)证明:∵BD所在的直线垂直平分线段AC,
∴BA=BC,
∴∠BAC=∠BCA,
∵BC∥AF,
∴∠CAF=∠BCA,
∴∠CAF=∠BAC,
即AC平分∠EAF;
(2)证明:∵BD所在的直线垂直平分线段AC,
∴DA=DC,
∴∠DAC=∠DCA,
∵∠DCA是△ACE的一个外角,
∴∠DCA=∠E+∠EAC,
∴∠E+∠EAC=∠FAD+∠CAF,
∵∠CAF=∠EAC,
∴∠FAD=∠E;
(3)解:∵∠EAD=90°,
∴∠E+∠ADE=90°,
由(2)知,∠FAD=∠E,
∴∠DAF+∠ADE=90°,
∴∠AFD=∠AFE=90°,
∵AE=5,AF=3,
∴EF==4,
设DF=x,
∵DE2﹣AE2=AD2=AF2+DF2,
∴(4+x)2﹣52=32+x2,
解得x=,
∴DF=,
∴DE=,
∴AD==,
∵BD所在的直线垂直平分线段AC,
∴AD=CD=,
∴CF=﹣=.
25.(6分)(2019秋•岳麓区校级期中)如图,△ABC的外角∠DAC的平分线交BC边的垂直平分线于P点,PD⊥AB于D,PE⊥AC于E.
(1)求证:BD=CE;
(2)若AB=6cm,AC=10cm,求AD的长.
(1)证明:连接BP、CP,
∵点P在BC的垂直平分线上,
∴BP=CP,
∵AP是∠DAC的平分线,
∴DP=EP,
在Rt△BDP和Rt△CEP中,,
∴Rt△BDP≌Rt△CEP(HL),
∴BD=CE;
(2)解:在Rt△ADP和Rt△AEP中,,
∴Rt△ADP≌Rt△AEP(HL),
∴AD=AE,
∵AB=6cm,AC=10cm,
∴6+AD=10﹣AE,
即6+AD=10﹣AD,
解得AD=2cm.
26.(8分)(2021秋•长沙期末)在△ABC中,点E,点F分别是边AC,AB上的点,且AE=AF,连接BE,CF交于点D,∠ABE=∠ACF.
(1)求证:△BCD是等腰三角形.
(2)若∠A=40°,BC=BD,求∠BEC的度数.
(1)证明:∵AE=AF,∠A=∠A,∠ABE=∠ACF,
∴△ABE≌△ACF(AAS),
∴AB=AC,∠ABE=∠ACF,
∴∠ABC=∠ACB,
∴∠ABC﹣∠ABE=∠ACB﹣∠ACF,
即∠DBC=∠DCB,
∴△BCD是等腰三角形;
(2)解:∵AB=AC,∠A=40°,
∴∠ABC=(180°﹣40°)=70°,
∵BD=BC,
∴∠BDC=∠BCD,
∵∠DBC=∠DCB,
∴△DBC是等边三角形,
∴∠DBC=60°,
∴∠ABE=10°,
∴∠BEC=∠A+∠ABE=50°.
27.(8分)(2021秋•长沙期中)如图,△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB于E.
(1)若∠BAC=50°,求∠EDA的度数;
(2)求证:直线AD是线段CE的垂直平分线.
(1)解:∵∠BAC=50°,AD平分∠BAC,
∴∠EAD=∠BAC=25°,
∵DE⊥AB,
∴∠AED=90°,
∴∠EDA=90°﹣25°=65°.
(2)证明:∵DE⊥AB,
∴∠AED=90°=∠ACB,
又∵AD平分∠BAC,
∴∠DAE=∠DAC,
∵AD=AD,
∴△AED≌△ACD,
∴AE=AC,
∵AD平分∠BAC,
∴AD⊥CE,AD平分线段EC,
即直线AD是线段CE的垂直平分线.
28.(8分)(2018秋•岳麓区校级月考)已知:如图,△ABC、△CDE都是等边三角形,AD、BE相交于点O,点M、N分别是线段AD、BE的中点.
(1)求证:AD=BE;
(2)求∠DOE的度数;
(3)求证:△MNC是等边三角形.
解:(1)∵△ABC、△CDE都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACB+∠BCD=∠DCE+∠BCD,
∴∠ACD=∠BCE,
在△ACD和△BCE中
,
∴△ACD≌△BCE,
∴AD=BE.
(2)解:∵△ACD≌△BCE,
∴∠ADC=∠BEC,
∵等边三角形DCE,
∴∠CED=∠CDE=60°,
∴∠ADE+∠BED=∠ADC+∠CDE+∠BED,
=∠ADC+60°+∠BED,
=∠CED+60°,
=60°+60°,
=120°,
∴∠DOE=180°﹣(∠ADE+∠BED)=60°,
答:∠DOE的度数是60°.
(3)证明:∵△ACD≌△BCE,
∴∠CAD=∠CBE,AD=BE,AC=BC
又∵点M、N分别是线段AD、BE的中点,
∴AM=AD,BN=BE,
∴AM=BN,
在△ACM和△BCN中
,
∴△ACM≌△BCN,
∴CM=CN,
∠ACM=∠BCN,
又∠ACB=60°,
∴∠ACM+∠MCB=60°,
∴∠BCN+∠MCB=60°,
∴∠MCN=60°,
∴△MNC是等边三角形.
29.(8分)(2019•岳麓区校级开学)在△ABC中,AB=AC,CG⊥BA交BA的延长线于点G.一等腰直角三角尺按如图1所示的位置摆放,该三角尺的直角顶点为F,一条直角边与AC边在一条直线上,另一条直角边恰好经过点B.
(1)在图1中请你通过观察、测量BF与CG的长度,猜想并写出BF与CG满足的数量关系,然后证明你的猜想;
(2)当三角尺沿AC方向平移到图2所示的位置时,一条直角边仍与AC边在同一直线上,另一条直角边交BC边于点D,过点D作DE⊥BA于点E.此时请你通过观察、测量DE、DF与CG的长度,猜想并写出DE+DF与CG之间满足的数量关系,然后证明你的猜想;
(3)当三角尺在(2)的基础上沿AC方向继续平移到图3所示的位置(点F在线段AC上,且点F与点C不重合)时,(2)中的猜想是否仍然成立(不用说明理由).
解:(1)BF=CG;
证明:在△ABF和△ACG中
∵∠F=∠G=90°,∠FAB=∠GAC,AB=AC
∴△ABF≌△ACG(AAS)
∴BF=CG;
(2)DE+DF=CG;
证明:过点D作DH⊥CG于点H(如图2)
∵DE⊥BA于点E,∠G=90°,DH⊥CG
∴四边形EDHG为矩形
∴DE=HG,DH∥BG
∴∠GBC=∠HDC
∵AB=AC
∴∠FCD=∠GBC=∠HDC
又∵∠F=∠DHC=90°,CD=DC
∴△FDC≌△HCD(AAS)
∴DF=CH
∴GH+CH=DE+DF=CG,即DE+DF=CG;
(3)仍然成立.
证明:过点D作DH⊥CG于点H(如图3)
∵DE⊥BA于点E,∠G=90°,DH⊥CG
∴四边形EDHG为矩形,
∴DE=HG,DH∥BG,
∴∠GBC=∠HDC,
∵AB=AC,
∴∠FCD=∠GBC=∠HDC,
又∵∠F=∠DHC=90°,CD=DC,
∴△FDC≌△HCD(AAS)
∴DF=CH,
∴GH+CH=DE+DF=CG,
即DE+DF=CG.
方法2.(2)
如图2,连接AD,
S△ABC=S△ABD+S△ACD=AB×DE+AC×DF=AB×DE+AB×DF=AB(DE+DF),
S△ABC=AB×CG,
∴AB×CG=AB(DE+DF),
即:DE+DF=CG.
(3)同(2)的方法得出,DE+DF=CG
苏科版八年级数学上册同步考点必刷练精编讲义必刷提高练【6.1函数】(原卷版+解析): 这是一份苏科版八年级数学上册同步考点必刷练精编讲义必刷提高练【6.1函数】(原卷版+解析),共27页。试卷主要包含了1 函数,03等内容,欢迎下载使用。
苏科版八年级数学上册同步考点必刷练精编讲义必刷提高练【第4章《实数》章节复习巩固】(原卷版+解析): 这是一份苏科版八年级数学上册同步考点必刷练精编讲义必刷提高练【第4章《实数》章节复习巩固】(原卷版+解析),共22页。试卷主要包含了下列四个命题中,正确的个数有等内容,欢迎下载使用。
苏科版八年级数学上册同步考点必刷练精编讲义必刷提高练【第3章《勾股定理》章节复习巩固】(原卷版+解析): 这是一份苏科版八年级数学上册同步考点必刷练精编讲义必刷提高练【第3章《勾股定理》章节复习巩固】(原卷版+解析),共38页。












