
苏科版八年级数学上册同步考点必刷练精编讲义必刷提高练【第5章《平面直角坐标系》章节复习巩固】(原卷版+解析)
展开考试时间:100分钟 试卷满分:100分
姓名:___________班级:___________考号:___________
一.选择题(共10小题,满分20分,每小题2分)
1.(2分)(2022秋•沙县期中)过点A(﹣2,6)和B(﹣2,8)作直线,则直线AB( )
A.与x轴平行B.与y轴平行
C.与y轴相交D.与x轴,y轴均相交
2.(2分)(2022秋•太原期中)在平面直角坐标系中,若点P(a,﹣5)与点Q(4,3)所在直线PQ∥y轴,则a的值等于( )
A.﹣5B.3C.﹣4D.4
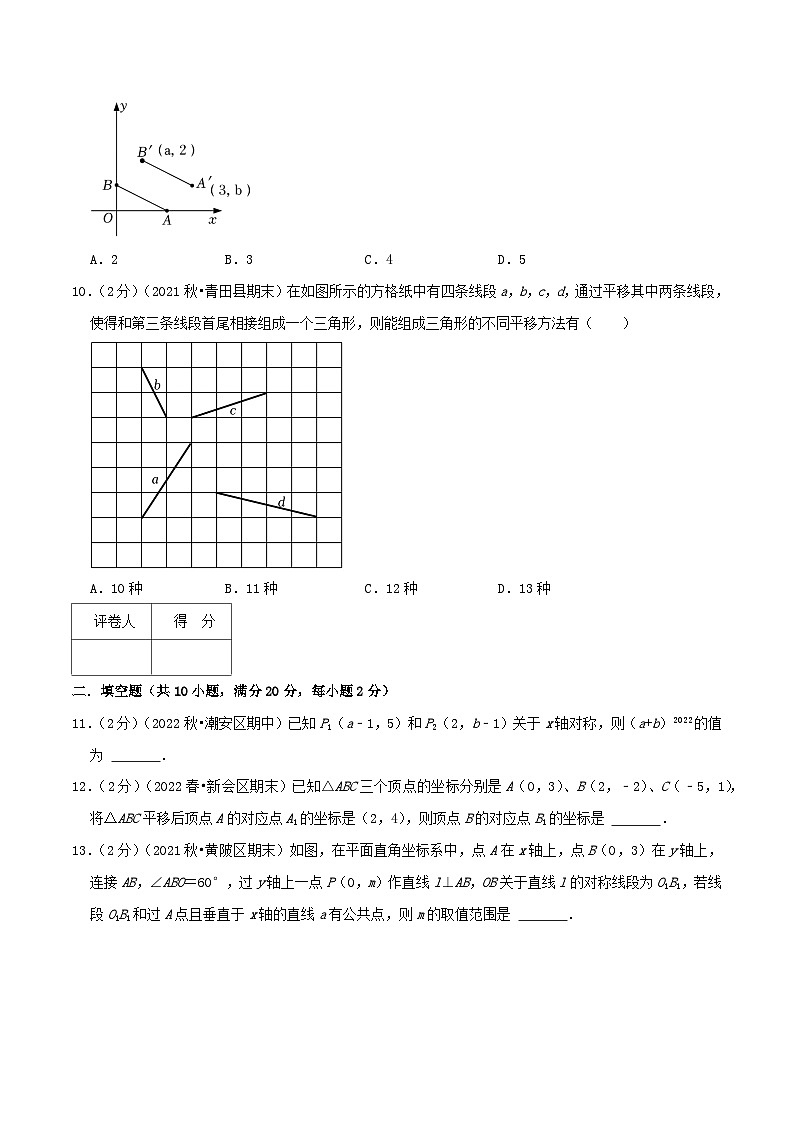
3.(2分)(2022秋•敦煌市期中)在平面直角坐标系中,下列各点在第三象限的是( )
A.(﹣1,2)B.(﹣3,﹣3)C.(1,4)D.(1,﹣3)
4.(2分)(2022秋•西安期中)如图是轰炸机机群的一个飞行队形,如果最后两架轰炸机的平面坐标分别为A(﹣2,1)和B(﹣2,﹣3),那么第一架轰炸机C的平面坐标是( )
A.(1,﹣2)B.(1,﹣1)C.(2,﹣1)D.(2,1)
5.(2分)(2022秋•天桥区期中)已知直线MN∥x轴,M点的坐标为(1,3),并且线段MN=4,则点N的坐标为( )
A.(5,3)B.(3,5)
C.(5,3)或(﹣3,3)D.(3,5)或(3,﹣3)
6.(2分)(2022春•思明区校级期中)把点A(﹣2,1)向上平移2个单位,再向左平移3个单位后得到B,点B的坐标是( )
A.(﹣5,3)B.(1,3)C.(1,﹣3)D.(﹣5,﹣1)
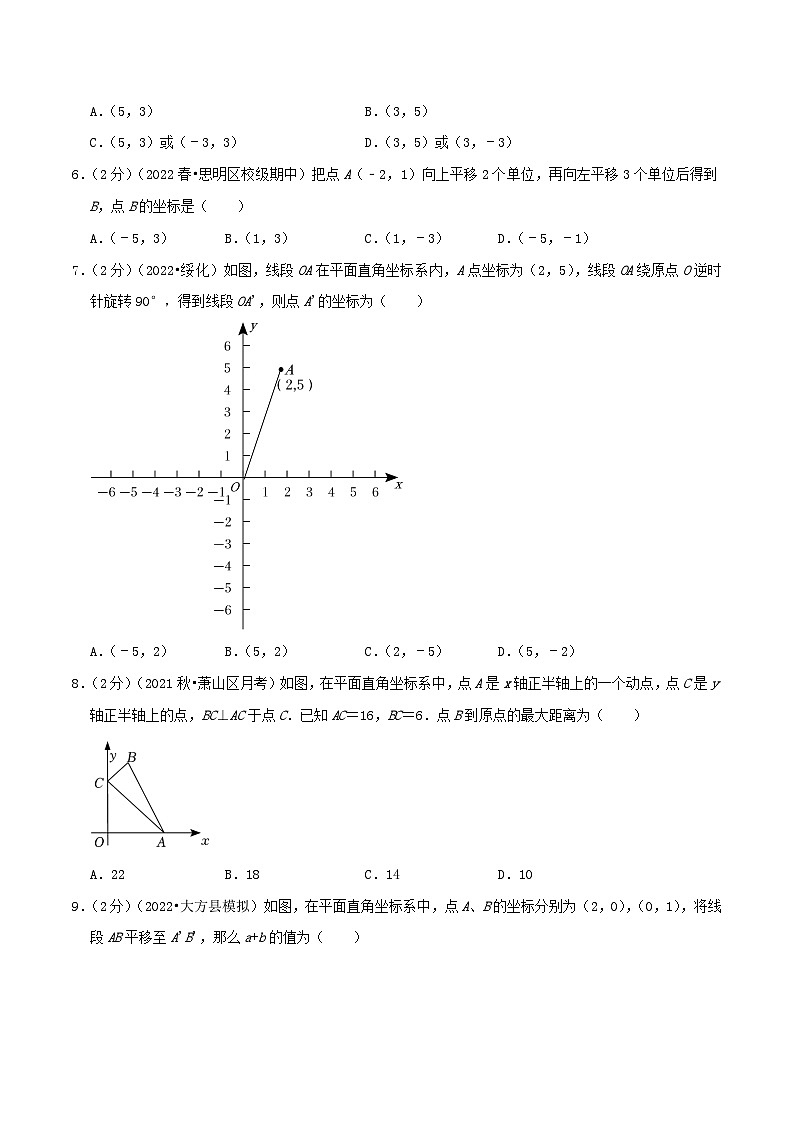
7.(2分)(2022•绥化)如图,线段OA在平面直角坐标系内,A点坐标为(2,5),线段OA绕原点O逆时针旋转90°,得到线段OA',则点A'的坐标为( )
A.(﹣5,2)B.(5,2)C.(2,﹣5)D.(5,﹣2)
8.(2分)(2021秋•萧山区月考)如图,在平面直角坐标系中,点A是x轴正半轴上的一个动点,点C是y轴正半轴上的点,BC⊥AC于点C.已知AC=16,BC=6.点B到原点的最大距离为( )
A.22B.18C.14D.10
9.(2分)(2022•大方县模拟)如图,在平面直角坐标系中,点A、B的坐标分别为(2,0),(0,1),将线段AB平移至A'B',那么a+b的值为( )
A.2B.3C.4D.5
10.(2分)(2021秋•青田县期末)在如图所示的方格纸中有四条线段a,b,c,d,通过平移其中两条线段,使得和第三条线段首尾相接组成一个三角形,则能组成三角形的不同平移方法有( )
A.10种B.11种C.12种D.13种
二.填空题(共10小题,满分20分,每小题2分)
11.(2分)(2022秋•潮安区期中)已知P1(a﹣1,5)和P2(2,b﹣1)关于x轴对称,则(a+b)2022的值为 .
12.(2分)(2022春•新会区期末)已知△ABC三个顶点的坐标分别是A(0,3)、B(2,﹣2)、C(﹣5,1),将△ABC平移后顶点A的对应点A1的坐标是(2,4),则顶点B的对应点B1的坐标是 .
13.(2分)(2021秋•黄陂区期末)如图,在平面直角坐标系中,点A在x轴上,点B(0,3)在y轴上,连接AB,∠ABO=60°,过y轴上一点P(0,m)作直线l⊥AB,OB关于直线l的对称线段为O1B1,若线段O1B1和过A点且垂直于x轴的直线a有公共点,则m的取值范围是 .
14.(2分)(2022•渭滨区一模)已知点A的坐标为(1,3),点B的坐标为(2,1),将线段AB沿某一方向平移后,点A的对应点的坐标为(﹣2,1),则点B对应点的坐标为 .
15.(2分)(2021秋•龙口市期末)如图,点A、B、C、D分别在正方形网格的格点上,其中A点的坐标为(﹣1,5),B点的坐标为(3,3),小明发现,线段AB与线段CD存在一种特殊关系,即其中一条线段绕着某点旋转一个角度可以得到另一条线段,则这个旋转中心的坐标是 .
16.(2分)(2021秋•柯桥区期末)定义:在平面直角坐标系中,把从点P出发沿横或纵方向到达点Q(至多拐一次弯)的路径长称为P,Q的“实际距离”.如图,若P(﹣1,1),Q(2,3),则P,Q的“实际距离”为5,即PS+SQ=5或PT+TQ=5.环保低碳的公共自行车,逐渐成为市民出行喜欢的交通工具.设A,B,C三个小区的坐标分别为A(3,3),B(6,﹣2),C(0,﹣4),若点M表示公共自行车停放点,且满足M到A,B,C的“实际距离”相等,则点M的坐标是 .
17.(2分)(2021秋•鄞州区期末)如图,在平面直角坐标系中,P是第一象限角平分线上的一点,且P点的横坐标为3.把一块三角板的直角顶点固定在点P处,将此三角板绕点P旋转,在旋转的过程中设一直角边与x轴交于点E,另一直角边与y轴交于点F,若△POE为等腰三角形,则点F的坐标为 .
18.(2分)(2021秋•汉阳区校级月考)如图,B(0,3),A为x轴上一动点,将线段AB绕点A顺时针旋转90°得AC,连接OC,则当OC取最小值时,A点的坐标是 .
19.(2分)(2021春•黄州区期末)如图,在平面直角坐标系中,A(4,0),B(﹣2,0),C(4,4),D(﹣2,6),点E在x轴上,满足∠BED=∠DEC,则点E的坐标为 .
20.(2分)(2020秋•双流区校级期中)已知如图,点A(﹣2,0)、B(4,0)、D(﹣5,9),设F为线段BD上一点(不含端点),连接AF,一动点M从点A出发,沿线段AF以每秒1个单位的速度运动到F,再沿线段FD以每秒个单位的速度运动到D后停止,当点F的坐标是 时,点M在整个运动过程中用时最少.
三.解答题(共8小题,满分60分)
21.(6分)(2022秋•邗江区校级期中)已知点Q(2m﹣6,m+2),试分别根据下列条件,求出m的值并写出点Q的坐标.
(1)若点Q在y轴上,求点Q的坐标.
(2)若点Q在∠xOy(即第一象限)角平分线上,求点Q的坐标.
22.(6分)(2022秋•淮北月考)在平面直角坐标系中,将线段AB平移得到的线段记为线段A′B′.
(1)如果点A,B,A′的坐标分别为A(﹣2,﹣1),B(1,﹣3),A′(2,3),直接写出点B′的坐标 ;
(2)已知点A,B,A',B'的坐标分别为A(m,n),B(2n,m),A′(3m,n),B′(6n,m),m和n之间满足怎样的数量关系?说明理由;
(3)已知点A,B,A′,B′的坐标分别为A(m,n+1),B(n﹣1,n﹣2),A′(2n﹣5,2m+3),B′(2m+3,n+3),求点A,B的坐标.
23.(6分)(2022春•惠东县期末)在平面直角坐标系中,三角形ABC经过平移得到三角形A'B'C',位置如图所示.
(1)分别写出点A,A′的坐标:A( , ),A′( , ).
(2)请说明三角形A′B'C′是由三角形ABC经过怎样的平移得到的;
(3)若点M(m,4﹣n)是三角形ABC内部一点,则平移后对应点M'的坐标为(2n﹣8,m﹣4),求m和n的值.
24.(6分)(2021秋•舞钢市期末)如图,在以点O为原点的平面直角坐标系中,点A、B的坐标分别为(a,0)、(a,b),点C在y轴上,且BC∥x轴,a、b满足|a﹣3|+=0.点P从原点出发,以每秒2个单位长度的速度沿着O﹣A﹣B﹣C﹣O的路线运动(回到点O为止).
(1)求出a、b的值并直接写出点A、B、C的坐标;
(2)当点P运动3秒时,连接PC、PO,求出点P的坐标,并直接写出∠CPO、∠BCP、∠AOP之间满足的数量关系.
25.(6分)(2022秋•龙岩期中)如图,平面直角坐标系xOy中,已知点A(0,3),点B(,0),连接AB则可量出∠OAB=30°.若对于平面内一点C,当△ABC是以AB为腰的等腰三角形时,称点C是线段AB的“等长点”.
(1)在点,点,点中,线段AB的“等长点”是点 ;
(2)若点D(m,n)是线段AB的“等长点”,且∠DAB=60°,求m和n的值.
26.(10分)(2022春•莒南县期末)如图,△DEF是△ABC经过某种变换得到的图形,点A与点D,点B与点E,点C与点F分别是对应点,观察点与点的坐标之间的关系,解答下列问题:
(1)分别写出点A与点D,点B与点E,点C与点F的坐标,并说说对应点的坐标有哪些特征;
(2)若点P(a+3,4﹣b)与点Q(2a,2b﹣3)也是通过上述变换得到的对应点,求a、b的值.
27.(10分)(2021秋•大埔县期末)在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(﹣4,5),(﹣1,3).
(1)请在如图所示的网格平面内作出平面直角坐标系;
(2)请作出△ABC关于y轴对称的△A′B′C′;
(3)写出点B′的坐标.
28.(10分)(2021秋•开福区校级期末)定义:对于平面直角坐标系中的任意两点A(x1,y1)和B(x2,y2),我们把它们的横、纵坐标的差的平方和的算术平方根称作这两点的“湘一根”,记作Q[A,B],即.
(1)若A(2,1)和B(﹣2,3),则Q[A,B]= ;
(2)若点M(1,2),N(a,a﹣3),其中a为任意实数,求Q[M,N]的最小值;
(3)若m为常数,且m>0,点A的坐标为(0,5m),B点的坐标为(8m,﹣m),C点的坐标为(x,0),求Q[A,C]+Q[B,C]的最小值以及Q[A,C]﹣Q[B,C]的最大值.(用含m的代数式表示)
题号
一
二
三
总分
得分
评卷人
得 分
评卷人
得 分
评卷人
得 分
2022-2023学年八年级数学上册考点必刷练精编讲义(苏科版)提高
第5章《平面直角坐标系》章节复习巩固
考试时间:100分钟 试卷满分:100分
一.选择题(共10小题,满分20分,每小题2分)
1.(2分)(2022秋•沙县期中)过点A(﹣2,6)和B(﹣2,8)作直线,则直线AB( )
A.与x轴平行B.与y轴平行
C.与y轴相交D.与x轴,y轴均相交
解:∵A(﹣2,6),B(﹣2,8),
∴直线AB为:x=﹣2,
∵直线x=﹣2与y轴平行,
∴AB∥y轴,
故选:B.
2.(2分)(2022秋•太原期中)在平面直角坐标系中,若点P(a,﹣5)与点Q(4,3)所在直线PQ∥y轴,则a的值等于( )
A.﹣5B.3C.﹣4D.4
解:∵直线PQ∥y轴,
∴P,Q横坐标相等,
∴a=4,
故选:D.
3.(2分)(2022秋•敦煌市期中)在平面直角坐标系中,下列各点在第三象限的是( )
A.(﹣1,2)B.(﹣3,﹣3)C.(1,4)D.(1,﹣3)
解:A、(﹣1,2)在第二象限,故此选项不符合题意;
B、(﹣3,﹣3)在第三象限,故此选项不符合题意;
C、(1,4)在第一象限,故此选项不符合题意;
D、(1,﹣3)在第四象限,故此选项不符合题意.
故选:B.
4.(2分)(2022秋•西安期中)如图是轰炸机机群的一个飞行队形,如果最后两架轰炸机的平面坐标分别为A(﹣2,1)和B(﹣2,﹣3),那么第一架轰炸机C的平面坐标是( )
A.(1,﹣2)B.(1,﹣1)C.(2,﹣1)D.(2,1)
解:根据题意可建立如图所示平面直角坐标系
由图可知轰炸机C的坐标是(2,﹣1),
故选:C.
5.(2分)(2022秋•天桥区期中)已知直线MN∥x轴,M点的坐标为(1,3),并且线段MN=4,则点N的坐标为( )
A.(5,3)B.(3,5)
C.(5,3)或(﹣3,3)D.(3,5)或(3,﹣3)
解:∵MN∥x轴,M点的坐标为(1,3),
∴N点的纵坐标为3,
而MN=4,
∴N点的横坐标为:1+4=5,或1﹣4=﹣3,
∴N点坐标为(﹣3,3)或(5,3).
故选:C.
6.(2分)(2022春•思明区校级期中)把点A(﹣2,1)向上平移2个单位,再向左平移3个单位后得到B,点B的坐标是( )
A.(﹣5,3)B.(1,3)C.(1,﹣3)D.(﹣5,﹣1)
解:∵A(﹣2,1)向上平移2个单位,再向左平移3个单位后得到B,
∴1+2=3,﹣2﹣3=﹣5;
点B的坐标是(﹣5,3).
故选:A.
7.(2分)(2022•绥化)如图,线段OA在平面直角坐标系内,A点坐标为(2,5),线段OA绕原点O逆时针旋转90°,得到线段OA',则点A'的坐标为( )
A.(﹣5,2)B.(5,2)C.(2,﹣5)D.(5,﹣2)
解:过点A作AB⊥x轴于点B,过点A′作A′C⊥x轴于点C,如图,
∵A点坐标为(2,5),
∴OB=2,AB=5.
由题意:∠AOA′=90°,OA=OA′.
∴∠AOB+∠A′OC=90°.
∵∠A′OC+∠A′=90°,
∴∠A′=∠AOB.
在△A′OC和△OAB中,
,
∴△A′OC≌△OAB(AAS).
∴A′C=OB=2,OC=AB=5,
∴A′(﹣5,2).
故选:A.
8.(2分)(2021秋•萧山区月考)如图,在平面直角坐标系中,点A是x轴正半轴上的一个动点,点C是y轴正半轴上的点,BC⊥AC于点C.已知AC=16,BC=6.点B到原点的最大距离为( )
A.22B.18C.14D.10
解:取AC的中点D,连接OD,BD,OB,如图,
∵D为AC的中点,∠AOC=90°,
∴OD=CD=AC=8.
∵∠ACB=90°,
∴BD===10.
当O,D,B三点不在一条直线上时,OB<OD+BD=8+10=18,
当O,D,B三点在一条直线上时,OB=OD+BD=8+10=18,
∴当O,D,B三点在一条直线上时,点B到原点的最大距离为18.
故选:B.
9.(2分)(2022•大方县模拟)如图,在平面直角坐标系中,点A、B的坐标分别为(2,0),(0,1),将线段AB平移至A'B',那么a+b的值为( )
A.2B.3C.4D.5
解:根据题意:A、B两点的坐标分别为A(2,0),B(0,1),A′的坐标为(3,b),B′(a,2),即线段AB向上平移1个单位,向右平移1个单位得到线段A′B′;
则:a=0+1=1,b=0+1=1,
a+b=2.
故选:A.
10.(2分)(2021秋•青田县期末)在如图所示的方格纸中有四条线段a,b,c,d,通过平移其中两条线段,使得和第三条线段首尾相接组成一个三角形,则能组成三角形的不同平移方法有( )
A.10种B.11种C.12种D.13种
解:如图,观察图象可知,线段b,c,d可以组成三角形,一共有5种情形,线段a,b,c可以组成三角形,一共有6种情形,共11种情形,
故选:B.
二.填空题(共10小题,满分20分,每小题2分)
11.(2分)(2022秋•潮安区期中)已知P1(a﹣1,5)和P2(2,b﹣1)关于x轴对称,则(a+b)2022的值为 1 .
解:∵P1(a﹣1,5)和P2(2,b﹣1)关于x轴对称,
∴a﹣1=2,b﹣1=﹣5,
解得a=3,b=﹣4,
则(a+b)2022=(3﹣4)2022=1.
故答案为:1.
12.(2分)(2022春•新会区期末)已知△ABC三个顶点的坐标分别是A(0,3)、B(2,﹣2)、C(﹣5,1),将△ABC平移后顶点A的对应点A1的坐标是(2,4),则顶点B的对应点B1的坐标是 (4,﹣1) .
解:∵△ABC三个顶点的坐标分别是A(0,3)、B(2,﹣2)、C(﹣5,1),将△ABC平移后顶点A的对应点A1的坐标是(2,4),
∴△ABC向右平移2个单位,向上平移一个单位得到△A1B1C1,
∴顶点B的对应点B1的坐标是(2+2,﹣2+1),即(4,﹣1),
故答案为:(4,﹣1).
13.(2分)(2021秋•黄陂区期末)如图,在平面直角坐标系中,点A在x轴上,点B(0,3)在y轴上,连接AB,∠ABO=60°,过y轴上一点P(0,m)作直线l⊥AB,OB关于直线l的对称线段为O1B1,若线段O1B1和过A点且垂直于x轴的直线a有公共点,则m的取值范围是 ﹣6≤m≤﹣3 .
解:如图1中,当点B1与A重合时,
∵直线l垂直平分线段AB,
∴PB=PA,
∵∠ABP=60°,
∴△APB是等边三角形,
∴PB=AB,
∵∠AOB=90°,∠ABO=60°,OB=3,
∴∠BAO=30°,
∴AB=2OB=6,
∴PB=AB=6,
∴OP=3,
∴m=﹣3,
如图2中,当点O1落在直线a上时,同法可证△OPO1是等边三角形,
∵AB∥OO1,OB∥AO1,
∴四边形ABOO1是平行四边形,
∴OO1=AB=6,
∴OP=OO1=6,
∴m=﹣6,
观察图象可知,满足条件的m的值为:﹣6≤m≤﹣3,
故答案为:﹣6≤m≤﹣3,
14.(2分)(2022•渭滨区一模)已知点A的坐标为(1,3),点B的坐标为(2,1),将线段AB沿某一方向平移后,点A的对应点的坐标为(﹣2,1),则点B对应点的坐标为 (﹣1,﹣1) .
解:∵A(1,3)的对应点的坐标为(﹣2,1),
∴平移规律为横坐标减3,纵坐标减2,
∴点B(2,1)的对应点的坐标为(﹣1,﹣1).
故答案为(﹣1,﹣1).
15.(2分)(2021秋•龙口市期末)如图,点A、B、C、D分别在正方形网格的格点上,其中A点的坐标为(﹣1,5),B点的坐标为(3,3),小明发现,线段AB与线段CD存在一种特殊关系,即其中一条线段绕着某点旋转一个角度可以得到另一条线段,则这个旋转中心的坐标是 (1,1)或(4,4). .
解:如图所示,分两种情形,旋转中心分别为(1,1)或(4,4);
故答案为(1,1)或(4,4).
16.(2分)(2021秋•柯桥区期末)定义:在平面直角坐标系中,把从点P出发沿横或纵方向到达点Q(至多拐一次弯)的路径长称为P,Q的“实际距离”.如图,若P(﹣1,1),Q(2,3),则P,Q的“实际距离”为5,即PS+SQ=5或PT+TQ=5.环保低碳的公共自行车,逐渐成为市民出行喜欢的交通工具.设A,B,C三个小区的坐标分别为A(3,3),B(6,﹣2),C(0,﹣4),若点M表示公共自行车停放点,且满足M到A,B,C的“实际距离”相等,则点M的坐标是 (2,﹣1) .
解:若设M(x,y),则由题目中对“实际距离”的定义可得方程组:|3﹣x|+|3﹣y|=y+2+6﹣x=x﹣0+y+4,
解得,x=2,y=﹣1,则M(2,﹣1)
故答案为:(2,﹣1).
17.(2分)(2021秋•鄞州区期末)如图,在平面直角坐标系中,P是第一象限角平分线上的一点,且P点的横坐标为3.把一块三角板的直角顶点固定在点P处,将此三角板绕点P旋转,在旋转的过程中设一直角边与x轴交于点E,另一直角边与y轴交于点F,若△POE为等腰三角形,则点F的坐标为 (0,0)或(0,3)或(0,6﹣3)或(0,6+3) .
解:△POE是等腰三角形的条件是:OP、PE、EO其中有两段相等,分情况讨论:
①当PE=OE时,PE⊥x轴,则PF⊥y轴,则OF=PE=3,故F的坐标是(0,3);
②当OP=PE时,∠OPE=90°=∠FPE,则F与O重合,即点F坐标为(0,0);
③当OP=OE,点E在x轴正半轴上时,过P作PA⊥x轴,PB⊥y轴,易得△PAE≌△PBF,
∴BF=AE=OE﹣AO=3﹣3,
此时,OF=3﹣(3﹣3)=6﹣3,
当点E在x轴负半轴上时,同理可得,BF=AE=OE+AO=3+3,
此时,OF=3+(3+3)=6+3,
∴点F的坐标是:(0,6﹣3)或(0,6+3).
故答案为:(0,0)或(0,3)或(0,6﹣3)或(0,6+3).
18.(2分)(2021秋•汉阳区校级月考)如图,B(0,3),A为x轴上一动点,将线段AB绕点A顺时针旋转90°得AC,连接OC,则当OC取最小值时,A点的坐标是 (﹣,0) .
解:如图,在x轴的正半轴上取一点H,使得OH=OB=3,在OB上取一点D,使得OD=OA.
∵OB=OH,OD=OA,
∴BD=AH,
∵∠HAC+∠OAB=90°,∠OAB+∠ABO=90°,
∴∠HAC=∠DBA,
∵BA=AC,
∵△BDA≌△AHC(SAS),
∴∠AHC=∠ADB,
∵OD=OA,∠AOD=90°,
∴∠ADO=45°,
∴∠AHC=∠ADB=135°,
∵H(3,0),
∴直线CH的解析式为y=x﹣3,
∴点C在直线y=x﹣3上运动,作OP⊥CH于P,OP=OH=,
此时P(,﹣),即C(,﹣),
设A(m,0),
∵AB=AC,
∴m2+32=(m﹣)2+()2,
解得m=﹣,
∴A(﹣,0).
故答案为(﹣,0).
19.(2分)(2021春•黄州区期末)如图,在平面直角坐标系中,A(4,0),B(﹣2,0),C(4,4),D(﹣2,6),点E在x轴上,满足∠BED=∠DEC,则点E的坐标为 (1,0)或(4,0) .
解:①如图,过D作DT⊥AC于T,
∵A (4,0),B (﹣2,0),C (4,4),D (﹣2,6),
∴∠DBA=∠BAT=∠ATD=90°,
BD=BA=6,
∴四边形ABDT是正方形,
连接AD,则∠BAD=∠TAD=45°,
∴E,A重合时,有∠BED=∠DEC,
∴E点的坐标为 (4,0).
②如图,过D作DH⊥EC 于H,
∵∠BED=∠DEC,DB⊥BE,
∴DB=DH=6,
∵C (4,4),D (﹣2,6),
∴CD=,
CH=,
由三角形内角和定理可得:∠BDE=∠HDE,
∵DB⊥BE,DH⊥EH,
∴BE=HE
设BE=x,
则HE=x,CE=x+2,AE=6﹣x,
∵CA⊥EA,CA=4,
∴(x+2)2=(6﹣x)2+42,
解得,x=3,
∴BE=3,
∴E点的坐标为(1,0);
综上,E点的坐标为(1,0)或(4,0).
故答案为:(1,0)或(4,0).
20.(2分)(2020秋•双流区校级期中)已知如图,点A(﹣2,0)、B(4,0)、D(﹣5,9),设F为线段BD上一点(不含端点),连接AF,一动点M从点A出发,沿线段AF以每秒1个单位的速度运动到F,再沿线段FD以每秒个单位的速度运动到D后停止,当点F的坐标是 (﹣2,6) 时,点M在整个运动过程中用时最少.
解:M在整个过程共用时:t==AF+DF,
如图分别作CD∥x轴,BC∥y轴,使直线CD、BC交于C,
∵D的坐标为(﹣5,9),B(4,0),
∴BC=|yD|=9,CD=|xB﹣xA|=|4+5|=9,
∴BC=CD,
∵∠BCD=90°,
∴△BCD为等腰直角三角形,
如上图过点F作EF⊥CD于点E,连接AE,
∴△DEF也是等腰直角三角形,
∴EF=DF,
∴t=AF+DF=AF+EF≥AE,
当AE⊥CD时,AE取得最小值,即AE=BC=9,
∴tmin=9,
此时,AE'与BD交于点F',
∴F'的横坐标等于A点的横坐标,
∴xF'=﹣2,
设直线BD的解析式为y=kx+b(k≠0),
将点B(4,0)和点D(﹣5,9)代入解析式得,
解得,
∴解析式为y=﹣x+4,
将x=﹣2代入y=﹣x+4,得y=6,
∴当F的坐标为(﹣2,6),点M在整个运动过程中用时最少,
故答案为:(﹣2,6).
三.解答题(共8小题,满分60分)
21.(6分)(2022秋•邗江区校级期中)已知点Q(2m﹣6,m+2),试分别根据下列条件,求出m的值并写出点Q的坐标.
(1)若点Q在y轴上,求点Q的坐标.
(2)若点Q在∠xOy(即第一象限)角平分线上,求点Q的坐标.
解:(1)点Q在y轴上,则2m﹣6=0,
解得m=3.
所以m+2=5,
故Q点的坐标是(0,5);
(2)当点Q在∠xOy(即第一象限)角平分线上,有2m﹣6=m+2,
解得m=8.
所以2m﹣6=10.
故Q点的坐标是(10,10).
22.(6分)(2022秋•淮北月考)在平面直角坐标系中,将线段AB平移得到的线段记为线段A′B′.
(1)如果点A,B,A′的坐标分别为A(﹣2,﹣1),B(1,﹣3),A′(2,3),直接写出点B′的坐标 (5,﹣1) ;
(2)已知点A,B,A',B'的坐标分别为A(m,n),B(2n,m),A′(3m,n),B′(6n,m),m和n之间满足怎样的数量关系?说明理由;
(3)已知点A,B,A′,B′的坐标分别为A(m,n+1),B(n﹣1,n﹣2),A′(2n﹣5,2m+3),B′(2m+3,n+3),求点A,B的坐标.
解:(1)∵A(﹣2,1)平移后得到点A′的坐标为(2,3),
∴向上平移了2个单位,向右平移了4个单位,
∴B(1,﹣3)的对应点B'的坐标为(1+4,﹣3+2),
即(5,﹣1).
故答案为:(5,﹣1);
(2)m=2n,
理由:∵将线段AB平移得到的线段记为线段A′B′,A(m,n),B(2n,m),A′(3m,n),B′(6n,m),
∴3m﹣m=6n﹣2n,
∴m=2n;
(3)∵将线段AB平移得到的线段记为线段A′B′,点A,B,A′,B′的坐标分别为A(m,n+1),B(n﹣1,n﹣2),A′(2n﹣5,2m+3),B′(2m+3,n+3),
∴2n﹣5﹣m=2m+3﹣(n﹣1),2m+3﹣(n+1)=(n+3)﹣(n﹣2),
解得m=6,n=9,
∴点A的坐标为(6,10),点B的坐标为(8,7).
23.(6分)(2022春•惠东县期末)在平面直角坐标系中,三角形ABC经过平移得到三角形A'B'C',位置如图所示.
(1)分别写出点A,A′的坐标:A( 1 , 0 ),A′( ﹣4 , 4 ).
(2)请说明三角形A′B'C′是由三角形ABC经过怎样的平移得到的;
(3)若点M(m,4﹣n)是三角形ABC内部一点,则平移后对应点M'的坐标为(2n﹣8,m﹣4),求m和n的值.
解:(1)观察图象可知A(1,0),A′(﹣4,4).
故答案为:1,0,﹣4,4;
(2)三角形A′B'C′是由三角形ABC向左平移5个单位,向上平移4个单位得到.
(3)由题意,,
解得,.
24.(6分)(2021秋•舞钢市期末)如图,在以点O为原点的平面直角坐标系中,点A、B的坐标分别为(a,0)、(a,b),点C在y轴上,且BC∥x轴,a、b满足|a﹣3|+=0.点P从原点出发,以每秒2个单位长度的速度沿着O﹣A﹣B﹣C﹣O的路线运动(回到点O为止).
(1)求出a、b的值并直接写出点A、B、C的坐标;
(2)当点P运动3秒时,连接PC、PO,求出点P的坐标,并直接写出∠CPO、∠BCP、∠AOP之间满足的数量关系.
解:(1)∵|a﹣3|+=0,
∴|a﹣3|=0,=0,
∴a=3,b=4,
∴A(3,0),B(3,4),C(0,4);
(2)如图,当P运动3秒时,点P运动了6个单位长度,
∵AO=3,
∴点P运动3秒时,点P在线段AB 上,且AP=3,
∴点P的坐标是(3,3);
如图,过点P作PE∥AO,
∵CB∥AO,PE∥AO,
∴CB∥PE,
∴∠BCP=∠EPC,∠AOP=∠EPO,
∴∠CPO=∠BCP+∠AOP.
25.(6分)(2022秋•龙岩期中)如图,平面直角坐标系xOy中,已知点A(0,3),点B(,0),连接AB则可量出∠OAB=30°.若对于平面内一点C,当△ABC是以AB为腰的等腰三角形时,称点C是线段AB的“等长点”.
(1)在点,点,点中,线段AB的“等长点”是点 C1,C2 ;
(2)若点D(m,n)是线段AB的“等长点”,且∠DAB=60°,求m和n的值.
解:(1)∵A(0,3),B( ,0),
∴AB=2 ,
∵点C1(0,3+2 ),
∴AC1=3+2﹣3=2,
∴AC1=AB,
∴C1是线段AB的“等长点”,
∵点C2(﹣,0),
∴AC2==2,
∴AC2=AB,
∴C2是线段AB的“等长点”,
∵点C3(0,﹣),
∴BC3=,
∴BC3≠AB,
∴C3不是线段AB的“等长点”;
故答案为:C1,C2;
(2)如图,
在Rt△AOB中,OA=3,OB=,
∴AB=2 ,tan∠OAB==,
∴∠OAB=30°,
当点D在y轴左侧时,
∵∠DAB=60°,
∴∠DAO=∠DAB﹣∠BAO=30°,
∵点D(m,n)是线段AB的“等长点”,
∴AD=AB,
∴D(﹣,0),
∴m=﹣,n=0,
当点D在y轴右侧时,
∵∠DAB=60°,
∴∠DAO=∠BAO+∠DAB=90°,
∴n=3,
∵点D(m,n)是线段AB的“等长点”,
∴AD=AB=2 ,
∴m=2,
综上,m=﹣,n=0或m=2,n=3.
26.(10分)(2022春•莒南县期末)如图,△DEF是△ABC经过某种变换得到的图形,点A与点D,点B与点E,点C与点F分别是对应点,观察点与点的坐标之间的关系,解答下列问题:
(1)分别写出点A与点D,点B与点E,点C与点F的坐标,并说说对应点的坐标有哪些特征;
(2)若点P(a+3,4﹣b)与点Q(2a,2b﹣3)也是通过上述变换得到的对应点,求a、b的值.
解:(1)由图象可知,点A(2,3),点D(﹣2,﹣3),点B(1,2),点E(﹣1,﹣2),点C(3,1),
点F(﹣3,﹣1);
对应点的坐标特征为:横坐标、纵坐标都互为相反数;
(2)由(1)可知,a+3+2a=0,4﹣b+2b﹣3=0,解得a=﹣1,b=﹣1.
27.(10分)(2021秋•大埔县期末)在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(﹣4,5),(﹣1,3).
(1)请在如图所示的网格平面内作出平面直角坐标系;
(2)请作出△ABC关于y轴对称的△A′B′C′;
(3)写出点B′的坐标.
解:(1)如图所示;
(2)如图所示;
(3)由图可知,B′(2,1).
28.(10分)(2021秋•开福区校级期末)定义:对于平面直角坐标系中的任意两点A(x1,y1)和B(x2,y2),我们把它们的横、纵坐标的差的平方和的算术平方根称作这两点的“湘一根”,记作Q[A,B],即.
(1)若A(2,1)和B(﹣2,3),则Q[A,B]= 2 ;
(2)若点M(1,2),N(a,a﹣3),其中a为任意实数,求Q[M,N]的最小值;
(3)若m为常数,且m>0,点A的坐标为(0,5m),B点的坐标为(8m,﹣m),C点的坐标为(x,0),求Q[A,C]+Q[B,C]的最小值以及Q[A,C]﹣Q[B,C]的最大值.(用含m的代数式表示)
解:(1)Q[A,B]==2,
故答案为:2.
(2)如图,由题意,点N在直线y=x﹣3上运动,
根据垂线段最短可知,当MN⊥直线y=x﹣3时,MN的值最小,此时N(3,0),
∵M(1,2),
∴Q[M,N]的最小值==2.
(3)如图1中,
∵m>0,A(0,5m),
∴B(8m,﹣m)在第四象限,A在y轴的正半轴上,
∴当A,C,B共线时,Q[A.C]+Q[C,B]的值最小,最小值==10m.
如图2中,作点B关于x轴的对称点B′,当点C在AB′的延长线上时,Q[A,C]﹣Q[B,C]的值最大,
最大值=Q[A,B′]==4m
苏科版八年级数学上册同步考点必刷练精编讲义必刷提高练【第6章《一次函数》章节复习巩固】(原卷版+解析): 这是一份苏科版八年级数学上册同步考点必刷练精编讲义必刷提高练【第6章《一次函数》章节复习巩固】(原卷版+解析),共33页。
苏科版八年级数学上册同步考点必刷练精编讲义必刷知识点【第5章《平面直角坐标系》章节复习巩固】(原卷版+解析): 这是一份苏科版八年级数学上册同步考点必刷练精编讲义必刷知识点【第5章《平面直角坐标系》章节复习巩固】(原卷版+解析),共6页。试卷主要包含了B的距离为AB=等内容,欢迎下载使用。
苏科版八年级数学上册同步考点必刷练精编讲义必刷基础练【第5章《平面直角坐标系》章节复习巩固】(原卷版+解析): 这是一份苏科版八年级数学上册同步考点必刷练精编讲义必刷基础练【第5章《平面直角坐标系》章节复习巩固】(原卷版+解析),共23页。












