人教数学九年级上册 23.1 第2课时 旋转作图 PPT课件

这是一份人教数学九年级上册 23.1 第2课时 旋转作图 PPT课件，共17页。

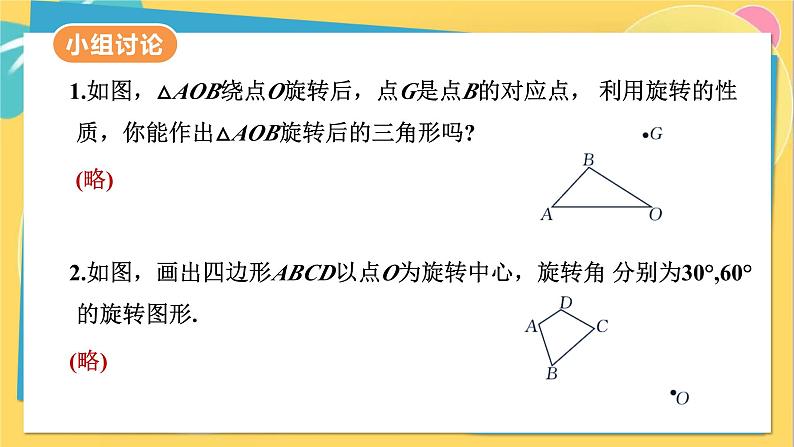
第2课时 旋转作图1.能根据旋转三要素与旋转性质作出简单平面图形旋转后的图形，进一步培养学生作图的能力.2.通过动手操作理解选择不同的旋转中心、不同的旋转角度，会出现不同的效果，培养学生的几何直观能力.3.经历对具有旋转特征的图形进行观察、分析、画图等过程，会用旋转图形的思想思考生活中的图形问题，体会将图形旋转作图转化为旋转关键点作图的化归思想.重点难点请同学们在硬纸板上挖一个三角形洞，再令挖一个小洞O 作为旋转中心，硬纸板下面放一张白纸，先在纸上描出挖掉的这个三角形的图案(△ABC)，然后围绕旋转中心转动硬纸板，再描出这个挖掉的三角形(△A'B'C')，观察这两个三角形.你能得到什么结论？这些图形有什么特点？它们是如何设计出来的呢？如果把钟表的指针看成四边形AOBC，如图，它绕点O旋转得到四边形DOEF.在这个过程中：（1）旋转中心是哪一点？（2）经过旋转，点A，B分别旋转到什么位置？（点A旋转到点D，点B旋转到点E）（3）图中有哪些相等的线段？（AO=DO,AC=DF,OB=OE,BC=EF）（4）∠AOD和∠BOE有什么数量关系？（点O）（∠AOD=∠BOE）自主探究1.请同学们阅读课本60页例题回答问题：①旋转中心是哪个点?②如何作出△ADE旋转后的图形?(在CB的延长线上取点E',使BE'=DE,连接AE',则△ABE'为旋转后的图形)③还有其他方法可以作出△ADE旋转后的图形吗?(答案不唯一，如：在CB的延长线上取点E',使∠AE'B=∠AED,则△ABE'为旋转后的图形)(点A)2.请同学们阅读课本61页并回答下列问题：①分别观察图23.1-7和图23.1-8中的两个旋转，你能得到什么?②请你通过改变旋转中心或旋转角设计出与图23.1-9中不同的图案自主探究(图23.1-7中的两个旋转，旋转中心不变，旋转角改变， 旋转效果不同；图23.1-8中的两个旋转，旋转角不变，旋 转中心改变，旋转效果不同)(答案不唯一，略)小组讨论1.如图，△AOB绕点O旋转后，点G是点B的对应点， 利用旋转的性质，你能作出△AOB旋转后的三角形吗? (略) 2.如图，画出四边形ABCD以点O为旋转中心，旋转角 分别为30°,60°的旋转图形.(略) 小组展示我提问我回答我补充我质疑提疑惑：你有什么疑惑？越展越优秀教师讲评知识点1:旋转作图（重点）对于同一个图案，如果选择的旋转中心、旋转角不同，会出现不同的旋转效果.旋转作图时，一定要先确定图形的“关键点”，将每个关键点绕“旋转中心”按规定的“方向”旋转一定的“角度”得到新的“关键点”，便可连成旋转后的图形.教师讲评知识点2:在平面直角坐标系中的图形旋转（难点）把点P (x, y) 绕原点分别顺时针旋转90°,180°,270°,360°,点P的对应点的坐标如下表所示：【题型一】旋转作图 例1: 如图，该图形围绕点O按下列角度旋转后，不能与其自身重合的是（ ）A.72° B.108° C.144° D.216°变式: 如图，五角星可以看成是一个三角形绕中心点(点O)旋转______次得到的，每次旋转的角度是__________.B四72°例 2 : 如题图，△ABC绕点C旋转后，顶点A的对应点为点D，试确定顶点B的对应点的位置，以及旋转后的三角形.【题型二】图形在平面直角坐标系中的旋转 例3: 如题图，在平面直角坐标系中，若将△ABC绕点C顺时针旋转90°，请在图中画出旋转后得到的△A1B1C，则点B的对应点B1的坐标为____________. （2，-1）（题图）解：如答图 . 变式： 如题图，△ABC的三个顶点都在格点上，且A（4,4），若将△ABC绕点O逆时针旋转180°，画出旋转后得到的△A1B1C1,则点A1的坐标为________，点B1的坐标为_________，点C1的坐标为________. （题图）解：如答图 . （-4，-4）（-1，-1）（-3，-1）本节课你收获了哪些？同学们，选择不同的旋转中心、旋转角，可以设计出不同的美丽图案，多动动你们灵活的小手，设计独一 无二的图案吧!（如何作出旋转后的图形）