数学八年级上册第十三章 轴对称13.3 等腰三角形13.3.1 等腰三角形课堂教学ppt课件

这是一份数学八年级上册第十三章 轴对称13.3 等腰三角形13.3.1 等腰三角形课堂教学ppt课件，共23页。PPT课件主要包含了旧知回顾，它是等腰三角形，都符合，三线合一等内容，欢迎下载使用。

1.通过剪纸、折纸等活动，进一步认识等腰三角形，了解等腰三角形是轴对称图形，培养学生的动手能力.2.通过学生自主探究、探索、猜想、验证等腰三角形的性质，并学会应用等腰三角形的性质，提高学生分析问题、解决问题的能力.3.结合等腰三角形性质的探索与证明过程，体会轴对称在研究几何问题中的作用，掌握转化和分类讨论的数学思想，发展学生的推理能力.
同学们，大家还记得什么是等腰三角形吗？等腰三角形中都有哪些元素呢？
（有两条边相等的三角形叫做等腰三角形.等腰三角形中，相等的两边叫做腰，第三边叫做底边，两腰的夹角叫做顶角，腰和底边的夹角叫做底角）
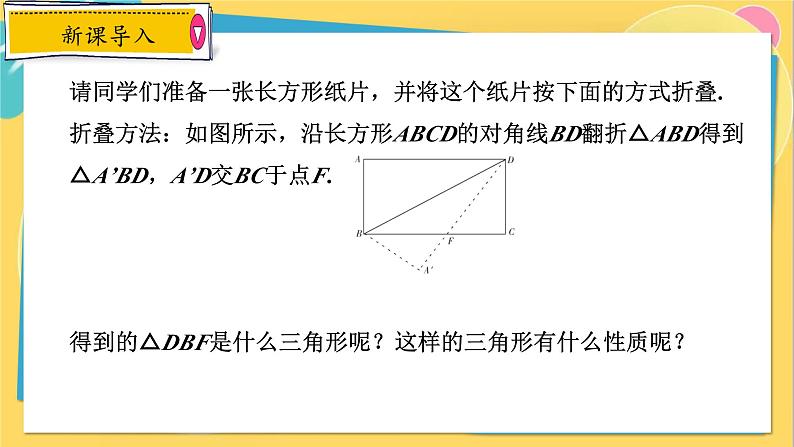
请同学们准备一张长方形纸片，并将这个纸片按下面的方式折叠.折叠方法：如图所示，沿长方形ABCD的对角线BD翻折△ABD得到△A’BD，A’D交BC于点F.得到的△DBF是什么三角形呢？这样的三角形有什么性质呢？
你从这几张图片中看到什么共同的几何图形？这些图形有哪些性质呢？
在我们学过的三角形中，有哪些轴对称图形呢？请你在纸上画出一个等腰三角形，你能找出它的对称轴吗？这个三角形有什么特殊性呢？
1.请同学们阅读课本 75 页上方的探究，按要求动手操作，观察你得到的三角形，它有什么特点？2.和同桌的比一比，你们得到的三角形都符合上述特点吗？
3.请同学们阅读课本75页下方的探究，动手操作并回答相应的问题.
（能.猜想：①等腰三角形的两个底角相等；②等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.仍然成立）
4.你能通过严格的逻辑推理证明猜想①吗？（1）请你写出已知、求证，画出图形.（2）结合你所画的图形，你认为证明等腰三角形两个底角相等的思路是什么？（3）如何在等腰三角形中构造出两个全等三角形呢？
（构造出两个全等三角形，利用全等三角形的性质得到对应角相等）
（作出底边上的中线或顶角平分线或底边上的高）
（4）请你完成证明过程.
5.我们证明了“等腰三角形的两个底角相等”，简写为“等边对等角”，请你用符号语言表示出来.
在△ABC中，AB＝AC，∴∠B＝∠C)
1.和小组同学交流一下你证明性质①的方法.2.请同学们讨论如何证明猜想②呢？分三种情况讨论，说明已知、求证及证明过程，并用符号语言表示3.通过证明得到等腰三角形的两个性质，请同学们分析一下：等腰三角形这两个性质定理成立的最根本原因是什么？
（等腰三角形是一个轴对称图形）
1.文字语言：等腰三角形的两个底角相等（简写成“等边对等角”）符号语言：在△ABC中，AB＝AC(已知)，∴∠B＝∠C(等边对等角)．
知识点．等腰三角形的性质（重难点）
2.文字语言：等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合（简写成“三线合一”）.符号语言：(1)∵AB＝AC，∠1＝∠2(已知)，∴BD＝CD，AD⊥BC(三线合一)．(2)∵AB＝AC，BD＝CD(已知)，∴∠1＝∠2，AD⊥BC(三线合一)．(3)∵AB＝AC，AD⊥BC(已知)，∴∠1＝∠2，BD＝CD(三线合一)
注：1.在①等腰；②底边上的高；③底边上的中线；④顶角平分线这四个元素中，①和②③④中的任意一个元素作为条件，就可以得到另外两个元素作为结论．2．等腰三角形是轴对称图形，对称轴为顶角平分线(或底边上的高或底边上的中线)所在的直线．
【题型一】等边对等角
例1：已知等腰三角形的底角为顶角的2倍，则这个等腰三角形的顶角的度数为___________.例2：如图，在△ABC中，D，E为AC上两点，连接BD，BE，若∠BED＝50°，∠BDE＝70°，AD＝BD，BE＝CE，则∠ABC＝________．
点拨：∵AD＝BD，∴∠A＝∠ABD.∵∠BDE＝∠A＋∠ABD＝70°，∴∠A＝35°.∵BE＝CE，∴∠C＝∠CBE.∵∠BED＝∠C＋∠CBE＝50°，∴∠C＝25°，∴∠ABC＝180°－∠A－∠C＝120°.
例3：如图，已知AB＝AC，DB＝DC，E是AD上一点，连接BE，CE.求证：∠ABE＝∠ACE.
证明：如图，连接BC，∵AB＝AC，DB＝DC，∴点A，D在线段BC的垂直平分线上．∴AD是线段BC的垂直平分线．∴EB＝EC.∴∠EBC＝∠ECB.∵AB＝AC，∴∠ABC＝∠ACB.∴∠ABC＋∠EBC＝∠ACB＋∠ECB，即∠ABE＝∠ACE.
【题型二】三线合一 例4：为了让枕木垂直于铁轨，工程人员的操作方法是：如图，从枕木DE上一点A往铁轨拉两条长度相等的固定绳AB与AC，当固定点B，C到点E的距离相等，且B，E，C在同一条直线上时，枕木DE就垂直于BC，工程人员这种操作方法的依据是________．
例5：如图，在△ABC中，AB＝AC，∠BAC的平分线交BC于点D，∠ABC的平分线交AD于点E，作EF⊥AB于点F，若EF＝3，则ED的长为________．
例6：如图，在△ABC中，AB＝AC，AD⊥BC，垂足为D，△ABC的周长为36，且AB：AD：BD＝13：12：5.求△ABC的面积．
请同学们回顾本节课所学的内容，你有哪些收获？
（1.等腰三角形的性质：①等边对等角；②三线合一.2.等腰三角形常用辅助线作法：作底边上的高、作底边上的中线、作顶角的平分线)