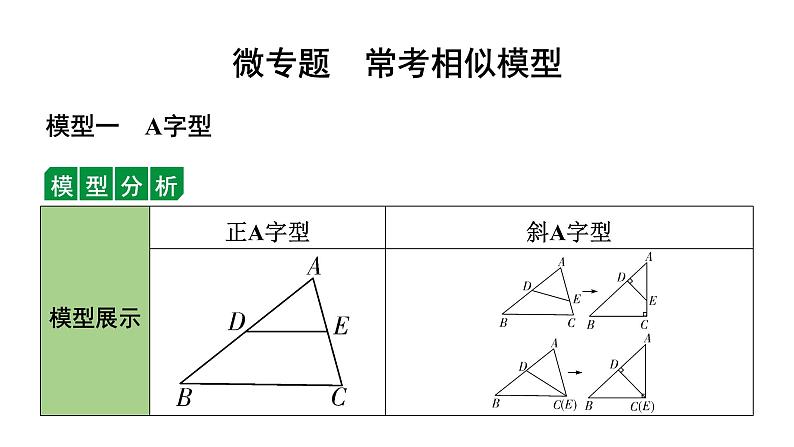

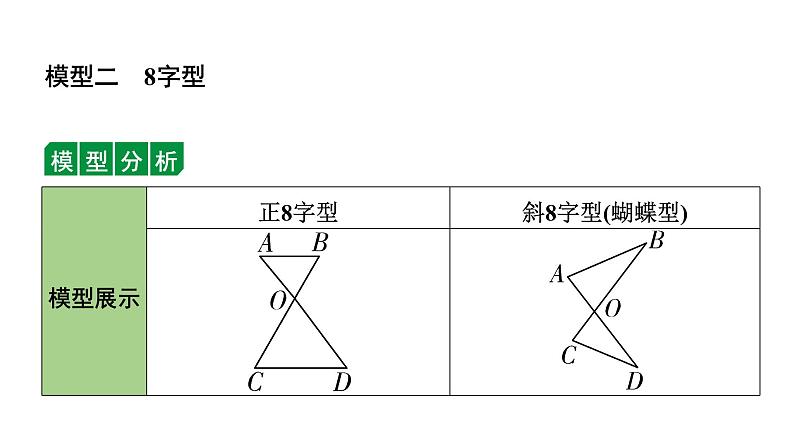

2024辽宁中考数学二轮专题复习 微专题 常考相似模型(课件)
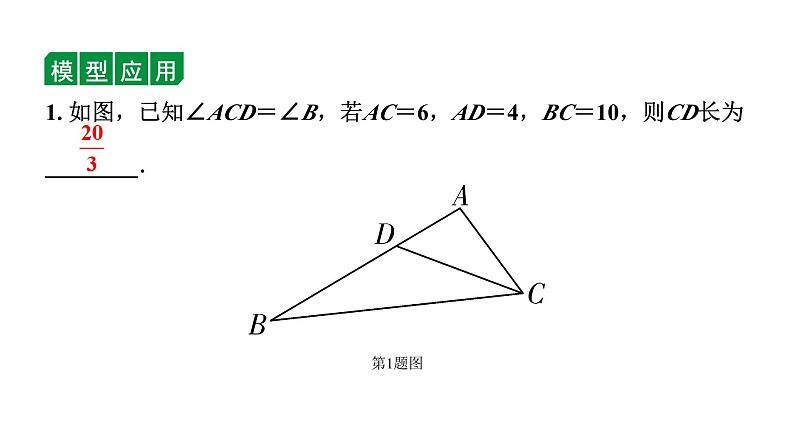
展开1. 如图,已知∠ACD=∠B,若AC=6,AD=4,BC=10,则CD长为________.
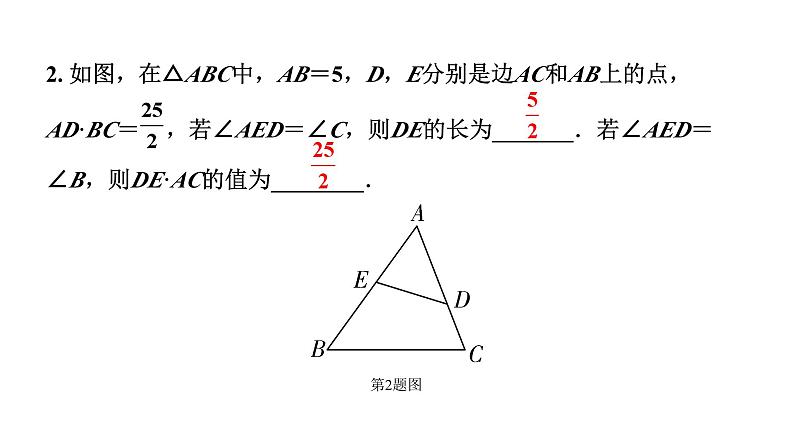
2. 如图,在△ABC中,AB=5,D,E分别是边AC和AB上的点,AD·BC= ,若∠AED=∠C,则DE的长为_______.若∠AED=∠B,则DE·AC的值为________.
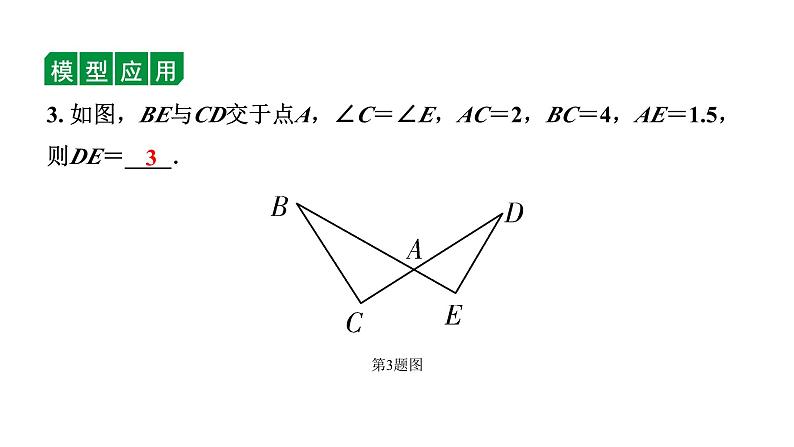
3. 如图,BE与CD交于点A,∠C=∠E,AC=2,BC=4,AE=1.5,则DE=____.
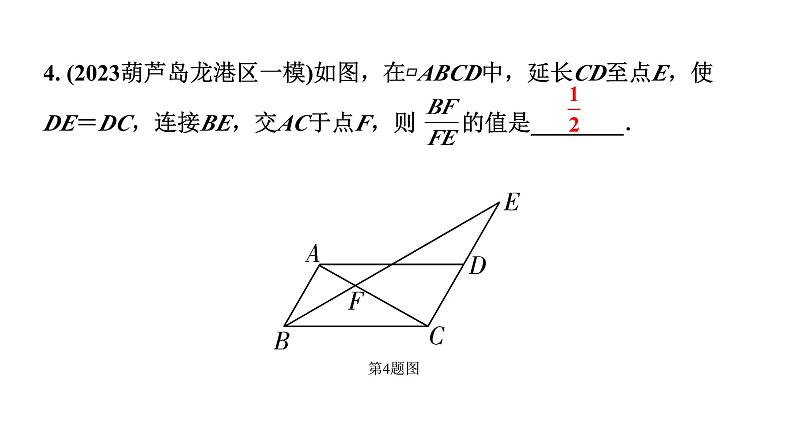
4. (2023葫芦岛龙港区一模)如图,在▱ABCD中,延长CD至点E,使DE=DC,连接BE,交AC于点F,则 的值是________.
5. 如图,△ABC是等腰直角三角形,∠C=90°,D为边BC上一点,连接AD,过点B作BE⊥AD,交AD的延长线于点E.若 ,则 的值为________.
6. 如图,在正方形ABCD中,AB=4,点E是DC延长线上的一点,连接BE,过点E作EF⊥BE交AD的延长线于点F.若CE=2,则DF的长为( ) A. 2 B. 3 C. 4 D. 6
8. 如图,在Rt△ABC中,∠ABC=90°,AB=6,BC=8,在Rt△MPN中,∠MPN=90°,点P在AC上,PM交AB于点E,PN交BC于点F,当PE=2PF时,AP=______.
9. 如图,已知△ABC是等边三角形,点D,E,F分别是AB,AC,BC边上的点,∠EDF=120°,设 =n.若 ,求n的值.
解:如解图,作DG∥BC交AC于点G,
∵△ABC是等边三角形,∴∠A=∠B=∠C=60°,∵DG∥BC,∴∠B=∠ADG=∠C=∠AGD=60°,∠BDG=120°,∴△ADG是等边三角形,∴AD=DG,
∵∠BGD=120°,∠EDF=120°,∴∠BDF+∠GDF=∠EDG+∠GDF=120°,∴∠BDF=∠GDE,∵∠B=∠AGD=60°,∴△DGE∽△DBF,∴ ,∴ ,
1. 如图,点O为平行四边形ABCD的对角线AC和BD的交点,点E为边BC的中点,连接AE交BD于点F,则 的值为________.
2. 如图,△ABC为锐角三角形,AD是BC边上的高,矩形PQMN的顶点P,N分别在AB,AC上,Q、M在BC上,若BC=12,AD=8,QM=x,矩形PQMN的面积是__________.(用含x的代数式表示)
3. 如图,在Rt△ABC中,∠ACB=90°,D为AC的中点,E为AB上一点,ED,BC的延长线交于点F,∠F=30°,ED=2,DF=6,BE= ,则BC的长为_______.
4. 如图,矩形ABCD中,AB=4,AD=6,点E是边CD上一点,EF⊥AE交BC于点F,则CF长的取值范围是____________.
5. 如图,在△ABC中,AB=2,AC= ,D为△ABC内部的一点,且CD⊥BD,在BD的延长线上取一点E,使得∠CAE=∠BAD.若∠ADE=∠ABC,且∠DBC=30°,则AD的长为________.
6. 如图,在Rt△ABC中,∠C=90°,AC=BC,AP、BP分别平分∠CAB、∠CBA,过点P作DE∥AB交AC于点D,交BC于点E.(1)求证:点P是线段DE的中点;
证明:(1)∵BP平分∠ABC,∴∠ABP=∠CBP,∵DE∥AB,∴∠ABP=∠EPB,∴∠CBP=∠EPB,∴BE=PE,同理可证DP=DA,
∵DE∥AB,∴ ,∵CA=CB,∴CE=CD,∴BE=AD,∴PE=PD,∴点P是DE的中点;
(2)求证:BP2=BE·BA.
7. 已知△ABC和△DCE中,AB=AC,DC=DE,BF=EF,点B,C,E都在同一直线上,且△ABC和△DCE在该直线同侧.(1)如图①,若∠BAC=∠CDE=90°,请猜想线段AF与DF之间的数量关系和位置关系,并证明你的猜想;
解:(1)猜想:AF=DF,AF⊥DF.
证明:如解图,过点A作AH⊥BC于点H,过点D作DJ⊥EC于点J.
∵AB=AC,DC=DE,∠BAC=∠CDE=90°,∴BH=CH,CJ=EJ,∴AH=BH=CH,DJ=CJ=EJ,∵BF=EF,∴HJ=BF=EF,∴BH=FJ=AH,FH=JE=DJ,∵∠AHF=∠FJD=90°,∴△AHF≌△FJD(SAS),∴AF=FD,∠HAF=∠JFD,
∵∠FAH+∠AFH=90°,∴∠AFH+∠DFJ=90°,∴∠AFD=90°,即AF⊥DF;
(2)如图②,若∠BAC=60°,∠CDE=120°,请直接写出线段AF与DF之间的数量关系和位置关系.
【解法提示】如解图②,过点A作AH⊥BC于点H,过点D作DJ⊥EC于点J.
2024辽宁中考数学二轮专题复习 微专题 常考全等模型(课件): 这是一份2024辽宁中考数学二轮专题复习 微专题 常考全等模型(课件),共47页。PPT课件主要包含了第1题图,模型二轴对称型,第2题图,第3题解图,模型三一线三等角型,锐角一线三等角,直角一线三垂直,钝角一线三等角,第4题图,第5题图等内容,欢迎下载使用。
2024海南中考数学二轮重点专题研究 微专题 四大常考相似模型(课件): 这是一份2024海南中考数学二轮重点专题研究 微专题 四大常考相似模型(课件),共33页。PPT课件主要包含了图①图②,第8题图等内容,欢迎下载使用。
2024北京中考数学二轮专题复习 微专题 三大常考相似模型(课件): 这是一份2024北京中考数学二轮专题复习 微专题 三大常考相似模型(课件),共18页。PPT课件主要包含了AD·AB,例1题图,∠ADE=∠ACB,△ADE∽△ACB,第1题图,第2题图,第3题图,模型二8字型,例2题图,△ABO∽△DCO等内容,欢迎下载使用。












