2024内蒙古中考数学二轮专题复习 二次函数与几何综合题 类型一 线段问题（课件）

这是一份2024内蒙古中考数学二轮专题复习 二次函数与几何综合题 类型一 线段问题（课件），共25页。PPT课件主要包含了满分技法，例1题图，t－t＋3，－10，－t2＋2t＋3，t－1，－t2＋3t，例2题图①，例2题图③等内容，欢迎下载使用。
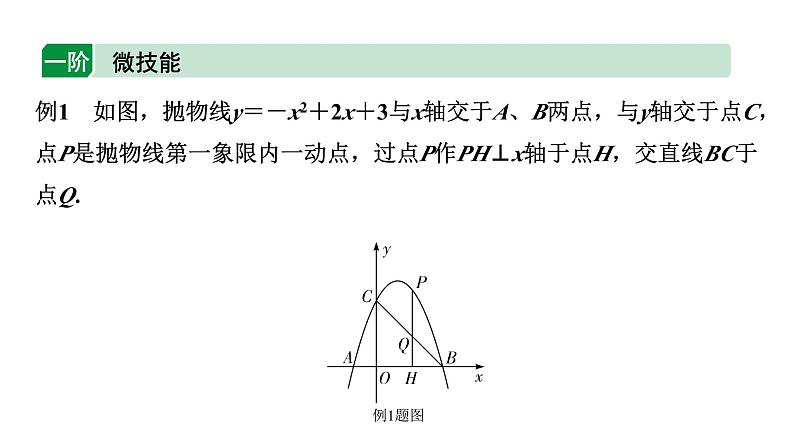
例1　如图，抛物线y＝－x2＋2x＋3与x轴交于A、B两点，与y轴交于点C，点P是抛物线第一象限内一动点，过点P作PH⊥x轴于点H，交直线BC于点Q.
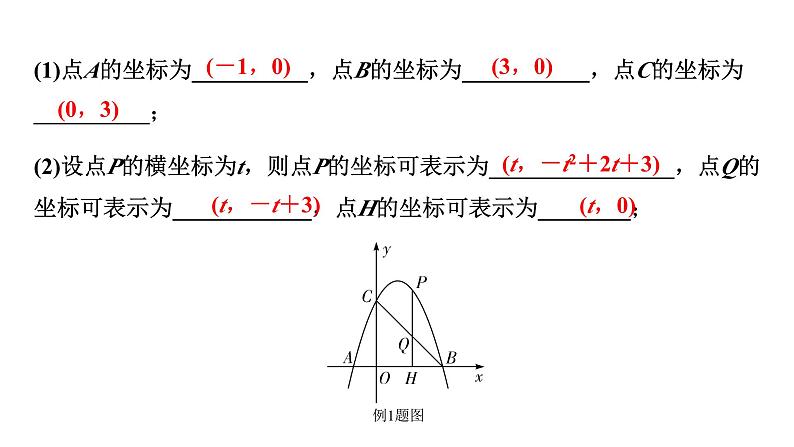
(2)设点P的横坐标为t，则点P的坐标可表示为________________，点Q的坐标可表示为____________，点H的坐标可表示为________；
(t，－t2＋2t＋3)
(1)点A的坐标为__________，点B的坐标为___________，点C的坐标为__________；
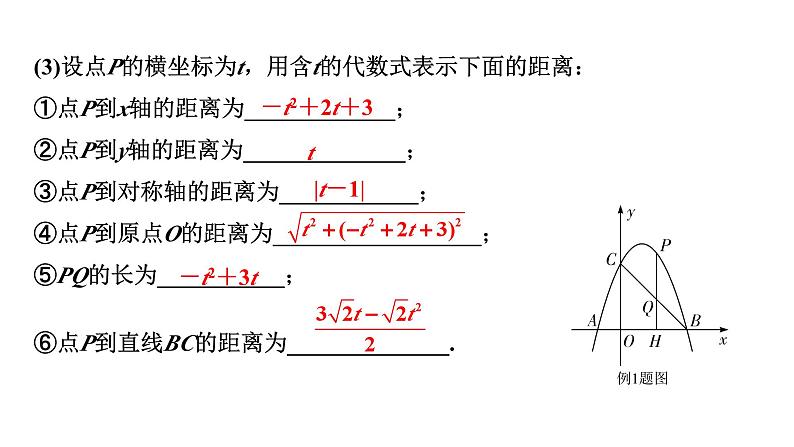
(3)设点P的横坐标为t，用含t的代数式表示下面的距离：①点P到x轴的距离为_____________；②点P到y轴的距离为______________；③点P到对称轴的距离为____________；④点P到原点O的距离为__________________；⑤PQ的长为___________； ⑥点P到直线BC的距离为______________.
1. 与x轴垂直的线段的长：纵坐标相减(上减下); 2. 与y轴垂直的线段的长：横坐标相减(右减左); 3. 斜线段时，可过线段端点分别作x轴、y轴垂线构造直角三角形，利用勾股定理、特殊三角函数值或相似进行求解．
例2　如图，已知二次函数y＝－ x2＋ x＋3的图象与x轴交于A、B两点(点B在点A右侧)，与y轴交于点C，对称轴为直线l，顶点为M，连接BC.
(1)若点P是抛物线在第一象限内一点，过点P作PQ∥y轴交线段BC于点Q，求线段PQ的最大值；
【思维教练】设出点P的横坐标，根据垂直于x轴的直线的坐标特征，表示出PQ的长度，利用二次函数性质求线段PQ的最大值．
解：(1)设点P的横坐标为p，则点P的坐标为(p，－ p2＋ p＋3)，∵PQ∥y轴，∴点Q的横坐标与点P相同．在函数y＝－ x2＋ x＋3中，令x＝0，得y＝3，∴C(0，3)．令y＝0，得－ x2＋ x＋3＝0，解得x＝－2或x＝4，∴A(－2，0)，B(4，0)，
设直线BC的解析式为y＝kx＋b，将B(4，0)，C(0，3)代入， 得 解得∴直线BC的解析式为y＝－ x＋3.∴点Q的坐标为(p，－ p＋3)，∴PQ＝－ p2＋ p＋3－(－ p＋3)＝－ p2＋ p＝－ (p－2)2＋
∵－ ＜0，0＜p＜4，∴当p＝2时，PQ有最大值，此时的最大值为 ；
(2)若点P是线段BC上方抛物线上一点，过点P作PH⊥BC于点H，求线段PH的最大值；
【思维教练】方法一：利用△PCB的面积求出线段PH的最大值；方法二：利用相似三角形求出线段PH的最大值．
∵－ ＜0，0＜p＜4，∴当p＝2时，S△PCB最大＝3.∵S△PCB＝ BC·PH，且BC＝ ＝5，∴ ×5×PH＝3，解得PH＝ ，∴线段PH的最大值为 ；
(3)若点P是对称轴l上一点，是否存在点P，使得PC＋PA最小，若存在，求出点P的坐标；若不存在，请说明理由；
【思维教练】将军饮马问题，将两定点同侧转化异侧问题，即可作点A关于对称轴l的对称点，恰好与点B重合，直线BC与对称轴l的交点即为要求的点P.
(3)存在．由(1)知A(－2，0)，B(4，0)，C(0，3)，∴抛物线的对称轴为直线x＝1，∴点A关于对称轴l的对称点的坐标为(4，0)，恰好与点B重合，
∴直线BC与对称轴的交点即为使得PC＋PA最小时点P的位置．由(1)知，直线BC的解析式为y＝－ x＋3，∴当x＝1时，y＝ ， ∴点P的坐标为(1， )；
(4)要使△BMP的周长最小，由于BM为定值，即使PM＋PB最小即可．如解图，作点M关于y轴的对称点M′，连接BM′交y轴与点P，此时点P满足△BMP的周长最小．
(4)若点P是y轴上一点，当以B、M、P为顶点的三角形周长最小时，求点P的坐标；
【思维教练】将军饮马问题，当△BMP的周长最小时，由于BM是定值，即求PM＋BM的最小值.
二次函数解析式可化为y＝－ (x－1)2＋ ，∴M(1， )， ∴M′(－1， )． ∵B(4，0)，∴设直线BM′的解析式为y＝kx＋b，将M′(－1， )，B(4，0)代入，
得 解得 ∴直线BM′的解析式为y＝－ x＋ ，当x＝0时，y＝ ，∴此时点P的坐标为(0， )．
(5)对称轴l上是否存在点P，使点P到直线BC的距离等于点P到点A的距离？若存在，求出点P的坐标；若不存在，请说明理由．
【思维教练】用(2)中的方法表示出点P到直线BC的长，再用勾股定理表示出PA的长，列关系式求解.
由(4)知，M(1， )，∴当x＝1时，y＝－ x＋3＝ ，∴E(1， )．由(1)知，A(－2，0)，B(4，0)，C(0，3)，∴CO＝3，BO＝4，∴BC＝5.在Rt△COB中，sin∠OCB＝ ，
∴sin∠PEQ＝设点P的坐标为(1，t)， ∴ ，解得PQ＝ ∵点P到直线BC的距离等于点P到点A的距离，∴PQ＝PA， ∴ ，解得t＝－4. ∴点P的坐标为(1，－4)．
已知：抛物线y＝ax2＋bx＋c经过A(－1，0)，B(3，0)，C(0，3)三点．(1)求抛物线的解析式；
(2)如图①，点P为直线BC上方抛物线上任意一点，连接PC、PB、PO，PO交直线BC于点E，设 ＝k，求当k取最大值时点P的坐标，并求此时k的值；
(2)如解图，过点P作PF∥y轴交BC于点F，
设点P的坐标为(x，－x2＋2x＋3)，则点F的坐标为(x，－x＋3)，∵PF∥y轴，∴△PFE∽△OCE， ∴ ∴ ∵－1＜0，∴当x＝ 时，k取得最大值 ，此时点P的坐标为( ， )；
(3)如图②，点Q为抛物线对称轴与x轴的交点，点C关于x轴的对称点为点D.求△BDQ的周长及tan∠BDQ的值．
∵B(3，0)，∴OB＝OD＝3.∵∠BOD＝90°，∴DQ＝ ，BD＝ OB＝∴△BDQ的周长＝BQ＋DQ＋BD＝2＋ ＋3 .在Rt△OBD中，∵∠BOD＝90°，OB＝OD，∴∠DBO＝∠BDO＝45°.∵∠BTQ＝90°，∴△BQT是等腰直角三角形，