2024内蒙古中考数学一轮知识点复习 第8课时 分式方程及其应用（课件）

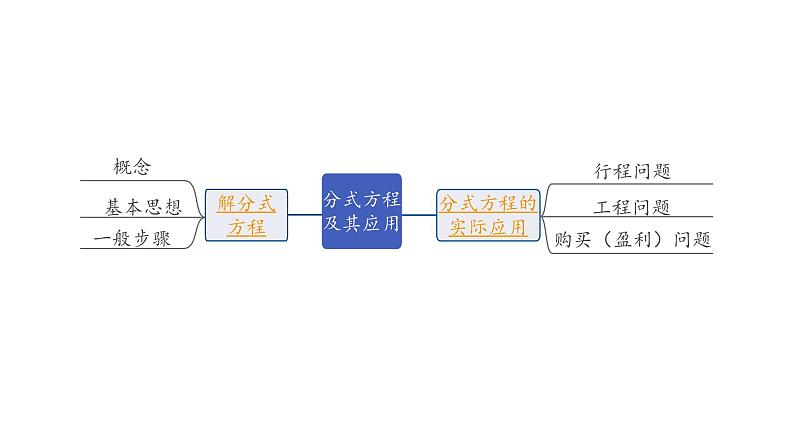
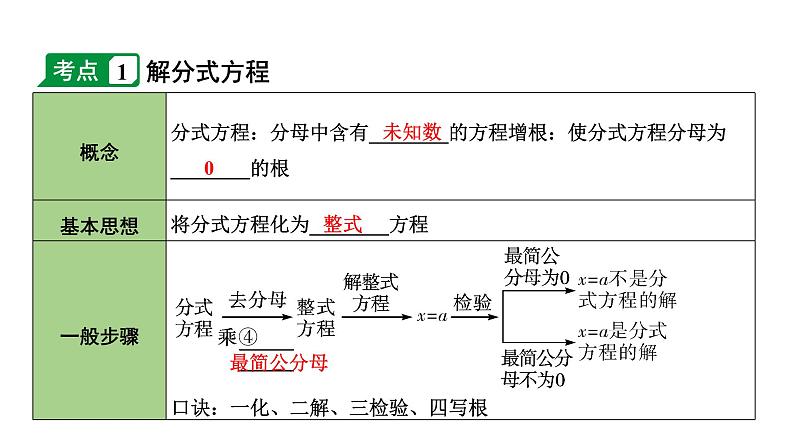
这是一份2024内蒙古中考数学一轮知识点复习 第8课时 分式方程及其应用（课件），共32页。PPT课件主要包含了分式方程及其应用，考点精讲，解分式方程，未知数，最简公分母，分式方程的实际应用，6－2x，－2x，－4x，x＋8等内容，欢迎下载使用。
【对接教材】北师：八下第五章P125～P130；　　人教：八上第十五章P149～P155.
例1　解方程： － ＝2.解：x＋2＝①___________，(去分母，方程两边同乘②__________)x＋2＝③______________，(去括号)5x＝④____________，(移项、合并同类项)x＝⑤____________，(系数化为1，方程两边同除以⑥_______)检验：⑦______________________________，∴x＝⑧______是原分式方程的解．
当x＝2时，6－2x＝2≠0
解分式方程时，需注意以下三点：1．最简公分母与分母互为相反数时注意符号；2．常数项或整式部分也要乘最简公分母；3．注意检验，检验解出的根是否会使最简公分母为零．
例2 某校为了落实让中华传统体育在校园绽放光彩，计划在课余时间开设象棋班和围棋班．(1)现需购买一批数量相同的象棋和围棋供兴趣班使用①，其中购买象棋用了350元②，购买围棋用了630元③，若每副围棋比每副象棋贵8元④，求每副围棋和象棋各是多少元？
【分层分析】设每副象棋x元，则根据题干④可得每副围棋______元，根据题干②可得购买象棋的数量为________，根据题干③可得购买围棋的数量为________，根据题干①可列等量关系式为____________．
解：(1)设每副象棋x元，则每副围棋(x＋8)元，由题意，得 ，解得x＝10，经检验，x＝10是原分式方程的解，且符合题意，∴x＋8＝18(元)，答：每副象棋10元，每副围棋18元；
(2)由于学生积极参与，全校有150人报名参加围棋班⑤，120人报名参加象棋班⑥，学校计划平均分成若干个小组，已知围棋班一个小组的人数比象棋班一个小组的人数多50%⑦，结果围棋班比象棋班少5组⑧，求围棋班一个小组的人数．
【分层分析】设象棋班一个小组的人数为x人，则根据题干⑦可得围棋班一个小组的人数为____人，根据题干⑤可得围棋班小组的数量为________，根据题干⑥可得象棋班小组的数量为___________，根据题干⑧可列等量关系式为_______________________________．
解：(2)设象棋班一个小组的人数为x人，则围棋班一个小组的人数为1.5x人，由题意，得 ＝5，解得x＝4，经检验，x＝4是原分式方程的解，且符合题意，∴1.5x＝6(人)，答：围棋班一个小组的人数为6人；
(3)为了提高围棋水平，小明和邻居小刚两人相约周末去市少年宫学习围棋，已知小明家与市少年宫的距离为4800米⑨，出发时，由于小明临时有事，小刚骑自行车先走，10分钟后小明乘公交车出发，结果小明比小刚提前5分钟到达⑩，已知公交车的平均速度是骑自行车平均速度的2倍⑪，求小刚的平均速度．
【分层分析】设小刚的平均速度为x米/分钟，则根据题干⑪可得小明的平均速度为________米/分钟，根据题干⑨可得小刚到达少年宫所用的时间为________，小明到达少年宫所用的时间为________，根据题干⑩可列等量关系式为_____________________________．
解：(3)设小刚的平均速度为x米/分钟，则小明的平均速度为2x米/分钟，由题意，得 ，解得x＝160，经检验，x＝160是原分式方程的解，且符合题意，答：小刚的平均速度为160米/分钟．
1. (2023包头14题3分)分式方程 ＋ ＝1的解是________．2. (2022呼和浩特13题3分)分式 与 的最简公分母是________，方程 － ＝1的解是_________．
3．解分式方程： － ＝0.
解：方程两边同乘(x－1)(x＋1)，得3x＋3－x－3＝0，解得x＝0，检验：当x＝0时，(x－1)(x＋1)＝－1≠0，∴x＝0是原分式方程的解．
4．(2023广西北部湾经济区)解分式方程： ＝ ＋1.
解：方程两边同乘以(3x＋3)，得3x＝x＋3x＋3，解得x＝－3，检验：当x＝－3时，3x＋3＝－6≠0，∴x＝－3是原分式方程的解．
5．解分式方程： － ＝1.
分式方程的实际应用(包头3考，呼和浩特2021.22，赤峰2考)
6. (2021包头23题10分)小刚家到学校的距离是1800米．某天早上，小刚到学校后发现作业本忘在家中，此时离上课还有20分钟，于是他立即按原路跑步回家，拿到作业本后骑自行车按原路返回学校．已知小刚骑自行车时间比跑步时间少用了4.5分钟，且骑自行车的平均速度是跑步的平均速度的1.6倍．(1)求小刚跑步的平均速度；
(2)如果小刚在家取作业本和取自行车共用了3分钟，他能否在上课前赶回学校？请说明理由．
7. (2021泰安)接种新冠疫苗是阻断新型冠状病毒传播的有效途径，针对疫苗急需问题，某制药厂紧急批量生产，计划每天生产疫苗16万剂，但受某些因素影响，有10名工人不能按时到厂．为了应对疫情，回厂的工人加班生产，由原来每天工作8小时增加到10小时，每人每小时完成的工作量不变，这样每天只能生产疫苗15万剂．(1)求该厂当前参加生产的工人有多少人？
解：(1)设该厂当前参加生产的工人有x人，由题意，得 ＝ ，解得x＝30，经检验，x＝30是原分式方程的解，且符合题意．答：该厂当前参加生产的工人有30人；
(2)生产4天后，未到的工人同时到岗加入生产，每天生产时间仍为10小时．若上级分配给该厂共760万剂的生产任务，问该厂共需要多少天才能完成任务？
解：(2)每人每小时的生产数量为16÷8÷40＝0.05(万剂)，设还需要生产y天才能完成任务，由题意，得4×15＋(30＋10)×10×0.05×y＝760，解得y＝35，∴该厂共需35＋4＝39(天)，答：该厂共需要39天才能完成任务．
8. 某公司会计欲查询乙商品的进价(如下表)，发现进货单已被墨水污染．
李师傅：我记得甲商品进价比乙商品进价每件高50%；王师傅：我记得甲商品比乙商品的数量多40件．(1)乙商品的进价是多少？
解：(1)设乙商品的进价为x元/件，则甲商品的进价为(1＋50%)x元/件，根据题意，得 － ＝40，解得x＝40.经检验，x＝40是原分式方程的解，且符合题意，答：乙商品的进价为40元/件．
(2)请你帮会计算出甲商品的进价及甲、乙商品的进货数量．
9．(2021江西)甲，乙两人去市场采购相同价格的同一种商品，甲用2400元购买的商品数量比乙用3000元购买的商品数量少10件．(1)求这种商品的单价；
(2)甲，乙两人第二次再去采购该商品时，单价比上次少了20元/件，甲购买商品的总价与上次相同，乙购买商品的数量与上次相同，则甲两次购买这种商品的平均单价是________元/件，乙两次购买这种商品的平均单价是________元/件．
【解法提示】甲第一次购买的数量为2400÷60＝40(件)，第二次购买的数量为2400÷(60－20)＝60(件)，两次购买这种商品的平均单价为(2400＋2400)÷(60＋40)＝48(元/件)；乙第一次购买的数量为3000÷60＝50件，第二次购买的数量为50件，两次购买这种商品的平均单价为[3000＋(60－20)×50]÷(50＋50)＝50(元/件)．