




2024内蒙古中考数学一轮知识点复习 第16课时 二次函数的实际应用(课件)
展开例1 竖直上抛物体时,物体离地面的高度h(m)与运动时间t(s)之间的关系可以近似地用公式h=-5t2+v0t+h0表示,其中h0(m)是物体抛出时离地面的高度,v0(m/s)是物体抛出时的速度.某人将一个小球从距地面3 m的高处以20 m/s的速度竖直向上抛出,则h与t的函数关系式为__________________.
h=-5t2+20t+3
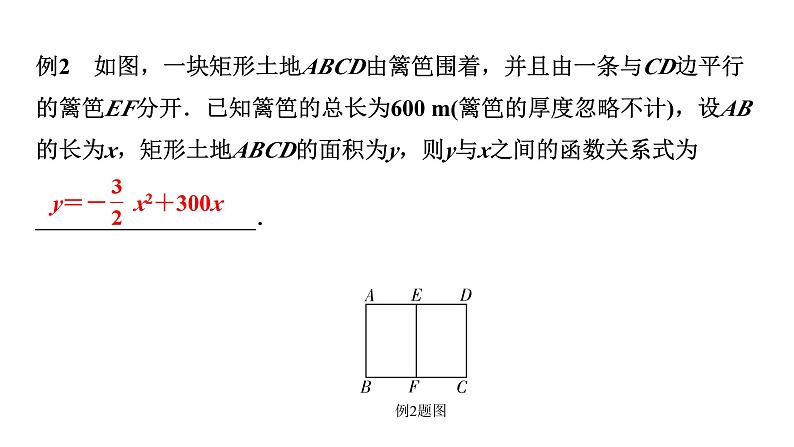
例2 如图,一块矩形土地ABCD由篱笆围着,并且由一条与CD边平行的篱笆EF分开.已知篱笆的总长为600 m(篱笆的厚度忽略不计),设AB的长为x,矩形土地ABCD的面积为y,则y与x之间的函数关系式为 ___________________.
例3 某超市购进一批单价为70元的生活用品,如果按每件100元出售,那么每天可销售20件.经调查发现,这种生活用品的销售单价每降低1元,其销售量相应增加1件,设每天所获利润为W元,当降价x元(x≥8)时,则此时销售量为_____________件,利润W与x之间的函数关系式为______________________.
W=-x2+10x+600
利润=售价-进价;总利润=单件利润×销售量.定价=原售价+涨价;销售量=原销量-少卖的数量.
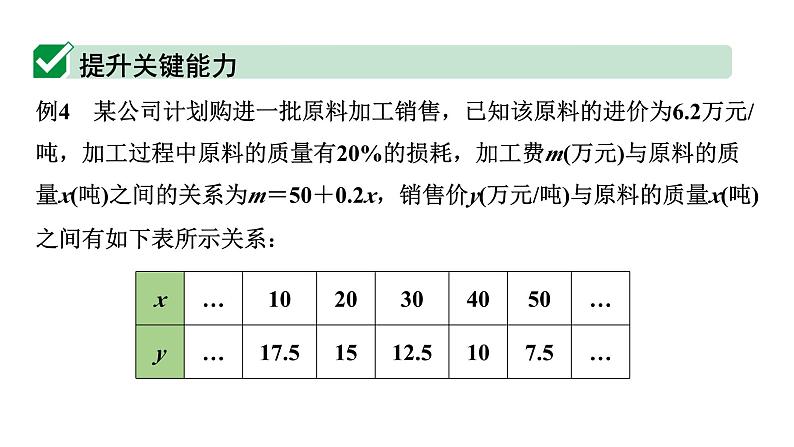
例4 某公司计划购进一批原料加工销售,已知该原料的进价为6.2万元/吨,加工过程中原料的质量有20%的损耗,加工费m(万元)与原料的质量x(吨)之间的关系为m=50+0.2x,销售价y(万元/吨)与原料的质量x(吨)之间有如下表所示关系:
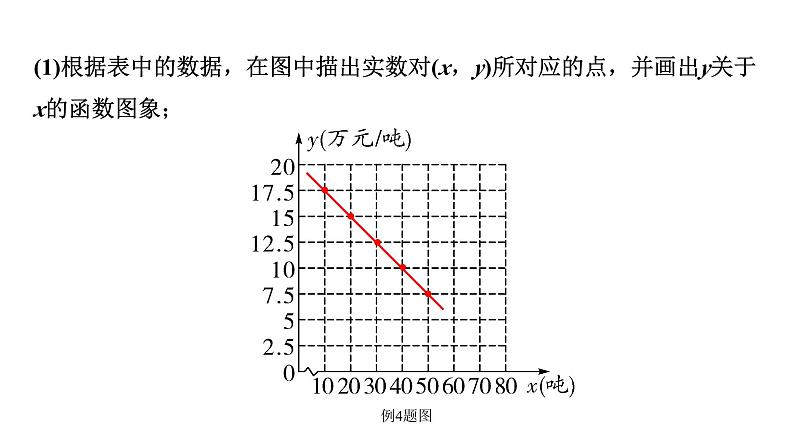
(1)根据表中的数据,在图中描出实数对(x,y)所对应的点,并画出y关于x的函数图象;
(2)根据画出的函数图象,求y与x之间的函数关系式;
【分层分析】设一次函数解析式,从表格中任选两点坐标,利用待定系数法求解即可.
∴y=- x+20,代入其他点均符合此函数关系式,∴y与x之间的函数关系式为y=- x+20;
(3)设销售收入为P(万元),求P与x之间的函数关系式;【分层分析】根据销售收入=销售价×销售量,列出P与x之间的函数关系式.
(4)原料的质量x为多少吨时,所获销售利润最大,最大销售利润是多少万元?(销售利润=销售收入-总支出).
【分层分析】设销售利润为W,根据“销售利润=销售收入-总支出”列关系式,其中销售收入为P,总支出为__________,所以W与x之间的函数关系式为_________________,化为顶点式根据二次函数的性质求解.
W=P-(6.2x+m)
∵- <0,∴当x=24时,W有最大值,W最大=65.2万元.答:原料的质量x为24吨时,所获销售利润最大,最大销售利润是65.2万元.
例5 红星公司销售一种成本为40元/件的产品,若月销售单价不高于50元/件,一个月可售出5万件;月销售单价每涨价1元,月销售量就减少0.1万件.其中月销售单价不低于成本.设月销售单价为x(单位:元/件),月销售量为y(单位:万件).(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
【分层分析】当40≤x≤50时,y=_____,当月销售单价大于50时,月销售单价涨价________元,销售量减少___________万件,则y=___________________,再根据销售量y≥0求出x的取值范围.
5-0.1(x-50)
解:(1)由题知,当40≤x≤50时,y=5,当50<x≤100时,y=5-0.1(x-50)=10-0.1x,∴y与x之间的函数关系式为
(2)当月销售单价是多少元时,月销售利润最大,最大利润是多少万元?【分层分析】设月销售利润为W,根据“利润=(售价-成本)×销售量,分别列出W关于x的关系式,利用函数的性质求解即可.
(2)设月销售利润为W万元,由题意,得当40≤x≤50时,W=(x-40)×5=5x-200,∵5>0,∴当x=50时,W有最大值,W最大=50(万元);当50<x≤100时,
W=(x-40)y =(x-40)(10-0.1x) =-0.1x2+14x-400 =-0.1(x-70)2+90,∵-0.1<0,∴当x=70时,W有最大值,W最大=90(万元),∵50<90,∴当月销售单价是70元/件时,月销售利润最大,最大利润是90万元;
(3)若该公司月销售利润要达到80万元,并让利于民,则月销售单价应为多少元?【分层分析】要使该公司月销售利润达到80万元,则可列方程为_________________________,并根据让利于民得到合适的销售单价.
-0.1x2+14x-400=80
(3)∵该公司月销售利润要达到80万元, ∴50<x≤100.根据题意,得-0.1x2+14x-400=80,解得x1=60,x2=80,∵让利于民,
∴x=60.答:若该公司月销售利润要达到80万元,并让利于民,则月销售单价应为60元;
(4)为响应国家“乡村振兴”政策,该公司决定在某月每销售1件产品便向大别山区捐款a元.已知该公司捐款当月的月销售单价不高于70元/件,月销售最大利润是78万元,求a的值.【分层分析】列出含有未知数a的月销售利润与月销售单价的关系式,再根据月销售单价不高于70元/件和二次函数的性质得到a的值.
∵50<x≤70,∴当月销售单价是70元时,月销售利润最大,即(70-40-a)×(10-0.1×70)=78,解得a=4,∴a的值为4.
1.某出租公司有若干辆同一型号的货车对外出租,每辆货车的日租金实行淡季、旺季两种价格标准,旺季每辆货车的日租金比淡季上涨 .据统计,淡季该公司平均每天有10辆货车未租出,日租金总收入为1500元;旺季所有的货车每天能全部租出,日租金总收入为4000元.
(1)该出租公司这批对外出租的货车共有多少辆?淡季每辆货车的日租金是多少元?
(2)经市场调查发现,在旺季如果每辆货车的日租金每上涨20元,每天租出去的货车就会减少1辆,不考虑其他因素,每辆货车的日租金上涨多少元时,该出租公司的日租金总收入最高?
2. 已知某厂以t小时/千克的速度匀速生产某种产品(生产条件要求0.1
(2)若以生产该产品2小时获得利润1800元的速度进行生产,则1天(按8小时计算)可生产该产品多少千克;
(3)要使生产680千克该产品获得的利润最大,问:该厂应该选取何种生产速度?并求此时最大利润.
3. 如图①是一座抛物线型拱桥侧面示意图.水面宽AB与桥长CD均为24 m,在距离D点6米的E处,测得桥面到桥拱的距离EF为1.5 m,以桥拱顶点O为原点,桥面为x轴建立平面直角坐标系.(1)求桥拱顶部O离水面的距离;
∵AB=CD=24,∴OD=12.∵桥拱顶部离水面的距离为BD的长,∴当x=12时,y1=- ×122=-6,∴桥拱顶部O离水面的距离为6 m.
(2)如图②,桥面上方有3根高度均为4 m的支柱CG,OH,DI,过相邻两根支柱顶端的钢缆呈形状相同的抛物线,其最低点到桥面距离为1 m.①求出其中一条钢缆抛物线的函数表达式;
∴右边钢缆所在的抛物线表达式为y2= (x-6)2+1;(左边钢缆所在的抛物线表达式为y= (x+6)2+1)
2024内蒙古中考数学一轮知识点复习 第12课时 一次函数的实际应用(课件): 这是一份2024内蒙古中考数学一轮知识点复习 第12课时 一次函数的实际应用(课件),共28页。PPT课件主要包含了y=2x+38,例3题图,y=05x+6,例4题解图,300-m,-m≥2m,100-a,n+80,一次函数的实际应用,主叫时间等内容,欢迎下载使用。
2024内蒙古中考数学一轮知识点复习 第8课时 分式方程及其应用(课件): 这是一份2024内蒙古中考数学一轮知识点复习 第8课时 分式方程及其应用(课件),共32页。PPT课件主要包含了分式方程及其应用,考点精讲,解分式方程,未知数,最简公分母,分式方程的实际应用,6-2x,-2x,-4x,x+8等内容,欢迎下载使用。
2024河南中考数学一轮知识点训练复习专题 二次函数的实际应用 (课件): 这是一份2024河南中考数学一轮知识点训练复习专题 二次函数的实际应用 (课件),共34页。PPT课件主要包含了提分特训,一图串考法等内容,欢迎下载使用。












