数学八年级上册1.6 尺规作图多媒体教学ppt课件

这是一份数学八年级上册1.6 尺规作图多媒体教学ppt课件，共21页。PPT课件主要包含了想一想，课堂练习等内容，欢迎下载使用。

（3）在射线AC 上截取AB ＝a ，则线段 AB 就是所要画的线段.
（1）先画射线AC；
（2）用圆规量出线段a的长；
已知：∠AOB ，求作∠AOB 的平分线.
（1）以O 为圆心，以适当长为半径画弧，交OA 于C 点，交OB 于D 点；
（3）过O、P 作射线OP ，则OP即为所求作的角平分线.
你知道什么是尺规作图吗？尺规的基本作用分别是什么？
只用没有刻度的直尺和圆规作图称为尺规作图．尺规作图的工具只能是直尺和圆规,其中直尺用来作直线、线段、射线或延长线段等；圆规用来作圆或圆孤等．值得注意的是直尺是没有刻度的或不考虑刻度的存在.
据传为了显示谁的逻辑思维能力更强，古希腊人限制了几何作图的工具，结果一些普通的画图题让数学家苦苦思索了两千多年.尺规作图特有的魅力，使无数人沉湎其中.
我们已经学习过用直尺和圆规作一条线段等于已知线段及作一个角的平分线. 本节我们将继续学习用直尺和圆规作一个角等于已知角、作一条线段的垂直平分线等基本尺规作图，以及用基本尺规作图作三角形.
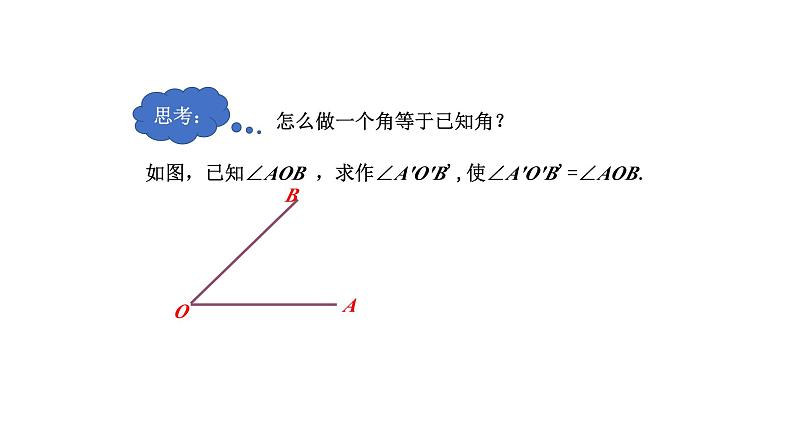
怎么做一个角等于已知角？
如图，已知∠AOB ，求作∠A'O'B',使∠A'O'B'=∠AOB.
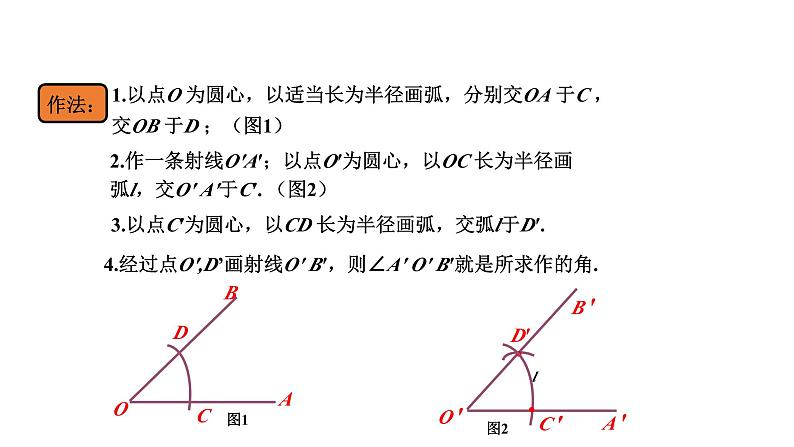
2.作一条射线O′A′；以点O′为圆心，以OC 长为半径画弧l，交O′ A′于C′. （图2）
1.以点O 为圆心，以适当长为半径画弧，分别交OA 于C ，交OB 于D ；（图1）
3.以点C′为圆心，以CD 长为半径画弧，交弧l于D′.
4.经过点O′,D’画射线O′ B′，则∠A′ O′ B′就是所求作的角.
你能证明上题作图的正确性吗?
如图1和图2，连结CD，C’D’
例2 已知线段AB，用直尺和圆规作线段AB的垂直平分线.
分析 要作线段AB的垂直平分线，只需找出线段AB的垂直平分线上的两个点，这由线段垂直平分线上的点的性质不难找出.
（1） 分别以A、B 两点为圆心，以大于AB 线段一 半的长为半径画弧，两弧交于C、D 两点；
（2）过点C、D 作直线CD，直线CD即为所求作线段 AB 的垂直平分线.
你能根据作法证明直线CD就是线段AB的垂直平分线吗？
已知：如图，连接AC、BC、AD、BD，AC=AD=BC=BD．  求证：CD⊥AB，CD平分AB．
例3.已知三角形的两角及其夹边，求作这个三角形. 已知：∠α，∠β，线段a(如图).用直尺和圆规作△ABC，使∠A＝∠α，∠B＝∠β，AB＝a.请按照给出的作法作出相应的图形.
(1)作一条线段AB=a；
(2)分别以A，B为顶点，在AB的同侧作作∠DAB=∠α，∠EBA=∠β，DA与EB相交于点C.
△ABC就是求所作的三角形.
常用的作图语言（1）过点×、×作线段或射线、直线；（2）连结两点×、×；（3）在线段或射线×上截取××=××；（4）以点×为圆心，以××的长为半径作圆（或画弧），交××于点×；（5）分别以点×，点×为圆心，以××，××的长为半径作弧，两弧相交于点×；（6）延长××到点×，使××=××．
注：写作法时，不必重复作图的详细过程，只用一句话概括叙述就可以了．如：作线段××=××；作∠×××=∠×××；作线段××的垂直平分线××等.
1.利用尺规不可作的直角三角形是 （ ）A.已知斜边及一条直角边 B.已知两条直角边C.已知两锐角 D.已知一锐角及一直角边
2.如图，下列四种基本尺规作图分别表示：①作一个角等于已知角；②作一个角的平分线；③作一条线段的垂直平分线；④过直线外一点P作已知直线的垂线．对应选项中作法错误的是(　　)A．① B．② C．③ D．④
3.下列尺规作图，能判断AD是△ABC边上的高的是(　　)
4．已知△ABC(AC＜BC)，用尺规作图的方法在BC上确定一点P，使PA＋PC＝BC，则符合要求的作图痕迹是 (　　)
5.如图，已知线段a，c，∠α.求作△ABC，使BC＝a，AB＝c，∠ABC＝∠α.
解： (1)作∠MBN＝∠α.(2)在射线BM上截取BA＝c，在射线BN上截取BC＝a.(3)连结AC，则△ABC即为所求作的三角形(如图)．