新高考物理一轮复习专题六机械能守恒定律教学课件

这是一份新高考物理一轮复习专题六机械能守恒定律教学课件，共54页。
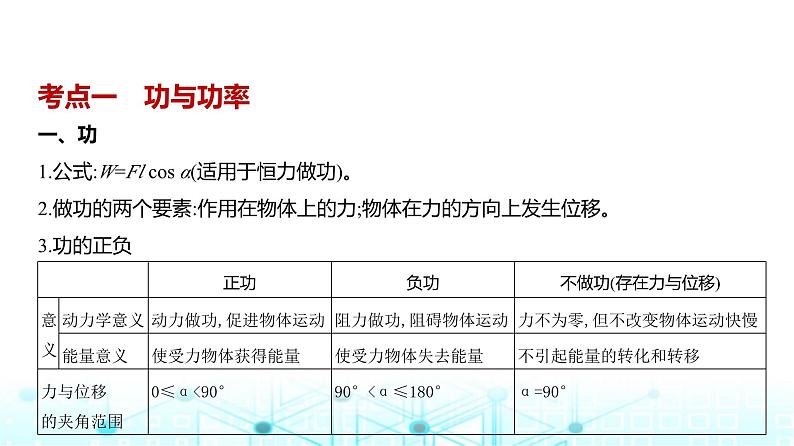
4.一对摩擦力做功的特点
5.合力做功的计算方法 (1)方法一:先求合力F合,再用W合=F合l cs α求功(常用于合力为恒力)。(2)方法二:先求各个力做的功W1,W2,W3,…,再应用W合=W1+W2+W3+…求合力做的功(常 用于多阶段运动过程)。(3)方法三:利用动能定理求合力做功(常用于已知初、末状态的动能)。
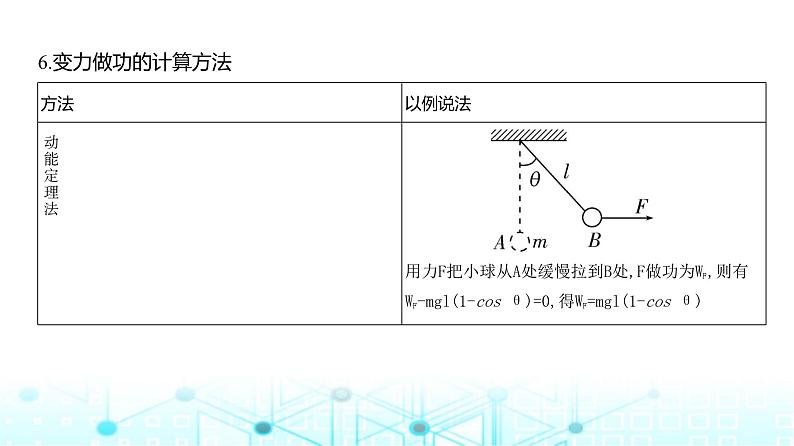
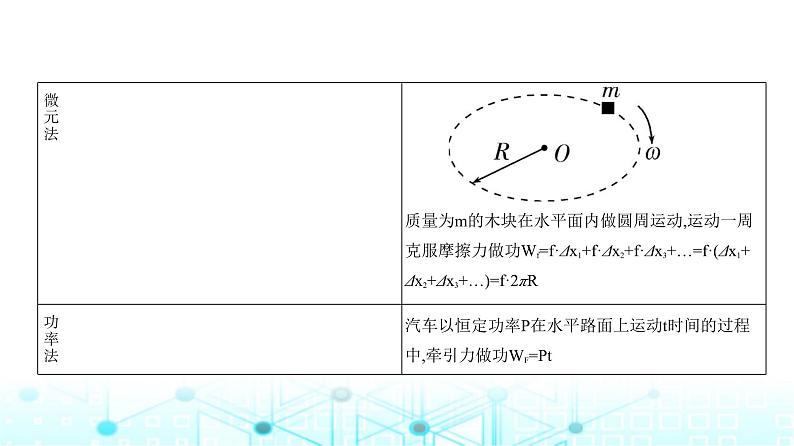
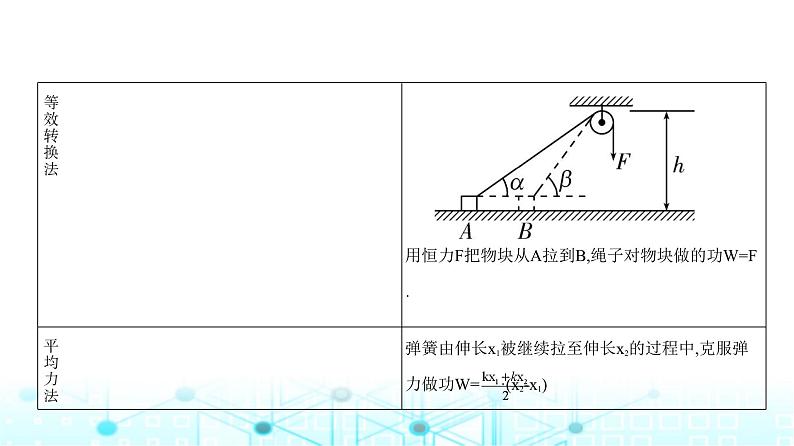
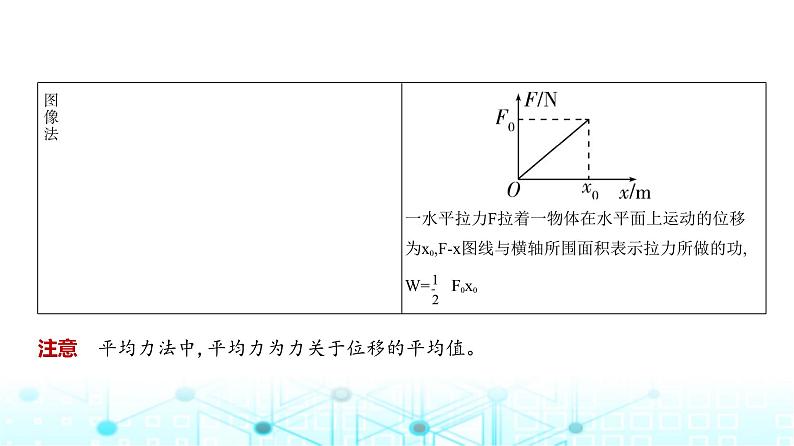
6.变力做功的计算方法
注意　平均力法中,平均力为力关于位移的平均值。
二、功率1.平均功率的计算方法 = , =F  cs α( 为物体运动的平均速度,F为恒力)。2.瞬时功率的计算方法P=Fv cs α(v为该时刻物体的瞬时速度)。
考点二　动能定理及其应用
四、动能定理与图像问题的结合常见图像的分析
例1　如图(a)所示,一物块以一定初速度沿倾角为30°的固定斜面上滑,运动过程中摩 擦力大小f恒定,物块动能Ek与运动路程s的关系如图(b)所示。重力加速度大小取10 m/ s2,物块质量m和所受摩擦力大小f分别为 (　    ) 　     
A.m=0.7 kg,f=0.5 N　　　　    B.m=0.7 kg,f=1.0 NC.m=0.8 kg,f=0.5 N　　　　    D.m=0.8 kg,f=1.0 N
解题指导     ①物块受到的合力②物块速度为零,已到达运动的最高点
  解析    物块上滑阶段受到的合力大小为f+mg sin 30°=  N=4 N,物块下滑阶段受到的合力大小为mg sin 30°-f=  N=3 N,联立可得m=0.7 kg,f=0.5 N,A正确。
考点三　机械能守恒定律
一、重力势能1.重力做功的特点:物体运动时,重力对它做的功只跟它的起点和终点的位置有关,而 跟物体运动的路径无关。2.重力势能的表达式:Ep=mgh(h是物体相对于参考平面的高度)。3.对重力势能的理解(1)系统性:重力势能是由地球与物体所组成的“系统”所共有的。(2)相对性:重力势能的数值与所选参考平面有关,重力势能的变化与参考平面的选取 无关。(3)标矢性:标量,正负表示重力势能的大小。
4.重力势能的变化与重力做功的关系重力对物体做多少正功,物体的重力势能就减少多少;重力对物体做多少负功,物体的 重力势能就增加多少,即WG=-ΔEp。
二、弹性势能1.表达式:Ep= kx2(x是相对弹簧原长的形变量)。2.弹力做功与弹性势能变化的关系:弹力做正功,弹性势能减少;弹力做负功,弹性势能 增加。
三、机械能守恒定律1.内容:在只有重力或弹力做功的物体系统内,动能与势能可以互相转化,而总的机械 能保持不变。2.表达形式(1)守恒观点:E1=E2或Ep1+Ek1=Ep2+Ek2 (需选取零势能面)。(2)转化观点:ΔEk+ΔEp=0(动能与势能间的转化)。(3)转移观点:ΔEA+ΔEB=0(系统内物体间机械能的转移)。提示　机械能守恒是指整个过程中系统机械能保持不变,而非仅初、末状态机械能相等。
3.机械能守恒的判断方法(1)定义法:动能和势能之和始终相等。(2)做功法:①只有重力和系统内的弹力做功;②除重力和系统内的弹力,其他力不做功 或做功的代数和为零。(3)能量转化法:系统与外界无能量交换且无机械能转化。提示　绳子突然绷紧、物体间非弹性碰撞等特定情境,机械能不守恒。4.应用机械能守恒定律解题的一般步骤
例2    如图所示,固定的倾斜光滑杆上套有一个质量为m的圆环,圆环与一橡皮绳相连, 橡皮绳的另一端固定在地面上的A点,橡皮绳竖直时处于原长h。让圆环由静止沿杆滑 下,滑到杆的底端时速度为0。在圆环下滑过程中(　    ) A.圆环的机械能守恒B.橡皮绳的弹性势能一直增大
C.橡皮绳的弹性势能增加了mgh D.橡皮绳再次达到原长时圆环动能最大
  解析    圆环沿杆滑下,滑到杆的底端的过程中有两个力对圆环做功,即圆环受到的重力和橡皮绳的拉力,所以圆环的机械能不守恒,但圆环和橡皮绳组成的系统(以下简称 系统)机械能守恒,故A错误;橡皮绳的弹性势能随橡皮绳的形变量的变化而变化,由题 图知橡皮绳先变松弛后被拉伸,故橡皮绳的弹性势能先不变再增大,故B错误;圆环下滑 过程中系统的机械能守恒,圆环的重力势能减小了mgh,动能变化量为0,则圆环的机械 能减少了mgh,圆环的机械能的减少量等于橡皮绳的弹性势能增加量,橡皮绳的弹性势 能增加了mgh,故C正确;圆环开始下滑至橡皮绳再次达到原长的过程中动能一直增大, 但橡皮绳再次达到原长时圆环动能不是最大,因为当沿杆方向重力的分力大于橡皮绳 弹力的分力时,圆环会继续加速,当沿杆方向合力为零时,圆环的动能最大,故D错误。
易错警示    判断机械能守恒的“两点”注意(1)系统机械能守恒时,机械能一般在系统内物体间转移,其中的单个物体机械能不一 定守恒。(2)机械能守恒的条件绝不是合力做的功等于零,更不是合力等于零,而是只有重力或 系统内弹力做功。
考点四　功能关系　能量守恒
一、功能关系1.对功能关系的理解功是能量转化的量度,做功的过程就是能量转化的过程,不同形式的能量发生相互转 化是通过做功来实现的。做功的多少与能量转化的多少在数值上相等。
2.力学中常见的功能关系
二、能量守恒定律1.定义:能量既不会凭空产生,也不会凭空消失,它只能从一种形式转化为其他形式,或 者从一个物体转移到别的物体,在转化或转移的过程中,能量的总量保持不变。2.对能量守恒定律的两点理解(1)某种形式的能量减少,一定存在其他形式的能量增加,且减少量和增加量一定相等。(2)某个物体的能量减少,一定存在其他物体的能量增加,且减少量和增加量一定相等。3.应用能量守恒定律解题的步骤
二、机车启动问题中的三个重要关系式1.两种启动方式,机车的最大速度都等于其匀速运动时的速度,即vm= 。2.机车以恒定加速度启动的过程中,匀加速过程结束时,功率最大,但此时速度v1= 5 N,假设成立,所以4 s内物体的位移x=vt+ a(4 s-t)2=6 m,物体重力势能增加ΔEp=mgh=mgx sin 37°=36 J,B错误。物体由B点运动到A点,由动能定理可得Wf- mgh=0- mv2,解得整个过程摩擦力对物体做功Wf=34 J,C错误。由题图乙知,0~2 s内,传送带位移x传=6 m,物体位移x物=vt=4 m,二者的相对位移Δx=x传-x物=2 m,产生的热量Q=μ mg cs 37°·Δx=12 J,D正确。
方法技巧　在v-t图像中作出物体的运动图像,阴影部分面积表示0~2 s物体相对传送 带运动的位移大小,可得Δx= ×2×(4-2) m=2 m。也可由图线与时间轴所围的面积,快速得到物体在4 s内的位移x=6 m。
二、板块模型1.动力学角度对滑块和木板进行受力分析,利用牛顿第二定律计算各自的加速度,分析滑块和木板 的运动时间、速度关系和位移关系。可以画出滑块和木板的速度随时间变化的图像, 帮助分析和理解二者的相对运动情况。2.能量角度(1)利用动能定理和功能关系分析滑块和木板各自的能量,分析系统能量的转化和转移。(2)注意区分三个位移(如图所示)
①计算摩擦力对滑块做功时,用滑块相对地面的位移xm;②计算摩擦力对木板做功时,用木板相对地面的位移xM;③计算滑块和木板间因摩擦产生的热量时,用滑块相对木板的位移Δx。 
例3    (多选)如图,一质量为M、长为l的木板静止在光滑水平桌面上,另一质量为m的小 物块(可视为质点)从木板上的左端以速度v0开始运动。已知物块与木板间的滑动摩擦 力大小为f,当物块从木板右端离开时 (　    ) A.木板的动能一定等于flB.木板的动能一定小于flC.物块的动能一定大于 m -fl
D.物块的动能一定小于 m -fl
解题指导    当物块从木板右端离开时”说明小物块和木板并没有达到共同速度,且 离开时小物块的速度vm大于木板的速度vM。
  解析    作木板和物块的v-t图像如图,对木板根据动能定理可得fxM= M ,由于木板的位移xM小于l,所以末态木板的动能一定小于fl,B正确。对小物块根据动能定理可得- fxm= m - m ,由于小物块的位移大于l,所以末态小物块的动能一定小于 m -fl,D正确。 
微专题9    动能定理在多过程问题中的应用动能定理既适用于直线运动,也适用于曲线运动;既适用于恒力做功,也适用于变力做 功;既适用于单过程运动,也适用于多过程运动。1.当物体运动涉及多个阶段和多个过程时,若题目要求计算某一中间物理量,需分阶段 列动能定理;若不需要研究运动的中间状态,可以把多阶段多过程看成一个整体,对全 程列动能定理,从而避开每个运动过程的具体细节。2.思路分析
注意　①各阶段的衔接点起承前启后的作用,往往是题目的突破口。②变力做功容易 出错,需重点分析。
例　如图所示,AB和CDO都是处于同一竖直平面内的光滑圆弧形轨道,O、A位于同一 水平面上。AB是半径为R=1.2 m的 圆周轨道,CDO是半径为r=0.6 m的半圆轨道,最高点O处固定一个竖直弹性挡板(可以把小球弹回且不损失能量,图中没有画出),D为 CDO轨道的中点。BC段是水平粗糙轨道,与圆弧形轨道平滑连接。已知BC段水平轨 道长L=2.5 m,与小球之间的动摩擦因数μ=0.3。现让一个质量为m=1 kg的小球P从A点 的正上方距水平线OA高H处自由落下(取g=10 m/s2,不计空气阻力)。(1)当H=1.8 m时,求小球第一次到达D点时对轨道的压力大小;(2)为使小球与弹性挡板碰撞两次,且小球不会脱离CDO轨道,求H的取值范围。
  解析    (1)小球由释放至第一次到达D点,由动能定理得mg(H+r)-μmgL= m ①,在D点,由牛顿第二定律得FN=m ②,联立①②解得轨道对小球的支持力FN=55 N;由牛顿第三定律得小球对轨道的压力大小FN'=55 N。(2)当H取最小值时,小球刚好运动到O点后第二次与挡板碰撞,由动能定理得mgHmin-3μ mgL= m ③,小球在O点,由牛顿第二定律得mg=m ④,联立解得Hmin=2.55 m;
当H取最大值时,小球与挡板碰撞两次后,再次返回D点速度为零,由动能定理得mg(Hmax +r)-5μmgL=0⑤,解得Hmax=3.15 m;可得H的取值范围为2.55 m≤H≤3.15 m。
  答案    (1)55 N    (2)2.55 m≤H≤3.15 m
微专题10　多物体组成的系统机械能守恒问题
二、隐含条件分析(阻力忽略不计)1.绳子不可伸长,A、B运动过程中速度有什么关系?      2.A、B转动过程中角速度及速率有什么关系? 
提示　杆对物体的作用力并不总是沿杆的方向,杆能对物体做功,单个物体机械能不 守恒。3.A、B运动过程中,速度有什么关系? 　     
  答案    1.A、B速度方向不同,大小相等。2.A、B角速度相等,速率与A、B做圆周运动的半径成正比。3.由关联速度可得,A、B沿绳或沿杆的速度大小相等。
例1　如图所示,在距水平地面高为0.8 m处水平固定着一根长直杆,杆上P点固定一轻 质滑轮,P点右边的杆上套有质量为1 kg的小球B。半径为0.6 m的半圆形细杆竖直固 定在地面上,其圆心O位于P点的正下方,在半圆形细杆最高点处套有质量为2 kg 的小 球A,用一条不可伸长、足够长的柔软细绳绕过定滑轮将两小球连接起来,细绳处于伸 直状态。忽略半圆形细杆的厚度,两小球均可看作质点,不计滑轮的大小和一切摩擦, 重力加速度g取10 m/s2。现小球A受到微小扰动,沿半圆形细杆逆时针运动,在小球A由 最高点运动到半圆形细杆底端的过程中细绳对小球B做的功为 (　    )
A.4 J　　　    B.  J　　　    C.  J　　　    D.  J
  解析    设PA段细绳与竖直方向的夹角为θ,如图所示,当小球A运动到细杆底端时,cs θ= =0.8,由关联速度可得vA cs θ=vB;对小球A和小球B构成的系统,由机械能守恒定律可得mAgR= mA + mB ;对小球B,由动能定理可得W= mB 。联立解得W=  J,D正确。 
三、含弹簧类的多物体系统1.特点由轻弹簧连接的系统,在运动过程中既有重力做功又有弹簧弹力做功,这时系统内物 体间的动能、重力势能和弹性势能相互转化和转移,但总的机械能保持不变。解决此 类问题,往往以分析弹簧的形变量为突破口,通过对弹簧弹性势能的分析找到系统其 他能量的变化情况。2.两点提醒(1)对同一弹簧,弹性势能的大小完全由弹簧的形变量决定,无论弹簧伸长还是压缩。(2)弹簧两端物体把弹簧拉伸至最长(或压缩至最短)时,两端的物体具有相同的速度,弹簧的弹性势能最大。
例2　如图所示,在竖直方向上A、B两物体通过劲度系数为k的轻质弹簧相连,A放在水 平地面上,B、C两物体通过细线绕过轻质定滑轮相连,C放在固定的足够长光滑斜面 上。用手按住C,使细线恰好伸直但没有拉力,并保证ab段的细线竖直、cd段的细线与 斜面平行。已知A、B的质量均为m,C的质量为M(M>2m),细线与滑轮之间的摩擦不计, 开始时整个系统处于静止状态。释放C后它沿斜面下滑,当A恰好要离开地面时,B获得 最大速度(B未触及滑轮,弹簧始终处于弹性限度内,重力加速度大小为g)。求:(1)释放物体C之前弹簧的压缩量;(2)物体B的最大速度vm。