初中数学苏科版九年级下册6.4 探索三角形相似的条件优质ppt课件

这是一份初中数学苏科版九年级下册6.4 探索三角形相似的条件优质ppt课件，文件包含苏科版数学九年级下册641《探索三角形相似的条件一》同步课件pptx、苏科版数学九年级下册641《探索三角形相似的条件-平行线分线段成比例》三大题型原卷版docx、苏科版数学九年级下册641《探索三角形相似的条件-平行线分线段成比例》三大题型解析版docx等3份课件配套教学资源，其中PPT共35页， 欢迎下载使用。

掌握平行线分线段成比例定理及其推论，并能借助此定理或推论推导出更多的线段比例关系
理解相似三角形的预备定理，掌握相似三角形的判定定理（一），并能运用此定理证明两个三角形相似
平行线分线段成比例定理
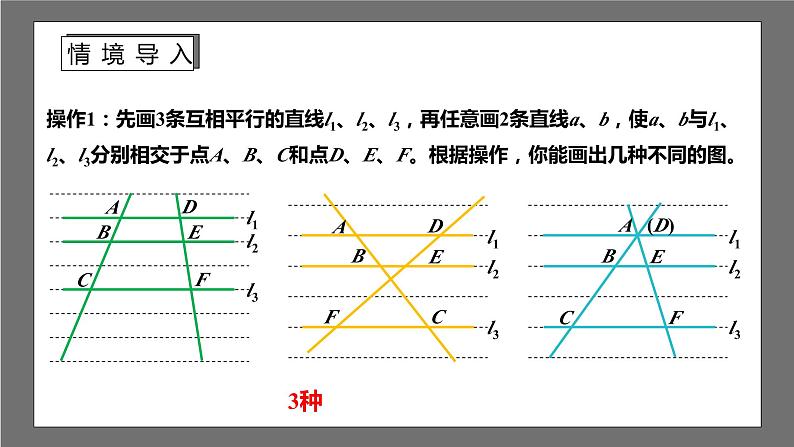
操作1：先画3条互相平行的直线l1、l2、l3，再任意画2条直线a、b，使a、b与l1、l2、l3分别相交于点A、B、C和点D、E、F。根据操作，你能画出几种不同的图。
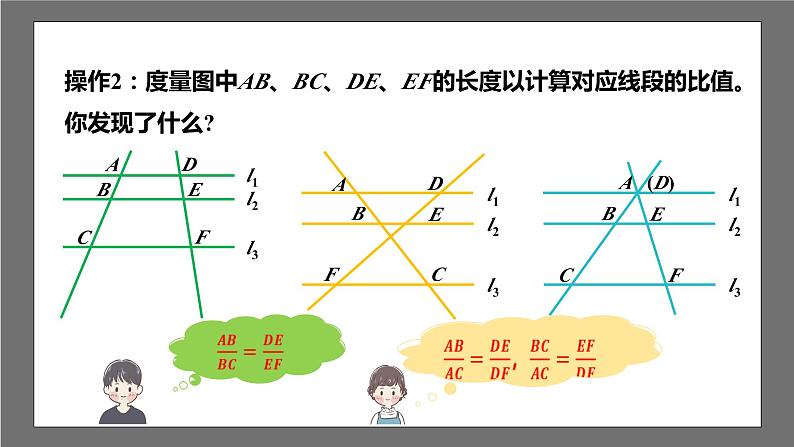
操作2：度量图中AB、BC、DE、EF的长度以计算对应线段的比值。你发现了什么?
两条直线被一组平行线所截，所得的对应线段成比例。
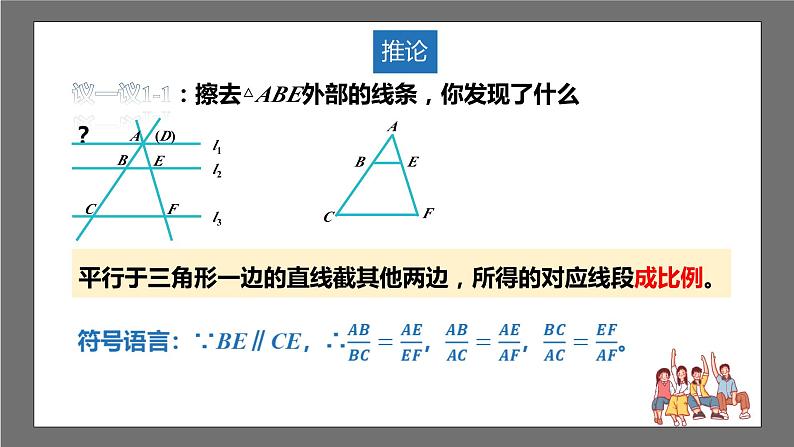
议一议1-1：擦去△ABE外部的线条，你发现了什么？
平行于三角形一边的直线截其他两边，所得的对应线段成比例。
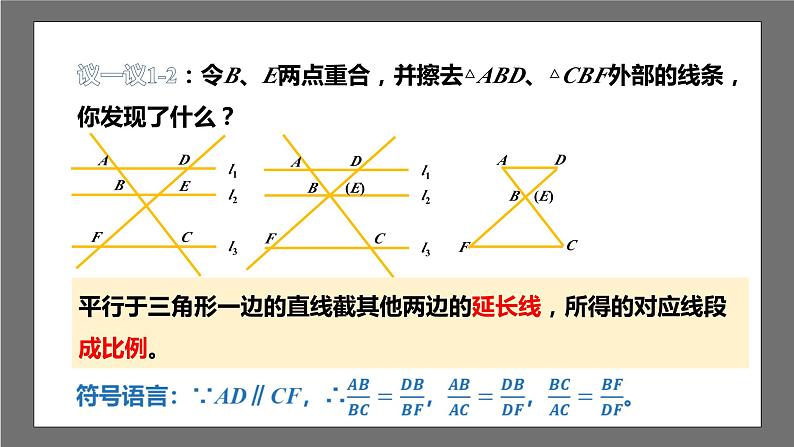
议一议1-2：令B、E两点重合，并擦去△ABD、△CBF外部的线条，你发现了什么？
平行于三角形一边的直线截其他两边的延长线，所得的对应线段成比例。
议一议2-1：度量图中AB、BC、BE、CF的长度并计算对应线段的比值，你发现了什么?
平行于三角形的一边，并且和其他两边相交的直线所截得的三角形的三边与原三角形的三边对应成比例。
如图，过点E作EM∥AC交CF于M，
推论：平行于三角形一边的直线截其他两边（或延长线），所得的对应线段成比例。
结论：平行于三角形的一边，并且和其他两边相交的直线所截得的三角形的三边与原三角形的三边对应成比例。
例1、如图，在△ABC中，E、F分别是AB和AC上的点，且EF∥BC。(1)如果AE=7，EB=5，FC=4，那么AF的长是多少?(2)如果AB=10，AE=6，AF=5，那么FC的长是多少?
例3、如图，△ABC中，∠C=90°，四边形DEFC是内接正方形，BC=4cm，AC=4cm，则正方形面积为________cm²。
例4、如图，在△ABC中，D在AC边上，AD:DC=1:2，O是BD的中点，连接AO并延长交BC于E，则BE:EC=________。
【分析】如图，作DF∥AE交BC于F，
相似三角形的判定定理（一）
Q1：什么叫做相似三角形？
对应角相等、对应边成比例的两个三角形，称为相似三角形
Q2：相似三角形与全等三角形有怎样的关系？
全等三角形一定是相似三角形，相似三角形不一定是全等三角形
Q3：全等三角形的判定定理有哪些？至少需要几个边或角的条件？
SSS、SAS、ASA、AAS、(直角)HL
Q4：相似三角形的判定需要哪些条件呢？
【问题】如图，在△ABC中，DE∥BC，且DE分别交AB、AC于点D、E，△ADE与△ABC有什么关系?
【猜想】△ADE∽△ABC
符号语言：∵DE∥BC，∴△ADE∽△ABC。
平行于三角形一边的直线与其他两边相交，所截得的三角形与原三角形相似。
【观察】如图，两幅三角尺，其中同样角度（30°与60°、或45°与45°）的两个三角尺，它们一定相似吗?
【提问】如果两个三角形有两组角对应相等，它们相似吗？
【探究】(1)作△ABC和△A’B’C’，使得∠A=∠A’，∠B=∠B’，此时∠C=∠C’吗？
∠C=∠C’，理由如下：三角形内角和是180°，知两角相等，即知三角相等。
(3)△ABC和△A’B’C’相似吗？
【猜想】若两个三角形有两组角对应相等，那么它们相似。
【证明】已知：在△ABC和△A’B’C’中，∠A=∠A’，∠B=∠B’，求证：△ABC∽△A’B’C’。
证明：如图，在△ABC的边AB、AC上分别截取AD=A’B’，AE=A’C’，连接DE，
又∵∠B=∠B’∴∠ADE=∠B，∴DE∥BC，∴△ADE∽△ABC【预备定理】，∴△A’B’C’∽△ABC。
符号语言：∵∠A=∠A’，∠B=∠B’，∴△ABC∽△A’B’C’。
两角分别相等的两个三角形相似。
例1、已知：如图，平行四边形ABCD中，E是CB延长线上一点，DE交AB于F，求证：△DAF∽△ECD。
【证明】在平行四边形ABCD中，∵AB∥DC，∴∠CDE=∠AFD，∵∠A=∠C，∴△DAF∽△ECD【判定定理（一）】。
例2、如图所示，已知∠BAC=90°，AB=AC=2，点D在BC上运动（不能到达点B、C），过点D作∠ADE=45°，DE交AC于点E，求证：△ABD∽△DCE。
【证明】∵∠BAC=90°，AB=AC=2，∴∠B=∠C=45°，∵∠ADC=∠B+∠BAD=∠ADE+∠CDE，且∠ADE=45°，∴45°+∠BAD=45°+∠CDE，∴∠BAD=∠CDE，∴△ABD∽△DCE【判定定理（一）】。
例3、如图，△ABC、△DEP是两个全等的等腰直角三角形，∠BAC=∠PDE=90°，(1)若将△DEP的顶点P放在BC上（如图1），PD、PE分别与AC、AB相交于点F、G，求证：△PBG∽△FCP；
证明：(1)如图1，∵△ABC、△DEP是两个全等的等腰直角三角形，∴∠B=∠C=∠DPE=45°，∵∠CPE=∠BGP+∠B=∠CPF+∠DPE，∴∠BGP+45°=∠CPF+45°，∴∠BGP=∠CPF，∵∠B=∠C，∴△PBG∽△FCP【判定定理（一）】；
例3、如图，△ABC、△DEP是两个全等的等腰直角三角形，∠BAC=∠PDE=90°，(2)若使△DEP的顶点P与顶点A重合（如图2），PD、PE与BC相交于点F、G，试问△PBG与△FCP还相似吗？为什么？
(2)△PBG∽△FCP，理由如下：如图2，∵△ABC、△DEP是两个全等的等腰直角三角形，∴∠B=∠C=∠DPE=45°，∵∠PGB=∠C+∠CAE=45°+∠CAE，∠FPC=∠FPG+∠CAE=45°+∠CAE，∴∠PGB=∠FPC，∵∠B=∠C，∴△PBG∽△FCP【判定定理（一）】。
平行线分线段成比例定理：两条直线被一组平行线所截，所得的对应线段成比例。推论：平行于三角形一边的直线截其他两边（或延长线），所得的对应线段成比例。结论：平行于三角形的一边，并且和其他两边相交的直线所截得的三角形的三边与原三角形的三边对应成比例。
相似三角形的预备定理：平行于三角形一边的直线与其他两边相交，所截得的三角形与原三角形相似。判定定理（一）：两角分别相等的两个三角形相似。