2023-2024学年初中下学期八年级数学期末模拟卷（参考答案）（福建）

这是一份2023-2024学年初中下学期八年级数学期末模拟卷（参考答案）（福建），共8页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
二、填空题：本题共6小题，共24分。
11．40° 12．乙 13． 14． 15． 16．60°或120°
三、解答题：本题共9小题，共86分。其中：17-21每题8分，22-23题每题10分，24题12分，25题14分。
17．（8分）
【详解】解：
18．（8分）
【详解】解：在中，根据勾股定理得
，
，
．
19．（8分）
【详解】证明：∵四边形是平行四边形，
∴，，，，
∵平分，平分，
∴，
在和中，
∴
∴，
∴，即．
20．（8分）
【详解】（1）解：∵正比例函数的图象与一次函数的图象交于点，
∴，
∴，
∴，
把点的坐标，代入，
得，
解得，
∴；
（2）解：依题意，把代入，
则，
∴，
∴，
则的面积．
21．（8分）
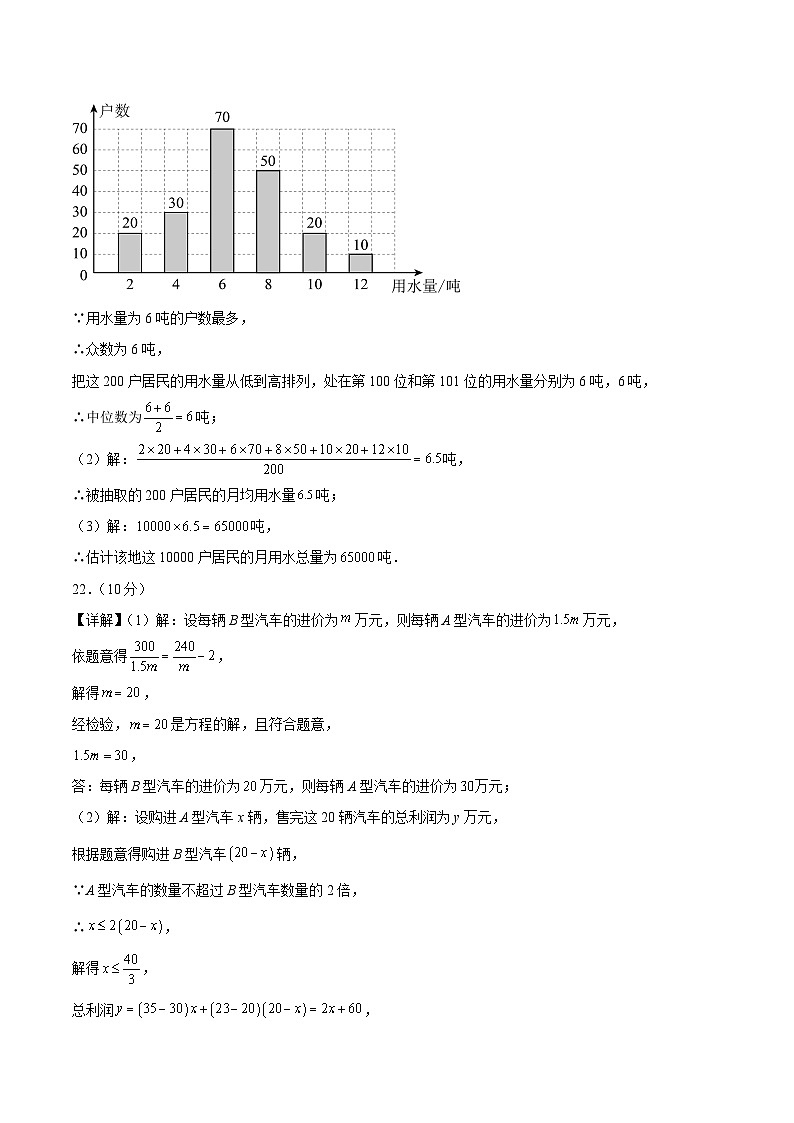
【详解】（1）解：由题意得，，
补全统计图如下：
∵用水量为6吨的户数最多，
∴众数为6吨，
把这200户居民的用水量从低到高排列，处在第100位和第101位的用水量分别为6吨，6吨，
∴中位数为吨；
（2）解：吨，
∴被抽取的200户居民的月均用水量吨；
（3）解：吨，
∴估计该地这10000户居民的月用水总量为吨．
22．（10分）
【详解】（1）解：设每辆B型汽车的进价为万元，则每辆A型汽车的进价为万元，
依题意得，
解得，
经检验，是方程的解，且符合题意，
，
答：每辆B型汽车的进价为万元，则每辆A型汽车的进价为万元；
（2）解：设购进A型汽车x辆，售完这20辆汽车的总利润为y万元，
根据题意得购进B型汽车辆，
∵A型汽车的数量不超过B型汽车数量的2倍，
∴，
解得，
总利润，
∵比例系数，
∴y随x的增大而增大，
又x为正整数，
∴当时，y有最大值，最大值为，
此时B型汽车的数量为辆，
答：该销售中心购进A型汽车13辆，B型汽车7辆，才能使售完这20辆汽车的总利润最大，最大利润是86万元．
23．（10分）
【详解】（1）解：，
数10是“完美勾股数”，
故答案为：是；
（2）证明：
，
，
是“完美勾股数”；
（3）解：由题意得：，
，
，
，
，
，
又，
，即，
，
有一个因式为，
，
∴另一个因式为．
24．（12分）
【详解】（1）解：如图1中，
∵四边形是矩形，
∴，
∴，
由翻折的性质可知：，，
∴，
∴，
∵，
∴；
（2）解：的面积有最小值2，此时．
如图2，，
当，即时，，
取得最小值2，
此时，，
∴四边形是矩形，
∴；
（3）解：如图3，当点与重合时，
由折叠得，
∵
∴
∴
∴，
设，
则，
在中，则有，
解得，
∴，
如图4中，当点运动到时，的值最大，
，
如图5中，当点运动到点落在时，（即），
∴点的运动轨迹，
运动路径．
25．（14分）
【详解】（1）解：，
，，
，（负值舍去），
，；
（2）解：矩形中，
，
由折叠得，
，
，
设，则，
在中，，
，
解得，
点E的坐标为，
设直线的函数解析式为，
将，代入，得：，
解得，
直线的函数解析式为；
（3）解：存在，点P的坐标为或或或．
矩形中，，
，
，
当以O，B，P，F为顶点的四边形为菱形时，存在四种情况，如图：
当为边，为对角线时，,
当点P在点B左侧时，如所示，点坐标为，
当点P在点B右侧时，如所示，点坐标为；
当为边，为对角线时，点P与点B关于x轴对称，如所示，点坐标为；
当为对角线时，如所示，
设，则，
在中，，即，
解得，
可得点坐标为，即，
综上可知，点P的坐标为或或或．1
2
3
4
5
6
7
8
9
10
B
D
C
A
C
B
D
B
A
B