考点串讲03 轴对称【6大考点串讲+14种题型+方法专题+技巧专题+探究专题】-八年级上学期数学期末考点大串讲（人教版）课件PPT

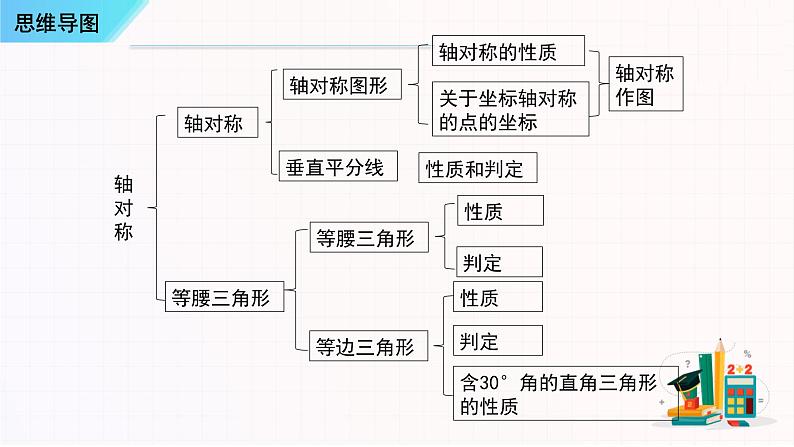
这是一份考点串讲03 轴对称【6大考点串讲+14种题型+方法专题+技巧专题+探究专题】-八年级上学期数学期末考点大串讲（人教版）课件PPT，共50页。PPT课件主要包含了轴对称，等腰三角形，轴对称图形，垂直平分线，等边三角形，轴对称的性质，轴对称作图，性质和判定，思维导图，知识串讲等内容，欢迎下载使用。
关于坐标轴对称的点的坐标
含30°角的直角三角形的性质
如果一个平面图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形就叫做轴对称图形，这条直线就是它的对称轴.这时，我们也说这个图形关于这条直线(成轴)对称.
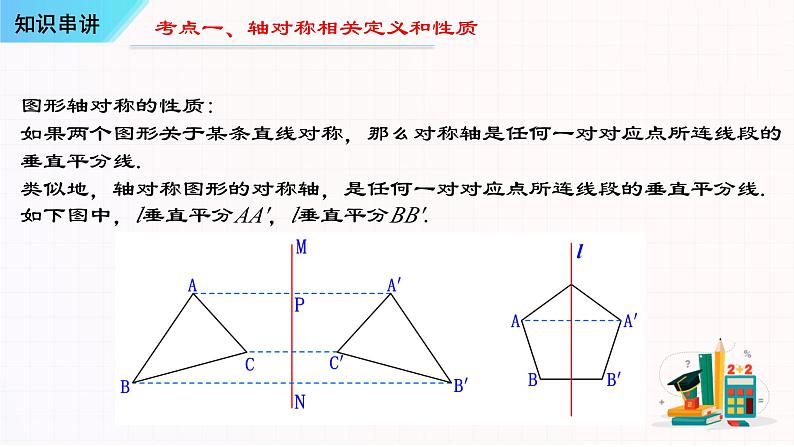
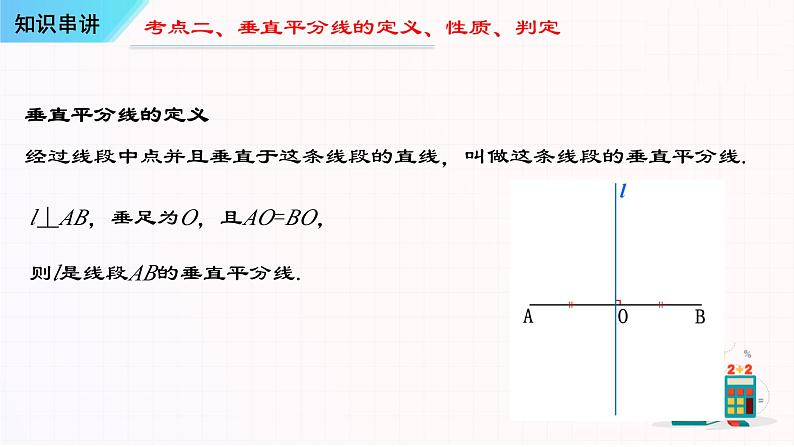
考点一、轴对称相关定义和性质
像这样，把一个图形沿着某一条直线折叠，如果它能与另一个图形重合,那么就说这两个图形关于这条直线(成轴)对称，这条直线叫做对称轴，折叠后重合的点是对应点，叫做对称点.
图形轴对称的性质:如果两个图形关于某条直线对称，那么对称轴是任何一对对应点所连线段的垂直平分线.类似地，轴对称图形的对称轴，是任何一对对应点所连线段的垂直平分线. 如下图中，l垂直平分AA′，l垂直平分BB′.
题型一：能识别轴对称图形．
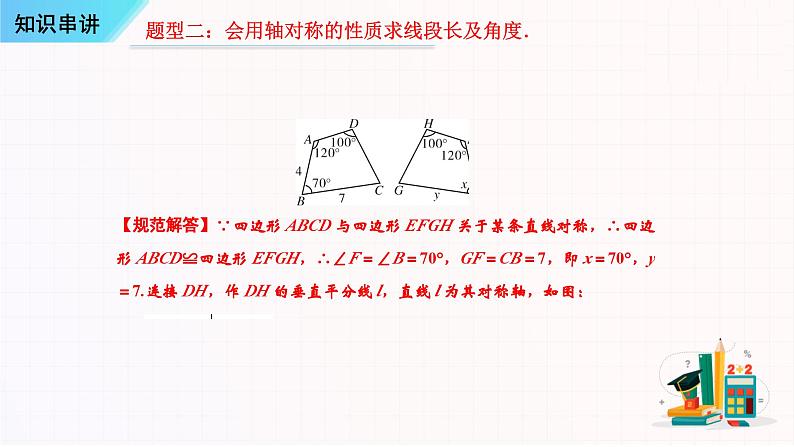
题型二：会用轴对称的性质求线段长及角度．
垂直平分线的定义经过线段中点并且垂直于这条线段的直线，叫做这条线段的垂直平分线.
l⊥AB，垂足为O，且AO=BO，则l是线段AB的垂直平分线.
线段的垂直平分线的性质： 线段垂直平分线上的点与这条线段两个端点的距离相等.
几何符号语言：∵ PC⊥AB，PC平分AB∴ PA=PB
与线段两个端点距离相等的点在这条线段的垂直平分线上.
线段的垂直平分线的判定：
几何符号语言：∵ PA=PB∴ 点P在AB的垂直平分线上
题型三：会用线段的垂直平分线的性质解题．
题型四：会证明线段的垂直平分线．
在平面直角坐标系中，关于 x 轴对称的点横坐标_____，纵坐标___________；关于 y 轴对称的点横坐标___________，纵坐标_____. 点( x ，y )关于 x 轴对称的点的坐标为(___，___) 点( x ，y )关于 y 轴对称的点的坐标为(___，___)
考点三、用坐标表示轴对称
题型五：会画关于坐标轴对称的图形．
性质1:等腰三角形的两个底角相等(简写成“等边对等角”)性质2:等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合(简写成“三线合一”)
考点四、等腰三角形的性质及判定
等腰三角形判定定理： 如果一个三角形有两个角相等，那么这两个角所对的边也相等 (简写成“等角对等边”).
等边三角形的性质：1.等边三角形的三边相等.2.等边三角形的三个内角都相等，并每一个角都等于60°.3.等边三角形的三条高线，三条中线，三条角平分线，分别互相重合.4.等边三角形是轴对称图形，有三条对称轴.
考点五、等边三角形的性质及判定
等边三角形的判定方法：1.三边相等的三角形是等边三角形.2.三个角都相等的三角形是等边三角形.3.有一个角是60°的等腰三角形是等边三角形.
题型六：会利用“等边对等角”解题．
题型七：会灵活运用“三线合一”．
题型八：会判断是否为等腰三角形．
题型九：能综合运用等腰三角形知识解题．
题型十：等边三角形的性质．
题型十一：等边三角形的判定．
含30°角的直角三角形的性质： 在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半.
考点六、含30°角的直角三角形的性质
题型十二：会求线段的长或角的度数．
题型十三：会进行有关证明．
题型十四：会作图确定最短路径．
等腰三角形中的分类讨论
36°、72°、72°或90°、45°、45°
巧用等腰三角形“三线合一”解题
巧作辅助线构造等腰三角形