




专题05 反比例函数(考点清单,7个考点)-九年级上学期数学期末考点大串讲(北师大版)
展开【考点1】反比例函数的相关定义 【考点2】反比例的性质
【考点3】反比例的图像 【考点4反比例函数与一次函数的交点问题】
【考点5】反比例函数中的K值的几何意义
【考点6】反比例函数综合 【考点7】反比例的实际应用
【考点1】反比例函数的相关定义
1.下列函数属于反比例函数的是( )
A.y=B.y=C.y=x2﹣2x﹣1D.y=8x﹣4
【答案】B
【解答】解:A、该函数是正比例函数,故本选项错误;
B、该函数属于反比例函数,故本选项正确;
C、该函数属于二次函数,故本选项错误;
D、该函数属于一次函数,故本选项错误;
故选:B.
2.反比例函数的比例系数是( )
A.2B.﹣2C.﹣1D.1
【答案】B
【解答】解:反比例函数的比例系数是﹣2.
故选:B.
3.下列等式中,a和b成反比例的是( )
A.6×a=B.C.
【答案】C
【解答】解:选项A,B是正比例关系.选项C是反比例关系,
故选:C.
4.反比例函数的比例系数为( )
A.B.﹣3C.﹣5D.
【答案】A
【解答】解:反比例函数的比例系数为:﹣.
故选:A.
5.当三角形的面积一定时,三角形的底和底边上的高成( )关系.
A.正比例函数B.反比例函数
C.一次函数D.二次函数
【答案】B
【解答】解:三角形的底×高=三角形面积×2(定值),
即三角形的底和高成反比例.
故选:B.
6.若反比例函数的图象经过点(﹣2,5),则k的值为 ﹣10 .
【答案】﹣10.
【解答】解:由题意得
∴k=﹣2×5=﹣10,
故答案为:﹣10.
【考点2】反比例的性质
7.对于反比例函数,下列说法中错误的是( )
A.y随x的增大而减小
B.图象分布在一、三象限
C.图象与坐标轴无交点
D.图象于直线y=x对称
【答案】A
【解答】解:∵反比例函数,
∴在每个象限内,y随x的增大而减小,故选项A错误,符合题意;
该函数图象在第一、三象限,故选项B正确,不符合题意;
反比例函数图象坐标轴无交点,故选项C正确,不符合题意;
函数图象关于直线y=x对称,故选项D正确,不符合题意.
故选:A.
8.反比例函数,当x>0时,y随x的增大而增大,那么m的取值范围是( )
A.m<3B.m>3C.m<﹣3D.m>﹣3
【答案】A
【解答】解:∵反比例函数,当x>0时,y随x的增大而增大,
∴m﹣3<0,
∴m<3,
故选:A.
9.若反比例函数的图象在每个象限内,y随x的增大而增大,则k的取值范围为( )
A.k>2B.k<2C.k≥2D.k≤2
【答案】B
【解答】解:∵反比例函数的图象在每个象限内,y随x的增大而增大,
∴k﹣2<0,即k<2.
故选:B.
10.若点A(﹣2,y1)B(2,y2)、C(5,y3)都在反比例函数y=(k>0)的图象上,则y1,y2,y3的大小关系是( )
A.y1<y3<y2B.y1<y2<y3C.y3<y1<y2D.y3<y2<y1
【答案】A
【解答】解:∵反比例函数,
∴此函数图象的两个分支分别位于一、三象限.
∵﹣2<0<2<5,
∴点A(﹣2,y1)位于第三象限,B(2,y2),C(﹣5,y3)位于第一象限,
∴y2>y3>y1.
故选:A.
11.反比例函数的图象一定经过的点是( )
A.(﹣3,﹣2)B.(2,3)C.(2,﹣3)D.(﹣2,﹣4)
【答案】C
【解答】解:反比例函数中,k=﹣6=xy,
A、∵(﹣3)×(﹣2)=6≠﹣6,∴此点不在反比例函数的图象上,故本选项不符合题意;
B、∵2×3=6≠﹣6,∴此点不在反比例函数的图象上,故本选项不符合题意;
C、∵2×(﹣3)=﹣6,∴此点在反比例函数的图象上,故本选项符合题意;
D、∵(﹣2)×(﹣4)=8≠﹣6,∴此点不在反比例函数的图象上,故本选项不符合题意;
故选:C.
12.反比例函数的图象经过点(2,﹣3),则此函数的图象也经过点( )
A.(﹣3,2)B.(﹣2,4)C.(﹣4,﹣2)D.(﹣2,﹣3)
【答案】A
【解答】解:∵反比例函数y=(k≠0)的图象经过点P(2,﹣3),
∴k=2×(﹣3)=﹣6.
A、∵(﹣3)×2=﹣6,∴此点在函数图象上,故本选项正确;
B、∵(﹣2)×4=﹣8≠﹣6,∴此点不在函数图象上,故本选项错误;
C、∵(﹣4)×(﹣2)=8≠﹣6,∴此点不在函数图象上,故本选项错误;
D、∵(﹣2)×(﹣3)=6≠﹣6,∴此点不在函数图象上,故本选项错误.
故选:A.
13.如图,⊙A和⊙B都与x轴和y轴相切,圆心A和圆心B都在反比例函数y=的图象上,则图中阴影部分的面积等于 π .
【答案】见试题解答内容
【解答】解:阴影部分的面积正好构成圆,圆的半径r=1,
则面积S=πr2=π.
故答案为:π.
【考点3】反比例的图像
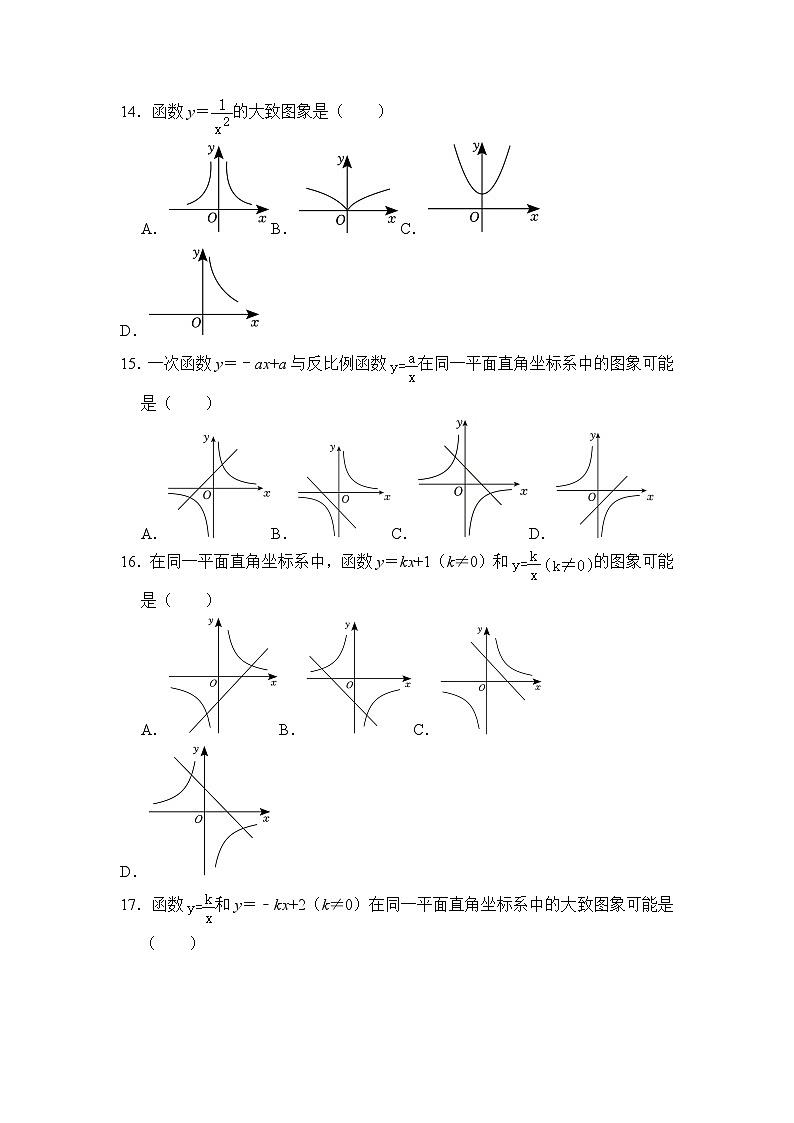
14.函数y=的大致图象是( )
A.B.C.D.
【答案】A
【解答】解:由函数y=可知,函数是双曲线,它的两个分支分别位于第一、二象限,当x>0时,y随x的增大而减小;当x<0时,y随x的增大而增大.
故选:A.
15.一次函数y=﹣ax+a与反比例函数在同一平面直角坐标系中的图象可能是( )
A.B.C.D.
【答案】D
【解答】解:A、双曲线经过第一、三象限,则a>0.则直线应该经过第一、二、四象限,故本选项不符合题意;
B、双曲线经过第一、三象限,则a>0.所以直线应该经过第一、二、四象限,故本选项不符合题意;
C、双曲线经过第二、四象限,则a<0.所以直线应该经过第一、三、四象限,故本选项不符合题意;
D、双曲线经过第二、四象限,则a<0.所以直线应该经过第一、三、四象限,故本选项符合题意.
故选:D.
16.在同一平面直角坐标系中,函数y=kx+1(k≠0)和的图象可能是( )
A.B.C.D.
【答案】D
【解答】解:当k>0时,一次函数y=kx+1经过第一、二、三象限,反比例函数位于第一、三象限;
当k<0时,一次函数y=kx+1经过第一、二、四象限,反比例函数位于第二、四象限;
故选:D.
17.函数和y=﹣kx+2(k≠0)在同一平面直角坐标系中的大致图象可能是( )
A.B.C.D.
【答案】D
【解答】解:在函数(k≠0)和y=﹣kx+2(k≠0)中,
当k>0时,函数(k≠0)的图象位于第一、三象限,函数y=﹣kx+2的图象位于第一、二、四象限,故选项A、B错误,选项D正确,
当k<0时,函数(k≠0)的图象位于第二、四象限,函数y=﹣kx+2的图象位于第一、二、三象限,故选项C错误,
故选:D.
【考点4反比例函数与一次函数的交点问题】
18.若正比例函数y=﹣2x与反比例函数y=的图象交于(1,﹣2),则另一个交点坐标为( )
A.(2,1)B.(﹣1,2)C.(﹣2,﹣1)D.(﹣2,1)
【答案】B
【解答】解:∵正比例函数与反比例函数的图象均关于原点对称,
∴两函数的交点关于原点对称,
∵一个交点的坐标是(1,﹣2),
∴另一个交点的坐标是(﹣1,2).
故选:B.
19.如图,一次函数y=kx+b(k≠0)图象与反比例函数图象交于点A(﹣1,2),B(2,﹣1),则不等式的解集是( )
A.x≤﹣1或x≥2B.﹣1≤x<0或0<x≤2
C.x≤﹣1或0<x≤2D.﹣1≤x<0或x≥2
【答案】D
【解答】解:由函数图象可知,当一次函数y=kx+b(k≠0)图象不在反比例函数图象上方时,x的取值范围是:﹣1≤x<0或x≥2,
∴不等式的解集是:﹣1≤x<0或x≥2,
故选:D.
20.一次函数y1=mx+n和反比例函数的图象如图所示,若y1<y2,则x的取值范围是( )
A.x<﹣2或0<x<1B.﹣2<x<0或x>1
C.x<﹣2或x>1D.﹣2<x<1
【答案】B
【解答】解:当y1<y2,x的取值范围为﹣2<x<0或x>1.
故选:B.
21.如图,一次函数y=kx+b的图象与反比例函数的图象交于A(﹣1,m),(﹣5,n) 两点,则不等式的解集为( )
A.x<﹣5B.x>﹣1
C.﹣5<x<﹣1D.x<﹣5或﹣1<x<0
【答案】D
【解答】解:观察所给函数图象可知,
在直线x=﹣5的左侧部分和直线x=﹣1与直线x=0之间的部分,
一次函数的图象在反比例函数图象的上方,
即,
所以不等式的解集为:x<﹣5或﹣1<x<0.
故选:D.
22.如图,一次函数与反比例函数(x>0)的图象交于点A(1,4),B(4,1)两点,当一次函数大于反比例函数的值时,x的取值范围是( )
A.x<1B.1<x<4C.x>3D.x>4
【答案】B
【解答】解:由图象可知:
当x<1时,反比例函数大于一次函数的函数值,
当x=1时,反比例函数等于一次函数的函数值,
当1<x<4时,一次函数大于反比例函数的函数值,
当x=4时,反比例函数等于一次函数的函数值,
当x>4时,反比例函数大于一次函数的函数值,
即当一次函数大于反比例函数的值时,x的取值范围是:1<x<4,
故选:B
【考点5】反比例函数中的K值的几何意义
23.如图,在平面直角坐标系中,过x轴正半轴上任意一点P作y轴的平行线,分别交函数y=(x>0)、y=﹣(x>0)的图象于点A、点B.若C是y轴上任意一点,则△ABC的面积为( )
A.9B.6C.D.3
【答案】C
【解答】解:连接OA、OB,
∵C是y轴上任意一点,
∴S△AOB=S△ABC,
∵S△AOP=×3=,S△BOP=×|﹣6|=3,
∴S△AOB=S△AOP+S△BOP=+3=,
∴S△ABC=,
故选:C.
24.如图,反比例函数y=在第二象限内的图象如图,点M是图象上一点,MP⊥x轴于点P,如果S△MOP=2,则k= ﹣4 .
【答案】见试题解答内容
【解答】解:根据题意可知,S△MOP=2=|k|,
所以|k|=4,
因为图象在第二象限,
所以k=﹣4.
25.如图,点A在反比例函数的图象上,点B在反比例函数的图象上,且AB∥x轴,点C、D在x轴上,若四边形ABCD为矩形,则它的面积为 2 .
【答案】见试题解答内容
【解答】解:延长BA交y轴于点E,
∵四边形ABCD为矩形,且AB∥x轴,点C、D在x轴上,
∴AE⊥y轴,
∴四边形ADOE与四边形BCOE是矩形,
∵点A在反比例函数的图象上,点B在反比例函数的图象上,
∴S矩形ADOE=1,S矩形BCOE=3,
∴S矩形ABCD=S矩形BCOE﹣S矩形ADOE=3﹣1=2.
故答案为:2.
26.如图,矩形OABC的面积为10,双曲线y=(x>0)与AB、BC分别交于点D、E.若AD=2BD,则k的值为 .
【答案】.
【解答】解:连接OB、OD,
∵矩形OABC的面积为10,
∴S△AOB=S矩形OABC=5,
又∵AD=2BD,
∴S△AOD=2S△BOD,
∴S△AOD=S△AOB==|k|,
∵k>0,
∴k=,
故答案为:.
27.如图,点A,B分别是x轴上的两点,点C,D分别是反比例函数y=(x>0),y=﹣(x<0)图象上的两点,且四边形ABCD是平行四边形,则平行四边形ABCD的面积为 8 .
【答案】8.
【解答】解:解法一:如图,连接OC、OD,CD交y轴于E,
∵点C,D分别是反比例函数y=(x>0),y=﹣(x<0)图象上的两点,
∴S△DOE=×|﹣3|=,S△COE=×5=,
∴S△DOC=+=4=S平行四边形ABCD,
∴S平行四边形ABCD=8,
故答案为:8.
解法二:
设点C的纵坐标为b,
∵点C在反比例函数y=的图象上,
∴点C的横坐标为,
∵四边形ABCD是平行四边形,
∴点D的纵坐标也为b,
∵点D在反比例函数y=﹣(x<0)的图象上,
∴点D的横坐标,
∴CD=﹣=,
∴平行四边形ABCD的面积为×b=8,
故答案为:8.
28.点P,Q,R在反比例函数y=(常数k>0,x>0)图象上的位置如图所示,分别过这三个点作x轴、y轴的平行线.图中所构成的阴影部分面积从左到右依次为S1,S2,S3.若OE=ED=DC,S2+S3=20,则S1的值为 10 .
【答案】10.
【解答】解:∵CD=DE=OE,
∴S1=k,S四边形OGQD=k,
∴S2=(k﹣k×2)=,
S3=k﹣k﹣k=k,
∴k+k=20,
∴k=30,
∴S1=k=10,
故答案为:10.
29.如图,点A、B在反比例函数y=的图象上,A、B的纵坐标分别是2和4,连接OA、OB,则△OAB的面积是 6 .
【答案】6.
【解答】解:过点B作BC⊥x轴于点C,设AD⊥x轴于点D,如图所示:
∵点A、B在反比例函数y=的图象上,
∴△BOC的面积=△AOD的面积==4,
∴△OAB的面积=四边形BCDA的面积,
将A、B的纵坐标2和4,分别代入反比例函数解析式,
得A、B的横坐标分别是4和2,
∴BC=4,AD=2,CD=4﹣2=2,
∴四边形BCDA的面积=(4+2)×2÷2=6,
∴△OAB的面积=6,
故答案为:6.
【考点6】反比例函数综合
30.如图,直线y=mx+n交x轴于点A,交反比例函数y=的图象于C(2,4),D(4,a)两点.
(1)求反比例函数的解析式和a的值;
(2)根据图象直接写出不等式mx+n>的解集;
(3)点M为y轴上任意一点,点N为平面内任意一点,若以C,D,M,N为顶点的四边形是菱形,直接写出点N的坐标.
【答案】(1)y=,a=2;
(2)x<0或2<x<4;
(3)(2,0)或(6,6).
【解答】解:(1)∵点C在反比例函数y=的图象上,
∴4=,
∴k=8,
∴反比例函数的解析式为y=.
∵点D(4,a)在反比例函数y=的图象上,
∴a==2;
(2)观察函数图象可知:当x<0或2<x<4时,直线y=mx+n在反比例函数y=的图象的上方,
∴不等式mx+n>的解集为x<0或2<x<4;
(3)将C(2,4),D(4,2)代入y=mx+n得:,
解得:,
∴直线AB的函数解析式为y=﹣x+6.
当x=0时,y=﹣1×0+6=6,
∴点B的坐标为(0,6),
∴OB=6;
当y=0时,﹣x+6=0,
解得:x=6,
∴点A的坐标为(6,0),
∴OA=6,
∴△AOB为等腰直角三角形.
∵点A的坐标为(6,0),点B的坐标为(0,6),点C的坐标为(2,4),点D的坐标为(4,2),
∴AD==2,CD==2,BC==2,
∴AD=CD=BC,
∴点C,D是线段AB的三等分点.
分两种情况考虑:
①当CD为边时,以点C为圆心,CD的长为半径作圆,交y轴于点B和点M,如图1所示,
∵BD为直径,
∴∠BMD=90°,
∴BM=DM=BD=CD=×2=4,
∴点M的坐标为(0,6﹣4),即(0,2).
设DM的中点为E,则点E的坐标为(,),即(2,2),
∵四边形CMND为菱形,
∴点E为线段CN的中点,
∴点N的坐标为(2×2﹣2,2×2﹣4),即(2,0);
②当CD为对角线时,作线段CD的垂直平分线,交y轴于点M,如图2所示.
设线段CD的中点为F,则点F的坐标为(,),即(3,3),
∵2×3=0+6,2×3=6+0,
∴点F也是线段AB的中点.
∵△AOB为等腰直角三角形,
∴OF垂直平分AB,
∴点M与点O重合.
又∵四边形CMDN为菱形,
∴点F为线段MN的中点,
∴点N的坐标为(2×3﹣0,2×3﹣0),即(6,6).
综上所述,点N的坐标为(2,0)或(6,6).
31.如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)与反比例函数y=(m≠0)的图象相交于A、B两点,过点A作AD⊥x轴于点D,AO=5,OD=AD,B点的坐标为(﹣6,n)
(1)求一次函数和反比例函数的表达式;
(2)P是y轴上一点,且△AOP是等腰三角形,请直接写出所有符合条件的P点坐标.
【答案】见试题解答内容
【解答】解:(1)∵AD⊥x轴,
∴∠ADO=90°,
在Rt△AOD中,AO=5,OD=AD,
∴AD=4,OD=3,
∴A(3,4),
∴k=3×4=12,
∴y=
又点B在反比例函数上,
∴n==﹣2,
∴B(﹣6,﹣2),
∵点A(3,4),B(﹣6,﹣2)在直线AB上,
∴,
∴,
∴AB直线的表达式为y=x+2;
(2)设点P(0,m),
∵A(3,4),O(0,0),
∴OA=5,OP=|m|,AP=,
∵△AOP是等腰三角形,
∴①当OA=OP时,
∴|m|=5,
∴m=±5,
∴P(0,5)或(0,﹣5),
②当OA=AP时,
∴5=,
∴m=0(舍)或m=8,
∴P(0,8),
③OP=AP时,
∴|m|=,
∴m=,
∴P(0,),
即:当P点坐标为(0,8),(0,5),(0,﹣5)或(0,)时,△AOP是等腰三角形.
32.如图,在平面直角坐标系xOy中,直线AB:y=x﹣4与反比例函数的图象交于A、B两点,与x轴相交于点C,已知点A,B的坐标分别为(6n,2n)和(m,﹣6).
(1)求反比例函数的解析式;
(2)直接写出不等式的解集;
(3)点P为反比例函数图象上任意一点,若S△POC=2S△AOC,求点P的坐标.
【答案】(1)反比例函数的解析式为y=,
(2)不等式x4的解集为﹣2<x<0或x>6;
(3)点P的坐标为(3,4)或(﹣3,﹣4).
【解答】解:(1)把点A(6n,2n)代入直线y=x﹣4得:
2n=6n﹣4,
解得:n=1,
∴点A的坐标为:(6,2),
∵反比例函数y=的图象过点A,
∴k=6×2=12,
即反比例函数的解析式为y=,
(2)把点B(m,﹣6)代入直线y=x﹣4得,﹣6=m﹣4,
解得m=﹣2,
∴B(﹣2,﹣6),
观察函数图象,发现:
当﹣2<x<0或x>6时,一次函数图象在反比例函数图象的上方,
∴不等式x﹣4的解集为﹣2<x<0或x>6;
(3)把y=0代入y=x﹣4得:x﹣4=0,
解得:x=4,
即点C的坐标为:(4,0),
∴S△AOC=4×2=4,
∵S△POC=2S△AOC,
∴S△POC=OC•|yP|=8,即2×|yP|=8,
∴|yP|=4,
当点P的纵坐标为4时,则4=,解得x=3,
当点P的纵坐标为﹣4时,则﹣4=,解得x=﹣3,
∴点P的坐标为(3,4)或(﹣3,﹣4).
33.如图,在平面直角坐标系中,A(8,0)、B(0,6)是矩形OACB的两个顶点,双曲线y=(k≠0,x>0)经过AC的中点D,点E是矩形OACB与双曲线y=的另一个交点.
(1)点D的坐标为 (8,3) ,点E的坐标为 (4,6) ;
(2)动点P在第一象限内,且满足S△POB=S△ODE
①若点P在这个反比例函数的图象上,求点P的坐标;
②若点Q是平面内一点,使得以A、C、P、Q为顶点的四边形是菱形,请你直接写出满足条件的所有点Q的坐标.
【答案】(1)(8,3),(4,6).
(2)①(3,8);
②(3,+6)或(3,﹣)或(3,)或(13,3).
【解答】解:(1)∵四边形OACB是矩形,
∴AC=OB=6,
∴C(8,6),
∵点D是AC的中点,
∴D(8,3),
∴k=8×3=24,
∴y=,
当y=6时,x=4,
∴E(4,6),
故答案为:(8,3),(4,6);
(2)①由题意知,S△ODE=S梯形OACE﹣S△OAD﹣S△ECD
=×(4+8)×6﹣×3﹣
=18,
∵S△PBO=S△ODE.
∴×6×xP=×18,
∴xP=3,
∴y=8,
∴P的坐标为(3,8);
②由①知,点P在直线x=3上,设直线x=3交x轴于H,
当AC=AP=6时,若点P在第一象限,
∴PH==,
∴Q(3,+6),
当点P在第四象限舍去,
当CA=CP时,
同理得,Q(3,﹣),Q'(3,),
当PC=PA时,点P(3,3),
则点Q与P关于AC对称,
∴Q(13,3),
综上,点Q(3,+6)或(3,﹣)或(3,)或(13,3).=
【考点7】反比例的实际应用
34.已知蓄电池的电压U为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系(I=).下列反映电流I与电阻R之间函数关系的图象大致是( )
A.B.
C.D.
【答案】D
【解答】解:∵电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系(I=),R、I均大于0,
∴反映电流I与电阻R之间函数关系的图象大致是D选项,
故选:D.
35.在压力不变的情况下,某物体承受的压强p(单位:Pa)与它的受力面积S(单位:m2)是反比例函数关系,其图象如图所示.下列说法错误的是( )
A.函数解析式为 B.物体承受的压力是100N
C.当p≤500Pa时,S≤0.2m2D.当S=0.5m2时,p=200Pa
【答案】C
【解答】解:设p=,
∵点(0.1,1000)在这个函数的图象上,
∴1000=,
∴k=100,
∴p与S的函数关系式为p=,
故选项A,B不符合题意;
当p=500时,S===0.2,
∴当p≤500Pa时,S≥0.2m2,
故选项C符合题意;
当S=0.5时,p=200Pa,
当S=0.2时,p=
=500,
∴当受力面积S=0.2m2时,压强p=500Pa,
故选项D不符合题意;
故选:C.
36.如图1,工人正在用撬棒撬石头,撬棒是杠杆,O为杠杆的支点.当支点和石头的大小不变时,工人师傅用的力F与其力臂l之间的关系式为F=,其图象如图2所示,点P为F=图象上一点,过点P作PM⊥x轴于点M,S△OPM=20000cm2.若OA=40cm,撬棒与水平地面的夹角为30°,则这块石头重力为 1155 N.
【答案】1155.
【解答】解:根据杠杆均衡公式:F压×OA=F×l,
由图2可知,S△OPM=20000(cm2),
即OM•PM=20000(cm2),
∵OM为力臂l,PF为力F,
∴Fl=20000(cm2),
Fl=40000(N•cm),
若OA=40cm,
解得F压=1000N,
因为夹角为30°,
∴重力==1155N.
故答案为:1155.
37.密闭容器内有一定质量的气体,当容器的体积V(单位:m3)变化时,气体的密度ρ(单位:kg/m3)随之变化.已知密度ρ与体积V是反比例函数关系,它的图象如图所示.
(1)求密度ρ关于体积V的函数解析式.
(2)当V=8m3时,求该气体的密度ρ.
【答案】kg/m3.
【解答】解:(1)设ρ=,
将(4,2.5)代入ρ=得2.5=,
解得k=10,
∴ρ=.
(2)将V=8代入ρ=得ρ=.
∴该气体的密度为kg/m3.
38.问题背景:
同学们一定都熟悉这样一句名言:“给我一个支点,我可以撬动地球!”它道出了“杠杆原理”的意义和价值,如图1,杠杆平衡时,阻力×阻力臂=动力×动力臂.
解决问题:
如图2,小伟用撬棍撬动一块大石头,已知平衡时,阻力F1和阻力臂L1分别为1600N和0.5m.
(1)①求动力F和动力臂L的函数关系式.
②当动力臂为2m时,撬动这块石头高于平衡位置,至少需要的力为 400 N.(直接写出答案)
(2)若想动力F不超过(1)中所用力的一半,则动力臂L至少要加长多少?
【答案】(1)①F=;
②400;
(2)动力臂L至少要加长2m.
【解答】解:(1)①∵阻力F1×阻力臂L1=动力F×动力臂L,阻力F1和阻力臂L1分别为1600N和0.5m,
∴F×L=1600×0.5,
即F=;
②当L=2m时,F==400(N),
故答案为:400;
(2)当F=200N时,即200=,
解得L=4(m),
4﹣2=2(m),
答:动力臂L至少要2m.
40.某动物园根据杠杆原理G1•L1=G2•L2上演了一幕现代版“曹冲称象”,具体做法如下:如图所示,在一根已经水平地挂在起重机上的钢梁的左右两边分别挂上一根弹簧秤(重量可以忽略不计)和装有大象的铁笼,其中弹簧秤与钢梁之间的距离为L1=6m,装有大象的铁笼与钢梁之间的距离为L2=0.2m,已知当钢梁又呈水平状态(铁笼已经离地)时,弹簧秤显示的读数为G1=1200N,装有大象的铁笼及其挂钩的总重量为G2.
(1)求装有大象的铁笼及其挂钩的总重量G2;
(2)若装大象的铁笼固定不动,装有大象的铁笼及其挂钩的总重量不变,那么G1是关于L1的什么函数?直接写出函数解析式;
(3)当L1=8m时,求弹簧秤的显示读数G1,当弹簧秤的显示读数G1=1800N,求L1.
【答案】(1)36000N;
(2)G1 是关于 L1 的反比例函数,
;
(3)当L1=8时,G1=900(N),
当G1=1800时,L1=4m.
【解答】解:(1)把 L1=6m,L2=0.2m,G1=1200 代入 G1⋅L1=G2⋅L2得
1200×6=0.2G2,
G2=36000N,
答:装有大象的铁笼及其挂钩的总重量G2为36000N;
(2)G1 是关于 L1 的反比例函数,
∵G1•L1=G2•L2=1200×6,
∴;
(3)把L1=8代入 ,
解得G1==900(N),
把G1=1800代入 得,
解得L1=4m.
41.近期,流感进入发病高峰期,某校为预防流感,对教室进行熏药消毒,测得药物燃烧后室内每立方米空气中的含药量y(mg)与时间x(min)之间的函数关系如图所示,已知药物燃烧时,满足y=2x;药物燃烧后,y与x成反比例,现测得药物m分钟燃毕,此时室内每立方米空气中的含药量为10mg.请根据图中所提供的信息,解决下列问题:
(1)求m的值,并求当x>m时,y与x的函数表达式;
(2)研究表明,当空气中每立方米的含药量不低于4毫克且持续时间不低于10分钟时,才能有效杀灭空气中的病菌,则此次消毒是否有效?请计算说明.
【答案】(1)m=5;当x>m时,y与x的函数表达式为y=;
(2)此次消毒有效.
【解答】解:(1)把(m,10)代入解析式y=2x得:2m=10,
解得m=5;
设当x>m时,y与x的函数表达式为y=,
把(5,10)代入解析式y=得,k=50,
∴当x>m时,y与x的函数表达式为y=;
(2)把y=4代入y=2x得:x=2;
把y=4代入y=得:4=,
解得x=,
∵﹣2=>10,
∴此次消毒有效.
专题08 圆(考点清单,12个考点)-九年级上学期数学期末考点大串讲(北师大版): 这是一份专题08 圆(考点清单,12个考点)-九年级上学期数学期末考点大串讲(北师大版),文件包含专题08圆考点清单12个考点原卷版docx、专题08圆考点清单12个考点解析版docx等2份试卷配套教学资源,其中试卷共68页, 欢迎下载使用。
专题04 图形的相似(考点清单,11个考点)-九年级上学期数学期末考点大串讲(北师大版): 这是一份专题04 图形的相似(考点清单,11个考点)-九年级上学期数学期末考点大串讲(北师大版),文件包含专题04图形的相似考点清单11个考点原卷版docx、专题04图形的相似考点清单11个考点解析版docx等2份试卷配套教学资源,其中试卷共46页, 欢迎下载使用。
考点串讲05 反比例函数【4大考点】-九年级上学期数学期末考点大串讲(北师大版)课件PPT: 这是一份考点串讲05 反比例函数【4大考点】-九年级上学期数学期末考点大串讲(北师大版)课件PPT,共21页。PPT课件主要包含了第六章反比例函数,期末复习,理解反比例函数的概念等内容,欢迎下载使用。












