




专题07 二次函数(考点清单,9个考点)-九年级上学期数学期末考点大串讲(北师大版)
展开【考点1】二次函数的相关概念 【考点2】二次函数的性质
【考点3】二次函数的图像 【考点4】二次函数与系数的关系
【考点5】待定系数法求二次函数解析式
【考点6】二次函数与一元二次方程关系
【考点7】二次函数与不等式的关系 【考点8】二次函数的实际应用
【考点9】二次函数综合
【考点1】二次函数的相关概念
1.下列各式中,y是关于x的二次函数的是( )
A.B.C.D.
2.若是关于的二次函数,则的值为( )
A.B.0C.2D.
3.二次函数的二次项是 ,一次项系数是 ,常数项是 .
【考点2】二次函数的性质
4.已知二次函数的图象性质,下列说法正确的是( )
A.对称轴为直线 B.顶点为C.最大值是D.开口向上
5.将抛物线向右平移3个单位,再向下平移2个单位,所得抛物线解析式为( )
A.B.
C.D.
6.二次函数的顶点坐标是( )
A.B.C.D.
7.已知点,,在抛物线上,则,,的大小关系为( )
A.B.
C.D.
8.二次函数图象是抛物线,.白变量x与函数y的部分对应值如下表:
下列说法不正确的是( )
A.抛物线与y轴的交点坐标为B.抛物线的对称轴是
C.函数y的最小值为D.当时,y随x的增大而增大
9.对于二次函数的图象,下列叙述正确的是( )
A.开口向下B.当时,y随x增大而减小
C.顶点坐标为D.对称轴为直线
10.某超市销售某款商品每天的销售利润(元)与单价(元)之间的函数关系式为,则销售这款商品每天的最大利润为( )
A.5元B.125元C.150元D.200元
【考点3】二次函数的图像
11.关于x的二次函数和一次函数(a,c都是常数,且)在同一平面直角坐标系中的图象可能是( )
A. B. C. D.
12.函数和在同一平面直角坐标系内的图像大致是( )
A.B.C.D.
13.函数与的图象可能是( )
A.B.C.D.
14.函数与的图象可能是( )
A.B.C.D.
【考点4】二次函数与系数的关系
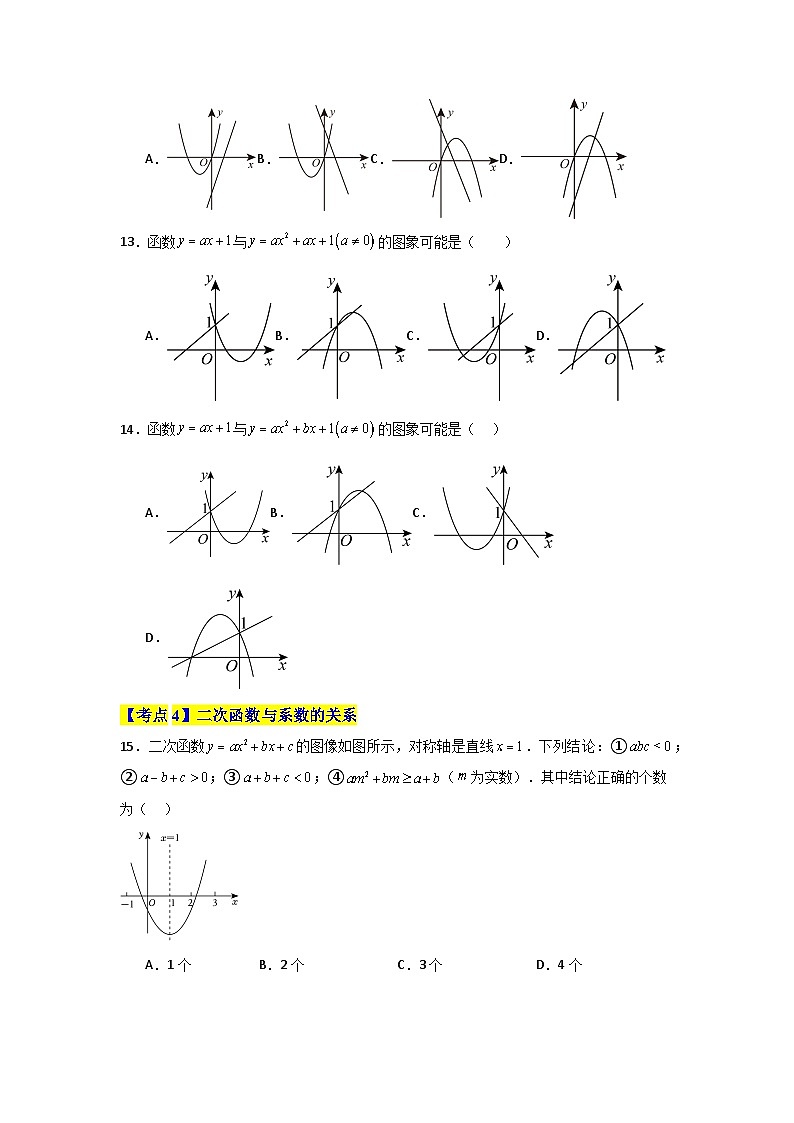
15.二次函数的图像如图所示,对称轴是直线.下列结论:①;②;③;④(为实数).其中结论正确的个数为( )
A.1个B.2个C.3个D.4个
16.抛物线的部分图象如图所示,对称轴为直线,下列说法正确的是( )
A.B.C.D.
26.如图为二次函数的图象,对称轴是,则下列说法:①;②;③;④;⑤(常数).其中正确的个数为( )
A.2B.3C.4D.5
17.如图,抛物线的对称轴是直线,且抛物线与x轴交于A,B两点,若,则下列结论中:①;②;③;④;⑤若m为任意实数,则.正确的个数是( )
A.1B.2C.3D.4
18.如图,已知二次函数的图象如图所示,其对称轴为直线,以下4个结论:①;②;③,其中;④.其中正确结论的有( )
A.4个B.3个C.2个D.1个
【考点5】待定系数法求二次函数解析式
19.将二次函数的图象绕点旋转得到的图象满足的解析式为( )
A.B.
C.D.
20.抛物线与x轴的两个交点为,,其形状和开口方向与抛物线相同,则抛物线的表达式为( )
A.B.
C.D.
21.若抛物线的顶点坐标是且经过点,则该抛物线的解析式为( )
A.B.C.D.
22.已知顶点为的抛物线过点,此抛物线的表达式是( )
A.B.
C.D.
23.已知抛物线,经过点和点
(1)求抛物线的解析式;
(2)求抛物线的顶点坐标.
24.已知抛物线的图象经过点(,),(,).
(1)求抛物线的解析式;
(2)当,求的最大值.
25.已知抛物线的顶点坐标为,且过点.
(1)求此抛物线的解析式.
(2)以x轴为对称轴,将抛物线进行轴对称变换,求变换后所得到的抛物线解析式.
【考点6】二次函数与一元二次方程关系
26.若二次函数的图象与x轴有交点,则k的取值范围是( )
A. B.且C. D.且
27.抛物线与轴的交点个数是( )
A.无交点B.有且只有一个交点C.有两个不同的交点D.无法确定
28.抛物线与轴的交点个数为( )
A.无交点B.1个C.2个D.3个
29.若抛物线与x轴的交点为,,则关于x的一元二次方程的解为( )
A.,B.C.D.,
39.根据表格估计一元二次方程的一个解的范围是( )
A.B.C.D.
31.根据下列表格对应值:判断关于的方程的一个解的范围是( )
A.B.C.D.
【考点7】二次函数与不等式的关系
32.如图,抛物线与x轴的一个交点坐标为,对称轴为直线,当时,x的取值范围是( )
A.B.C.或D.或
33.如图所示:已知二次函数与一次函数的图象相交于点和,则不等式的取值范围是( )
A.B.C. 或D.
34.如图,已知抛物线与直线交于两点.则关于的不等式的解集是( )
A.或B.或C.D.
35.已知,抛物线的图象如图所示,根据图象回答,当时,x的取值范围是( )
A.B.或C.D.
36.如图为抛物线的一部分,其对称轴为直线,若其与x轴的一交点为,则由图象可知,不等式的解集是( )
A.B.C.或D.
【考点8】二次函数的实际应用
37.草莓是云南多地盛产的一种水果,今年某水果销售店在草莓销售旺季,试销售成本为每千克20元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克40元,经试销发现,销售量y(千克)与销售单价x(元)符合一次函数关系,如图是y与x的函数关系图象.
(1)求y与x的函数解析式;
(2)设该水果销售店试销草莓获得的利润为W元,求W的最大值.
38.某超市在“元宵节”来临前夕,购进一种品牌元宵,每盒进价是20元,超市规定每盒售价不得少于25元.根据以往销售经验发现:当售价定为每盒25元时,每天可卖出250盒,每盒售价每提高1元,每天要少卖出10盒.
(1)试求出每天的销售量y(盒)与每盒售价x(元)之间的函数关系式;
(2)当每盒售价定为多少元时,每天销售的利润P(元)最大?最大利润是多少?
(3)为稳定物价,有关管理部门限定:这种元宵的每盒售价不得高于38元.如果超市想要每天获得不低于2000元的利润,那么超市每天至少销售元宵多少盒?
39.某宾馆有50个房间可供游客居住,当每个房间每天的定价为180元时,房间会全部住满,当每个房间每天的定价增加10元时,就会有一个房间空闲,如果游客居住房间,宾馆需对每个房间每天支出20元的各种费用,设每个房间的定价增加x元,此时入住的房间数为y间,宾馆每天的利润为w元.
(1)直接写出y(间)与x(元)之间的函数关系;
(2)如何定价才能使宾馆每天的利润w(元)最大?
(3)若宾馆每天的利润为10800元,则每个房间每天的定价为多少元?
40.“水幕电影”的工作原理是把影像打在抛物线状的水幕上,通过光学原理折射出图象.水幕是由若干个水嘴喷出的水柱组成的(如图),水柱的最高点为 ,,,水嘴高 .
(1)以 为坐标原点,AB所在的直线为轴,所在的直线为轴,建立平面直角坐标系,求抛物线的解析式;
(2)求水柱落点与水嘴底部的距离 .
41.如图,用一段长为米的篱笆围成一个一边靠墙的矩形苗圃园,已知墙长为米,设这个苗圃园垂直于墙的一边长为米.
(1)若苗圃园的面积为平方米,求的值.
(2)若平行于墙的一边长不小于米,当取何值时,这个苗圃园的面积有最大值
【考点9】二次函数综合
42.如图所示,在平面直角坐标系中,抛物线的顶点坐标为,并与轴交于点
(1)求抛物线的解析式;
(2)如图①所示,是抛物线上的一个动点,且位于第一象限,,求的面积的最大值;
(3)如图②所示,在对称轴的右侧作交抛物线于点,直接写出点的坐标.
43.已知,如图,抛物线与轴负半轴交于点,与轴交于,两点,点在点左侧.点的坐标为,.
(1)求抛物线的解析式;
(2)若点是第三象限抛物线上的动点,当四边形面积最大时,求出此时面积的最大值和点的坐标.
(3)将抛物线向右平移个单位,平移后的抛物线与原抛物线相交于点,在原抛物线的对称轴上,为平移后的抛物线上一点,当以、、、为顶点的四边形是平行四边形时,直接写出点的坐标.
44.如图1在平面直角坐标系中,直线分别与x轴,y轴交于点A,B,抛物线经过点B,且与直线的另一个交点为.
(1)求抛物线的解析式;
(2)如图2,点D是抛物线上一动点,且点D的横坐标为,求面积的最大值;
(3)抛物线的对称轴上是否存在一点P,使得是以为直角边的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.
45.如图①,已知抛物线与轴交于两点,与轴交于点.
(1)求该抛物线的表达式;
(2)若点是抛物线上第一象限内的一个动点,连接.当的面积等于面积的倍时,求点的坐标;
(3)抛物线上是否存在点,使得?若存在,请求出点的坐标;若不存在,请说明理由.x
…
0
1
2
…
y
…
4
0
0
4
…
x
0.01
0.03
专题08 圆(考点清单,12个考点)-九年级上学期数学期末考点大串讲(北师大版): 这是一份专题08 圆(考点清单,12个考点)-九年级上学期数学期末考点大串讲(北师大版),文件包含专题08圆考点清单12个考点原卷版docx、专题08圆考点清单12个考点解析版docx等2份试卷配套教学资源,其中试卷共68页, 欢迎下载使用。
专题05 反比例函数(考点清单,7个考点)-九年级上学期数学期末考点大串讲(北师大版): 这是一份专题05 反比例函数(考点清单,7个考点)-九年级上学期数学期末考点大串讲(北师大版),文件包含专题05反比例函数考点清单7个考点原卷版docx、专题05反比例函数考点清单7个考点解析版docx等2份试卷配套教学资源,其中试卷共42页, 欢迎下载使用。
专题04 图形的相似(考点清单,11个考点)-九年级上学期数学期末考点大串讲(北师大版): 这是一份专题04 图形的相似(考点清单,11个考点)-九年级上学期数学期末考点大串讲(北师大版),文件包含专题04图形的相似考点清单11个考点原卷版docx、专题04图形的相似考点清单11个考点解析版docx等2份试卷配套教学资源,其中试卷共46页, 欢迎下载使用。












