华东师大版七年级数学下册专题10.4中心对称【七大题型】(原卷版+解析)

这是一份华东师大版七年级数学下册专题10.4中心对称【七大题型】(原卷版+解析)，共31页。

TOC \ "1-3" \h \u
\l "_Tc20544" 【题型1 中心对称图形的识别】 PAGEREF _Tc20544 \h 1
\l "_Tc9287" 【题型2 根据中心对称的性质判断正误】 PAGEREF _Tc9287 \h 2
\l "_Tc4754" 【题型3 根据中心对称的性质求面积】 PAGEREF _Tc4754 \h 3
\l "_Tc13567" 【题型4 根据中心对称的性质求长度】 PAGEREF _Tc13567 \h 4
\l "_Tc16507" 【题型5 格点中作中心对称图形】 PAGEREF _Tc16507 \h 5
\l "_Tc21933" 【题型6 补全图形使之成为中心对称图形】 PAGEREF _Tc21933 \h 7
\l "_Tc32597" 【题型7 利用中心对称、轴对称、旋转设计图案】 PAGEREF _Tc32597 \h 8
【知识点1 中心对称】
定义：把一个图形绕着某一点旋转180°，如果它能够与另一个图形重合，那么就说这两个图形关于这个点对称或中心对称。这个点叫做对称中心。这两个图形在旋转后能重合的对应点叫做关于对称中心的对称点。
中心对称的性质：①中心对称的两个图形，对称点所连线段都经过对称中心，而且被对称中心所平分；②中心对称的两个图形是全等图形。
【知识点2 中心对称图形】
定义：如果一个图形绕一个点旋转180°后能与自身重合，那么这个图形叫做中心对称图形。这个点叫做它的对称中心。
【题型1 中心对称图形的识别】
【例1】（2022秋·甘肃庆阳·九年级校考期中）教育部门高度重视校园安全教育，要求各级各类学校从认识安全警告标志入手开展安全教育．下列安全图标是中心对称图形的是（ ）
A．注意安全B．急救中心C．水深危险D．禁止攀爬
【变式1-1】（2022秋·广西防城港·九年级统考期中）下列几何图形中，是中心对称图形的是（ ）
A．等边三角形B．等腰梯形C．矩形D．五边形
【变式1-2】（2022秋·云南昭通·九年级统考期中）下列图形中，既是轴对称又是中心对称图形的是（ ）
A．B．
C．D．
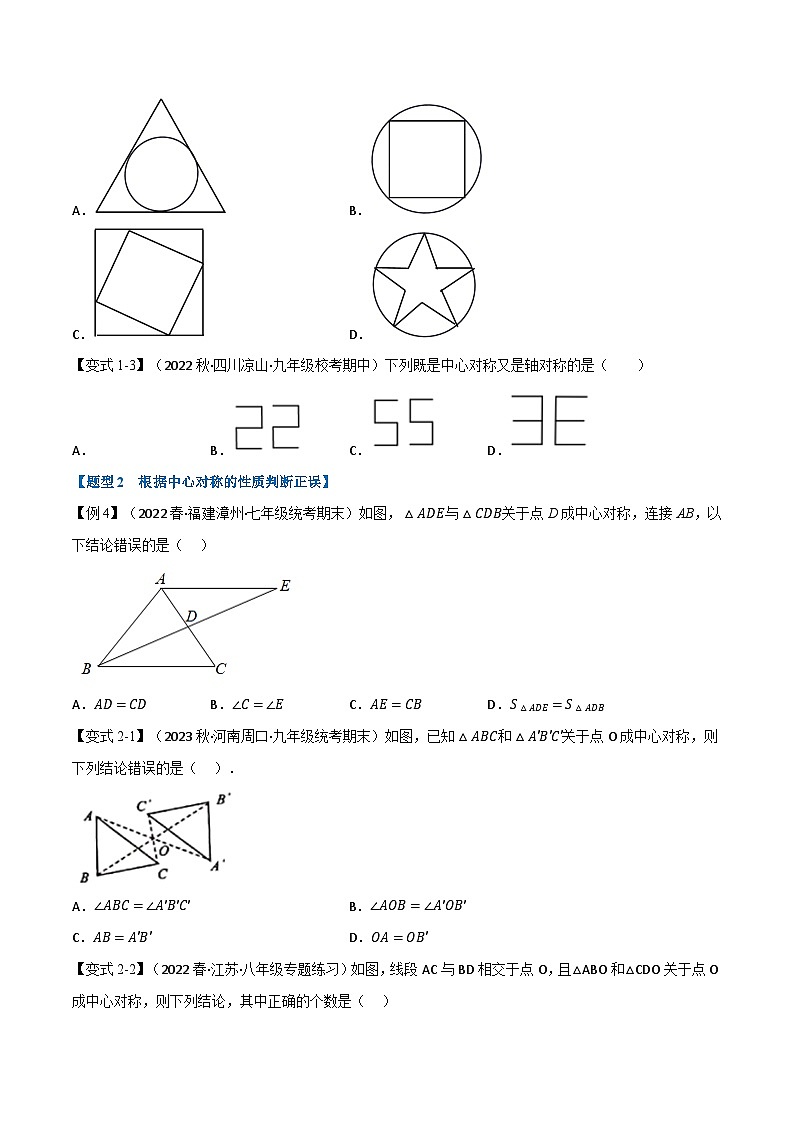
【变式1-3】（2022秋·四川凉山·九年级校考期中）下列既是中心对称又是轴对称的是（ ）
A．B．C．D．
【题型2 根据中心对称的性质判断正误】
【例4】（2022春·福建漳州·七年级统考期末）如图，△ADE与△CDB关于点D成中心对称，连接AB，以下结论错误的是（ ）
A．AD=CDB．∠C=∠EC．AE=CBD．S△ADE=S△ADB
【变式2-1】（2023秋·河南周口·九年级统考期末）如图，已知△ABC和△A′B′C′关于点O成中心对称，则下列结论错误的是（ ）．
A．∠ABC=∠A′B′C′B．∠AOB=∠A′OB′
C．AB=A′B′D．OA=OB′
【变式2-2】（2022春·江苏·八年级专题练习）如图，线段AC与BD相交于点O，且△ABO和△CDO关于点O成中心对称，则下列结论，其中正确的个数是（ ）
①OB＝OD；②AB＝CD；③△ABO≌△CDO；④AC＝BD．
A．4B．3C．2D．1
【变式2-3】（2022春·江苏·八年级专题练习）如图，根据△ABC的已知条件，按如下步骤作图：
（1）以A圆心，AB长为半径画弧；
（2）以C为圆心，CB长为半径画弧，两弧相交于点P；
（3）连接BP，与AC交于点O，连接AP、CP．
以下结论：①BP垂直平分AC；②AC平分∠BAP；③四边形ABCP是轴对称图形也是中心对称图形；④△ABC≌△APC，请你分析一下，其中正确的是（ ）
A．①④B．②③C．①③D．②④
【题型3 根据中心对称的性质求面积】
【例3】（2022秋·广东梅州·九年级校考期中）如图，已知长方形的长为10cm，宽为4cm，则图中阴影部分的面积为（ ）
A．20cm2B．15cm2C．10cm2D．25cm2
【变式3-1】（2022秋·浙江台州·九年级校考期中）如图，直线a、b垂直相交于点O，曲线C关于点O成中心对称，点A的对称点是点A'，AB⊥a于点B，A'D⊥b于点D.若OB=3,OD=2，则阴影部分的面积之和为____.
【变式3-2】（2022秋·山东烟台·八年级统考期末）用四块大正方形地砖和一块小正方形地砖拼成如图所示的实线图案，每块大正方形地砖面积为9，小正方形地砖面积为2，依次连接四块大正方形地砖的中心得到正方形ABCD．则正方形ABCD的面积为_____________．
【变式3-3】（2022·全国·九年级专题练习）如图，正方形ABCD内的图形来自中国古代的太极图，正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称，设黑色部分的面积为S1，正方形的面积为S，则s1s=__．
【题型4 根据中心对称的性质求长度】
【例4】（2022秋·广西河池·九年级统考期中）如图所示的两个三角形是以点A为对称中心的中心对称图形，若∠C=90°，∠B=30°，AC=1，则BD的长度为 _____．
【变式4-1】（2022秋·云南昭通·九年级统考期末）小明、小辉两家所在位置关于学校中心对称．如果小明家距学校3公里，那么他们两家相距_____公里．
【变式4-2】（2022秋·福建龙岩·九年级校考阶段练习）如图，△ABC和△DEF关于某点成中心对称．若AC＝6，AB＝5，BC＝4，求△DEF的周长．
【变式4-3】（2022·山东菏泽·九年级统考期末）如图，小明家的住房平面图呈长方形，被分割成3个正方形和2个长方形后仍是中心对称图形．若只知道原住房平面图长方形的周长，则分割后不用测量就能知道周长的图形的标号为（ ）
A．①②B．②③C．①③D．①②③
【题型5 格点中作中心对称图形】
【例5】（2022春·江西吉安·八年级统考期末）如图是6×5的正方形网格，每个小正方形的顶点称为格点，△ABC的顶点均在格点上．请仅用无刻度的直尺，分别按下列要求作图．
(1)在图1中，作出△ABC关于点O的中心对称图形；
(2)在图2中，取一个格点D，在BC下方作一个与△ABC面积相等的△DBC．
【变式5-1】（2022春·重庆黔江·七年级统考期末）如图所示的方格纸中，每个小正方形的边长都为1，ΔABC与ΔA1B1C1构成中心对称图形．
(1)画出此中心对称图形的对称中心O；
(2)画出将ΔA1B1C1，沿直线DE方向向上平移5格得到的ΔA2B2C2；
(3)要使ΔA2B2C2与ΔCC1C2重合，则ΔA2B2C2绕点C2顺时针方向旋转，至少要旋转 度？(不要求证明)
(4)求ΔCC1C2的面积
【变式5-2】（2022春·重庆沙坪坝·七年级统考期末）如图，在边长为1个单位长度的小正方形组成的网格中，按要求作图并填空．
(1)将四边形ABCD向右平移5个单位长度，得到四边形A1B1C1D1；
(2)作四边形ABCD关于点O成中心对称的四边形A2B2C2D2；
(3)ΔAA1A2的面积为___________．
【变式5-3】（2022春·河南新乡·七年级统考期末）如图，在边长为1个单位长度的8×8的小正方形网格中
(1)将△ABC先向右平移3个单位长度，再向下平移2个单位长度，作出平移后的△A′B′C′；
(2)请画出△A″B″C′，使△A″B″C′和△A′B′C′关于点C′成中心对称
(3)直接写出△A′A″B″的面积．
【题型6 补全图形使之成为中心对称图形】
【例6】（2022秋·黑龙江哈尔滨·九年级校联考期末）图1、图2是8×8的网格，网格中每个小正方形的边长均为1，请按要求画出下列图形，所画图形的各个顶点均在小正方形的顶点上．

(1)在图1中画出以AB为一边的成中心对称的四边形ABCD，使其面积为12；
(2)在图2中画出一个以EF为一边的△EFG，使其是面积为152的轴对称图形．
【变式6-1】（2022秋·吉林松原·九年级统考期中）画图题（按要求画出图形，图①和②都是边长为1个单位的正方形组成）
(1)在图①涂黑一个小正方形和原阴影图形构成中心对称图形．
(2)在图②画出关于直线AC对称的△AB1C再绕点A逆时针旋转90°的△AB2C1．
【变式6-2】（2022秋·北京东城·九年级校考期中）下列3×3网格都是由9个相同小正方形组成，每个网格图中有3个小正方形已涂上阴影，请在余下的6个空白小正方形中，选取1个涂上阴影，使4个阴影小正方形组成一个中心对称图形（画出两种即可）．
【变式6-3】（2022春·陕西咸阳·八年级校联考期中）如图1，是由4个全等的正方形组成的L型图案，请你分别在图2，图3中按下列要求画图：
(1)将图2中的L型图案，添加1个正方形，使它是中心对称图形（不能是轴对称图形）；
(2)将图1的L型图案，改变1个正方形的位置，从而得到一个新的图形，使新图形既是中心对称图形，又是轴对称图形，请在图3中画出改变后的图形．
【题型7 利用中心对称、轴对称、旋转设计图案】
【例7】（2022秋·河北承德·八年级统考期末）认真观察图中阴影部分构成的图案，回答下列问题．
(1)请你写出这四个图案都具有的三个共同特征；
(2)请在图中设计出一个图案，使它也具备你所写出的上述特征．
【变式7-1】（2022秋·上海浦东新·七年级期末）如图1，图2，图3的网格均由边长为1的小正方形组成，图1是三国时期吴国的数学家赵爽所绘制的“弦图”，它由四个形状、大小完全相同的直角三角形组成，赵爽利用这个“弦图”对勾股定理作出了证明，是中国古代数学的一项重要成就，请根据下列要求解答问题．
(1)图1中的“弦图”的四个直角三角形组成的图形是 对称图形（填“轴”或“中心”）．
(2)请将“弦图”中的四个直角三角形通过你所学过的图形变换，在图2，3的方格纸中设计另外两个不同的图案，画图要求：
①每个直角三角形的顶点均在方格纸的格点上，且四个三角形互不重叠，不必涂阴影；
②图2中所设计的图案（不含方格纸）必须是轴对称图形而不是中心对称图形；图3中所设计的图案（不含方格纸）必须既是轴对称图形，又是中心对称图形．
【变式7-2】（2022秋·内蒙古赤峰·八年级统考期末）认真观察下列4个图中阴影部分构成的图案，回答下列问题：
（1）请写出这四个图案都具有的两个共同特征；
（2）请在下图中设计出你心中最美丽的图案，使它也具备你所写出的上述特征．
【变式7-3】（2022春·吉林长春·八年级统考期末）（1）请写出是旋转对称图形的两种多边形（正三角形除外）的名称，并分别写出其旋转角α的最小值；
（2）下面的网格图都是由边长为1的正三角形组成的，请以图中给出的图案为基本图形（其顶点均在格点上），在图2、图3中再分别添加若干个基本图形，使添加的图形与原基本图形组成一个新图案，要求：
①图2中设计的图案既是旋转对称图形又是轴对称图形；
②图3中设计的图案是旋转对称图形，但不是中心对称图形；
③所设计的图案顶点都在格点上，并给图案上阴影（建议用一组平行线段表示阴影）．
专题10.4 中心对称【七大题型】
【华东师大版】
TOC \ "1-3" \h \u
\l "_Tc19163" 【题型1 中心对称图形的识别】 PAGEREF _Tc19163 \h 1
\l "_Tc22494" 【题型2 根据中心对称的性质判断正误】 PAGEREF _Tc22494 \h 4
\l "_Tc10325" 【题型3 根据中心对称的性质求面积】 PAGEREF _Tc10325 \h 6
\l "_Tc4570" 【题型4 根据中心对称的性质求长度】 PAGEREF _Tc4570 \h 9
\l "_Tc16443" 【题型5 格点中作中心对称图形】 PAGEREF _Tc16443 \h 11
\l "_Tc16701" 【题型6 补全图形使之成为中心对称图形】 PAGEREF _Tc16701 \h 16
\l "_Tc29433" 【题型7 利用中心对称、轴对称、旋转设计图案】 PAGEREF _Tc29433 \h 20
【知识点1 中心对称】
定义：把一个图形绕着某一点旋转180°，如果它能够与另一个图形重合，那么就说这两个图形关于这个点对称或中心对称。这个点叫做对称中心。这两个图形在旋转后能重合的对应点叫做关于对称中心的对称点。
中心对称的性质：①中心对称的两个图形，对称点所连线段都经过对称中心，而且被对称中心所平分；②中心对称的两个图形是全等图形。
【知识点2 中心对称图形】
定义：如果一个图形绕一个点旋转180°后能与自身重合，那么这个图形叫做中心对称图形。这个点叫做它的对称中心。
【题型1 中心对称图形的识别】
【例1】（2022秋·甘肃庆阳·九年级校考期中）教育部门高度重视校园安全教育，要求各级各类学校从认识安全警告标志入手开展安全教育．下列安全图标是中心对称图形的是（ ）
A．注意安全B．急救中心C．水深危险D．禁止攀爬
【答案】B
【分析】根据中心对称图形的概念对各选项分析判断即可得解．把一个图形绕某一点旋转180度，如果旋转后的图形能够与原来的图形重合，那么这个图形就叫做中心对称图形．
【详解】解：A选项，是轴对称图形，不符合题意；
B选项，是中心对称图形，符合题意；
C选项，是轴对称图形，不符合题意；
D选项，不是轴对称图形，也不是中心对称图形，不符合题意；
故选：B．
【点睛】本题考查了中心对称图形的概念，掌握中心对称图形是要寻找对称中心，旋转180度后与原图重合是关键．
【变式1-1】（2022秋·广西防城港·九年级统考期中）下列几何图形中，是中心对称图形的是（ ）
A．等边三角形B．等腰梯形C．矩形D．五边形
【答案】C
【分析】根据中心对称图形的概念求解即可．
【详解】解：A．等边三角形不是中心对称图形．故A错误；
B．等腰梯形不是中心对称图形．故B错误；
C．矩形是中心对称图形．故C正确；
D．五边形不是中心对称图形．故D错误．
故选：C．
【点睛】本题主要考查了中心对称图形的知识，掌握中心对称图形是要寻找对称中心，旋转180度后与原图重合是解题的关键．
【变式1-2】（2022秋·云南昭通·九年级统考期中）下列图形中，既是轴对称又是中心对称图形的是（ ）
A．B．
C．D．
【答案】B
【分析】一个图形绕着某固定点旋转180度后能够与原来的图形重合，则称这个图形是中心对称图形，这个固定点叫做对称中心；如果一个图形沿着某条直线对折后，直线两旁的部分能够重合，则称这个图形是轴对称图形，这条直线叫做对称轴；根据中心对称图形与轴对称图形的概念进行判断即可．
【详解】解：A．不是中心对称图形，是轴对称图形，故此选项不合题意；
B．既是中心对称图形，也是轴对称图形，故此选项符合题意；
C．是中心对称图形，不是轴对称图形，故此选项不合题意；
D．不是中心对称图形，是轴对称图形，故此选项不合题意．
故选：B．
【点睛】本题考查的是中心对称图形与轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后与自身重合．
【变式1-3】（2022秋·四川凉山·九年级校考期中）下列既是中心对称又是轴对称的是（ ）
A．B．C．D．
【答案】D
【分析】根据轴对称图形和中心对称图形的概念，对各选项分析判断即可得解．把一个图形绕某一点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形就叫做中心对称图形；如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形．
【详解】解：A、是中心对称图形，不是轴对称图形，故本选项不符合题意；
B、既不是轴对称图形，也不是中心对称图形，故本选项不符合题意；
C、既不是轴对称图形，也不是中心对称图形，故本选项不符合题意；
D、既是中心对称图形又是轴对称图形，故本选项符合题意．
故选：D．
【点睛】本题考查了中心对称图形和轴对称图形，正确掌握相关概念是解题关键．
【题型2 根据中心对称的性质判断正误】
【例2】（2022春·福建漳州·七年级统考期末）如图，△ADE与△CDB关于点D成中心对称，连接AB，以下结论错误的是（ ）
A．AD=CDB．∠C=∠EC．AE=CBD．S△ADE=S△ADB
【答案】B
【分析】根据中心对称图形的性质可得结论．
【详解】解：∵△ADE与△CDB关于点D成中心对称，
∴AD=CD，AE=CB，BD=ED
∴S△ADE=S△ADB
∴选项A、C、D正确，选项B错误；
故选B．
【点睛】本题主要考查了中心对称图形的性质，即对应点在同一条直线上，且到对称中心的距离相等．
【变式2-1】（2023秋·河南周口·九年级统考期末）如图，已知△ABC和△A′B′C′关于点O成中心对称，则下列结论错误的是（ ）．
A．∠ABC=∠A′B′C′B．∠AOB=∠A′OB′
C．AB=A′B′D．OA=OB′
【答案】D
【分析】根据三角形和中心对称的性质求解，即可得到答案．
【详解】∵△ABC和△A′B′C′关于点O成中心对称
∴∠ABC=∠A′B′C′
∠AOB=∠A′OB′
AB=A′B′
OA=OA′
OB=OB′
∴OA=OB′错误，其他选项正确
故选：D．
【点睛】本题考查了三角形和中心对称图形的知识；解题的关键是熟练掌握三角形和中心对称图形的性质，从而完成求解．
【变式2-2】（2022春·江苏·八年级专题练习）如图，线段AC与BD相交于点O，且△ABO和△CDO关于点O成中心对称，则下列结论，其中正确的个数是（ ）
①OB＝OD；②AB＝CD；③△ABO≌△CDO；④AC＝BD．
A．4B．3C．2D．1
【答案】B
【分析】根据成中心对称的两个图形的性质解答．
【详解】解：∵△ABO和△CDO关于点O成中心对称，
∴△ABO≌△CDO，
∴OB＝OD，AB＝CD，
而AC＝BD不一定成立，
故选：B．
【点睛】此题考查成中心对称的两个图形的性质：成中心对称的两个图形全等，熟记性质是解题的关键．
【变式2-3】（2022春·江苏·八年级专题练习）如图，根据△ABC的已知条件，按如下步骤作图：
（1）以A圆心，AB长为半径画弧；
（2）以C为圆心，CB长为半径画弧，两弧相交于点P；
（3）连接BP，与AC交于点O，连接AP、CP．
以下结论：①BP垂直平分AC；②AC平分∠BAP；③四边形ABCP是轴对称图形也是中心对称图形；④△ABC≌△APC，请你分析一下，其中正确的是（ ）
A．①④B．②③C．①③D．②④
【答案】D
【分析】由题意得：AB=AP，CB=CP，从而可判断①；根据等腰三角形的性质，可判断②；根据轴对称和中心对称图形的定义，可判断③；根据SSS，可判断④．
【详解】由题意得：AB=AP，CB=CP，
∴点A、C在BP的垂直平分线上，即：AC垂直平分BP，故①错误；
∵AB=AP，AC⊥BP，
∴AC平分∠BAP，故②正确；
∵AC垂直平分BP，
∴点B、P关于直线AC对称，即：四边形ABCP是轴对称图形，但不是中心对称图形，故③错误；
∵AB=AP，CB=CP，AC=AC，
∴△ABC≌△APC，故④正确；
故选D．
【点睛】本题主要考查垂直平分线的判定定理。等腰三角形的性质，轴对称图形和中心对称图形的定义，全等三角形的判定定理，熟练掌握上述判定定理和性质定理，是解题的关键．
【题型3 根据中心对称的性质求面积】
【例3】（2022秋·广东梅州·九年级校考期中）如图，已知长方形的长为10cm，宽为4cm，则图中阴影部分的面积为（ ）
A．20cm2B．15cm2C．10cm2D．25cm2
【答案】A
【详解】由图形可知，长方形的面积=10×4=40cm2，再根据中心对称的性质得，图中阴影部分的面积即是长方形面积的一半，则图中阴影部分的面积=12×40=20cm2，故选A．
【变式3-1】（2022秋·浙江台州·九年级校考期中）如图，直线a、b垂直相交于点O，曲线C关于点O成中心对称，点A的对称点是点A'，AB⊥a于点B，A'D⊥b于点D.若OB=3,OD=2，则阴影部分的面积之和为____.
【答案】6；
【分析】根据中心对称图形的概念，以及长方形的面积公式即可解答．
【详解】解：∵直线a、b垂直相交于点O，曲线C关于点O成中心对称，点A的对称点是点A'，AB⊥a于点B，A'D⊥b于点D，OB=3，OD=2，
∴AB=2，
∴阴影部分的面积之和为3×2=6．
故答案为6．
【点睛】在同一平面内，如果把一个图形绕某一点旋转180度，旋转后的图形能和原图形完全重合，那么这个图形就叫做中心对称图形．
【变式3-2】（2022秋·山东烟台·八年级统考期末）用四块大正方形地砖和一块小正方形地砖拼成如图所示的实线图案，每块大正方形地砖面积为9，小正方形地砖面积为2，依次连接四块大正方形地砖的中心得到正方形ABCD．则正方形ABCD的面积为_____________．
【答案】11
【分析】连接DK，DN，证明S四边形DMNT=S△DKN=14大正方形的面积，即可解决问题．
【详解】解：如图，连接DK，DN，
∵∠KDN=∠MDT=90°，
∴∠KDM=∠NDT，
∵DK=DN，∠DKM=∠DNT=45°，
∴△DKM≌△DNT（ASA），
∴S△DKM=S△DNT，
∴S四边形DMNT=S△DKN=14大正方形的面积，
∴正方形ABCD的面积=4×14×9+2=11．
故答案为：11．
【点睛】本题考查中心对称，全等三角形的判定和性质，图形的拼剪等知识，解题的关键连接DK，DN，构造全等三角形解决问题．
【变式3-3】（2022·全国·九年级专题练习）如图，正方形ABCD内的图形来自中国古代的太极图，正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称，设黑色部分的面积为S1，正方形的面积为S，则s1s=__．
【答案】π8
【分析】设正方形的边长为a，则正方形内切圆的直径为a，由正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称，可得黑色部分的面积为S1=12×圆的面积，分别求得S1和S，即可求得结论.
【详解】设正方形的边长为a，则正方形内切圆的直径为a，
∵正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称，
∴黑色部分的面积为S1=12×圆的面积=12π×（a2）2=πa28，
正方形的面积为S=a2，所以S1S=πa28a2=π8.
故答案为π8．
【点睛】本题主要考查了正方形的内切圆，根据对称性求出黑色阴影部分的面积是解决本题的关键．
【题型4 根据中心对称的性质求长度】
【例7】（2022秋·广西河池·九年级统考期中）如图所示的两个三角形是以点A为对称中心的中心对称图形，若∠C=90°，∠B=30°，AC=1，则BD的长度为 _____．
【答案】4
【分析】根据题意得△ABC是直角三角形，根据∠B=30°，AC=1，可求得AB，而BD=2AB，据此即可求解．
【详解】解：∵∠C=90°，
∴△ABC是直角三角形，
∵∠B=30°，AC=1，
∴AB=2AC=2，
∵所示的两个三角形是以点A为对称中心的中心对称图形，
∴BD=2AB=4，
故答案为：4．
【点晴】本题主要考查了直角三角形的性质，中心对称图形的性质，解题的关键是掌握这些知识点．
【变式4-1】（2022秋·云南昭通·九年级统考期末）小明、小辉两家所在位置关于学校中心对称．如果小明家距学校3公里，那么他们两家相距_____公里．
【答案】6
【分析】根据中心对称图形的性质，得出小明、小辉两家到学校距离相等，即可得出答案．
【详解】解：∵小明、小辉两家所在位置关于学校中心对称，
∴小明、小辉两家到学校距离相等，
∵小明家距学校3公里，
∴他们两家相距：6公里．
故答案为：6．
【点睛】此题主要考查了中心对称图形的性质，根据已知得出小明、小辉两家到学校距离相等是解决问题的关键．
【变式4-2】（2022秋·福建龙岩·九年级校考阶段练习）如图，△ABC和△DEF关于某点成中心对称．若AC＝6，AB＝5，BC＝4，求△DEF的周长．
【答案】△DEF的周长为15
【分析】根据中心对称的性质可知△ABC≌△DEF，即可求出△DEF的周长．
【详解】由题意，△ABC≌△DEF，
∴△DEF的周长＝△ABC的周长＝6+5+4＝15．
【点睛】本题主要考查了中心对称的性质，熟练地掌握中心对称是一种全等的图形变化是解题的关键．
【变式4-3】（2022·山东菏泽·九年级统考期末）如图，小明家的住房平面图呈长方形，被分割成3个正方形和2个长方形后仍是中心对称图形．若只知道原住房平面图长方形的周长，则分割后不用测量就能知道周长的图形的标号为（ ）
A．①②B．②③C．①③D．①②③
【答案】A
【详解】试题分析：如图，
，
∵长方形被分割成3个正方形和2个长方形后仍是中心对称图形，∴A的对应点是A′，B的对应点是B′，∴AB=A′B′，∵①的长和②的边长的和等于原长方形的长，①的宽和②的边长的和等于原长方形的宽，∴①②的周长和等于原长方形的周长，∴分割后不用测量就能知道周长的图形的标号为①②，其余的图形的周长不用测量无法判断．故选A．
考点：1．中心对称；2．应用题；3．综合题．
【题型5 格点中作中心对称图形】
【例5】（2022春·江西吉安·八年级统考期末）如图是6×5的正方形网格，每个小正方形的顶点称为格点，△ABC的顶点均在格点上．请仅用无刻度的直尺，分别按下列要求作图．
(1)在图1中，作出△ABC关于点O的中心对称图形；
(2)在图2中，取一个格点D，在BC下方作一个与△ABC面积相等的△DBC．
【答案】(1)见解析
(2)见解析
【分析】（1）根据中心对称图形的定义确定对称点，连线即可得到对称图形；
（2）设BC的中点为O，利用等腰三角形的性质及中心对称图形的性质得到点D，连线即可．
（1）
解：如图，△A1B1C1为与△ABC关于点O的中心对称图形；
（2）
如图，△BCD即为所求．
【点睛】此题考查了画中心对称图形，中心对称图形的性质，等腰三角形性质的理解，正确理解中心对称的性质是解题的关键．
【变式5-1】（2022春·重庆黔江·七年级统考期末）如图所示的方格纸中，每个小正方形的边长都为1，ΔABC与ΔA1B1C1构成中心对称图形．
(1)画出此中心对称图形的对称中心O；
(2)画出将ΔA1B1C1，沿直线DE方向向上平移5格得到的ΔA2B2C2；
(3)要使ΔA2B2C2与ΔCC1C2重合，则ΔA2B2C2绕点C2顺时针方向旋转，至少要旋转 度？(不要求证明)
(4)求ΔCC1C2的面积
【答案】(1)见解析
(2)见解析
(3)90
(4)5
【分析】（1）对应点连线的交点即为旋转中心；
（2）利用平移变换的性质分别作出点A1,B1,C1的对应点A2,B2,C2即可；
（3）利用旋转变换的性质判断即可；
（4）根据三角形面积公式求解．
（1）
解：如图，连接BB1,CC1交于点O，则点O即为所求；
（2）
解：如图，ΔA2B2C2即为所求；
（3）
解：根据题意得：要使ΔA2B2C2与ΔCC1C2重合，则ΔA2B2C2绕点C2顺时针方向旋转，至少要旋转90度．
故答案为：90；
（4）
解：ΔCC1C2的面积为12×5×2=5．
【点睛】本题考查作图——旋转变换，平移变换等知识，解题的关键是掌握旋转变换，平移变换的性质，属于中考常考题型．
【变式5-2】（2022春·重庆沙坪坝·七年级统考期末）如图，在边长为1个单位长度的小正方形组成的网格中，按要求作图并填空．
(1)将四边形ABCD向右平移5个单位长度，得到四边形A1B1C1D1；
(2)作四边形ABCD关于点O成中心对称的四边形A2B2C2D2；
(3)ΔAA1A2的面积为___________．
【答案】(1)见解析；
(2)见解析；
(3)5
【分析】（1）利用网格特点和平移的性质画出A、B、C、D的对应点A1、B1、C1、D1即可；
（2）利用网格特点和中心对称的性质画出A、B、C、D的对应点A2、B2、C2、D2即可；
（3）根据三角形面积公式计算．
（1）
如图，四边形A1B1C1D1为所作；
（2）
如图，四边形A2B2C2D2为所作；
（3）
ΔAA1A2的面积＝12×5×2＝5．
故答案为：5．
【点睛】本题考查了作图−旋转变换：根据旋转的性质可知，对应角都相等都等于旋转角，对应线段也相等，由此可以通过作相等的角，在角的边上截取相等的线段的方法，找到对应点，顺次连接得出旋转后的图形．也考查了平移变换．
【变式5-3】（2022春·河南新乡·七年级统考期末）如图，在边长为1个单位长度的8×8的小正方形网格中
(1)将△ABC先向右平移3个单位长度，再向下平移2个单位长度，作出平移后的△A′B′C′；
(2)请画出△A″B″C′，使△A″B″C′和△A′B′C′关于点C′成中心对称
(3)直接写出△A′A″B″的面积．
【答案】(1)见解析
(2)见解析
(3)S△A′B″A″=3
【分析】（1）分别作出A，B，C的对应点A′，B′，C′即可．
（2）分别作出A′，B′的对应点A″，B″即可．
（3）利用三角形面积公式即可．
（1）
解：如图，△A′B′C′即为所求．
（2）
如图，△A″B″C′即为所求．
（3）
S△A′B″A″=12×2×3=3．
【点睛】本题考查了中心对称作图，平移变换作图等知识，掌握平移的性质，中心对称的性质是解题的关键．
【题型6 补全图形使之成为中心对称图形】
【例6】（2022秋·黑龙江哈尔滨·九年级校联考期末）图1、图2是8×8的网格，网格中每个小正方形的边长均为1，请按要求画出下列图形，所画图形的各个顶点均在小正方形的顶点上．

(1)在图1中画出以AB为一边的成中心对称的四边形ABCD，使其面积为12；
(2)在图2中画出一个以EF为一边的△EFG，使其是面积为152的轴对称图形．
【答案】(1)见解析
(2)见解析
【分析】（1）作以AB为边且BC边长为4高为3的平行四边形即可得；
（2）根据等腰三角形的腰为5，腰上的高为3，进行画图即可．
（1）解：如图1，▱ABCD即为所求；
（2）解：如图2，等腰△EFG即为所求．
【点睛】本题主要考查了利用图形的基本变换进行作图，作图时需要运用平行四边形的性质以及等腰三角形的性质进行计算，熟知平行四边形是中心对称图形，等腰三角形是轴对称图形是解题的关键．
【变式6-1】（2022秋·吉林松原·九年级统考期中）画图题（按要求画出图形，图①和②都是边长为1个单位的正方形组成）
(1)在图①涂黑一个小正方形和原阴影图形构成中心对称图形．
(2)在图②画出关于直线AC对称的△AB1C再绕点A逆时针旋转90°的△AB2C1．
【答案】(1)见解析
(2)见解析
【分析】（1）直接利用中心对称图形的性质得出符合题意的图形即可；
（2）利用轴对称图形的性质及旋转的性质得出对应点的位置，进而得出答案．
【详解】（1）解：如图，
（2）解：如图，
【点睛】本题考查了旋转变换，轴对称变换，中心对称图形，正确得出对应点的位置是解题的关键．
【变式6-2】（2022秋·北京东城·九年级校考期中）下列3×3网格都是由9个相同小正方形组成，每个网格图中有3个小正方形已涂上阴影，请在余下的6个空白小正方形中，选取1个涂上阴影，使4个阴影小正方形组成一个中心对称图形（画出两种即可）．
【答案】见详解
【分析】利用中心对称图形的性质的出符合题意的答案即可．
【详解】解：在余下的空白小正方形中选取1个涂上阴影，使4个阴影小正方形组成一个中心对称图形，如下图所示．
【点睛】本题主要考查了图形旋转以及中心对称图形的知识，熟练掌握旋转的性质以及中心对称图形的定义是解题关键．
【变式6-3】（2022春·陕西咸阳·八年级校联考期中）如图1，是由4个全等的正方形组成的L型图案，请你分别在图2，图3中按下列要求画图：
(1)将图2中的L型图案，添加1个正方形，使它是中心对称图形（不能是轴对称图形）；
(2)将图1的L型图案，改变1个正方形的位置，从而得到一个新的图形，使新图形既是中心对称图形，又是轴对称图形，请在图3中画出改变后的图形．
【答案】(1)见解析
(2)见解析
【分析】（1）根据轴对称图形的性质，先找出对称轴，再思考如何画图；
（2）根据中心对称和轴对称的性质画一个图形．
（1）
解：如图2所示．
；
（2）
解：如图3所示．
．
【点睛】本题考查了中心对称图形及轴对称图形的性质，及其作图的方法，学生做这些题时找对称轴及对称点是关键．
【题型7 利用中心对称、轴对称、旋转设计图案】
【例7】（2022秋·河北承德·八年级统考期末）认真观察图中阴影部分构成的图案，回答下列问题．
(1)请你写出这四个图案都具有的三个共同特征；
(2)请在图中设计出一个图案，使它也具备你所写出的上述特征．
【答案】(1)特征1：都是轴对称图形；特征2：都是中心对称图形；特征3：这些阴影图案的面积都等于4个小正方形的面积
(2)见解析
【分析】（1）根据轴对称图形以及中心对称的定义解答：沿某条直线折叠后直线两旁的部分能够完全重合的图形叫做轴对称图形；绕一个点旋转180°后所得的图形与原图形完全重合的图形叫做中心对称图形；
（2）画出同时满足轴对称图形和中心对称图形的图形即可．
【详解】（1）（1）特征1：都是轴对称图形；
特征2：都是中心对称图形；
特征3：这些阴影图案的面积都等于4个小正方形的面积；
（2）满足条件的图案有很多，这里画三个，三个都具有上述特征，如图所示：
【点睛】轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合；中心对称图形是要寻找对称中心，旋转180°后两部分重合．
【变式7-1】（2022秋·上海浦东新·七年级期末）如图1，图2，图3的网格均由边长为1的小正方形组成，图1是三国时期吴国的数学家赵爽所绘制的“弦图”，它由四个形状、大小完全相同的直角三角形组成，赵爽利用这个“弦图”对勾股定理作出了证明，是中国古代数学的一项重要成就，请根据下列要求解答问题．
(1)图1中的“弦图”的四个直角三角形组成的图形是 对称图形（填“轴”或“中心”）．
(2)请将“弦图”中的四个直角三角形通过你所学过的图形变换，在图2，3的方格纸中设计另外两个不同的图案，画图要求：
①每个直角三角形的顶点均在方格纸的格点上，且四个三角形互不重叠，不必涂阴影；
②图2中所设计的图案（不含方格纸）必须是轴对称图形而不是中心对称图形；图3中所设计的图案（不含方格纸）必须既是轴对称图形，又是中心对称图形．
【答案】(1)中心
(2)见解析
【分析】（1）利用中心对称图形的意义得到答案即可；
（2）①每个直角三角形的顶点均在方格纸的格点上，且四个三角形不重叠，是轴对称图形；
②所设计的图案（不含方格纸）必须是中心对称图形或轴对称图形．
（1）
图1中的“弦图”的四个直角三角形组成的图形是中心对称图形，
故答案为：中心；
（2）
如图2是轴对称图形而不是中心对称图形；
图3既是轴对称图形，又是中心对称图形．
【点睛】本题考查利用旋转或轴对称设计方案，关键是理解旋转和轴对称的概念，按要求作图即可．
【变式7-2】（2022秋·内蒙古赤峰·八年级统考期末）认真观察下列4个图中阴影部分构成的图案，回答下列问题：
（1）请写出这四个图案都具有的两个共同特征；
（2）请在下图中设计出你心中最美丽的图案，使它也具备你所写出的上述特征．
【答案】（1）特征1：都是轴对称图形；特征2：都是中心对称图形；特征3：这些阴影图案的面积都等于4个小正方形的面积；（2）见解析
【分析】（1）根据轴对称图形以及中心对称的定义解答：沿某条直线折叠后直线两旁的部分能够完全重合的图形叫做轴对称图形；绕一个点旋转180度后所得的图形与原图形完全重合的图形叫做中心对称图形．
（2）画出同时满足轴对称图形和中心对称图形的图形即可．
【详解】解：（1）特征1：都是轴对称图形；
特征2：都是中心对称图形；
特征3：这些阴影图案的面积都等于4个小正方形的面积；
（2）满足条件的图案有很多，这里画三个，三个都具有上述特征，如图所示：
【点睛】轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合；中心对称图形是要寻找对称中心，旋转180度后两部分重合．
【变式7-3】（2022春·吉林长春·八年级统考期末）（1）请写出是旋转对称图形的两种多边形（正三角形除外）的名称，并分别写出其旋转角α的最小值；
（2）下面的网格图都是由边长为1的正三角形组成的，请以图中给出的图案为基本图形（其顶点均在格点上），在图2、图3中再分别添加若干个基本图形，使添加的图形与原基本图形组成一个新图案，要求：
①图2中设计的图案既是旋转对称图形又是轴对称图形；
②图3中设计的图案是旋转对称图形，但不是中心对称图形；
③所设计的图案顶点都在格点上，并给图案上阴影（建议用一组平行线段表示阴影）．
【答案】（1）正方形是旋转对称图形，最小旋转角为90°，正六边形是旋转对称图形，最小旋转角为60°；（2）①见解析；②见解析；③见解析
【分析】（1）利用旋转对称图形的性质分别得出符合题意的答案即可；
（2）①利用旋转对称图形以及轴对称图形的性质得出符合题意的答案即可；
②利用旋转对称图形性质得出符合题意的答案即可．
【详解】解：（1）正方形是旋转对称图形，最小旋转角为90°；正六边形是旋转对称图形，最小旋转角为60°；
（2）①如图2所示：
②如图3所示：
【点睛】此题考查了旋转对称图形和轴对称图形的性质，解题的关键是熟练掌握旋转对称图形和轴对称图形的性质．