2024内蒙古中考数学一轮知识点复习微专题辅助圆问题（课件）

展开

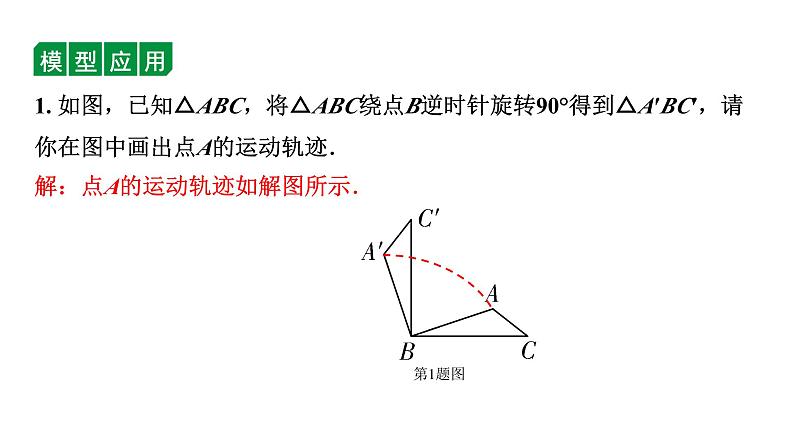
这是一份2024内蒙古中考数学一轮知识点复习微专题辅助圆问题（课件），共25页。PPT课件主要包含了第1题图，第2题图，第2题解图，第3题图，BD或BA或BC，模型二点圆最值，第4题图，第5题图，模型三线圆最值，第6题图等内容，欢迎下载使用。

1. 如图，已知△ABC，将△ABC绕点B逆时针旋转90°得到△A′BC′，请你在图中画出点A的运动轨迹．
解：点A的运动轨迹如解图所示．
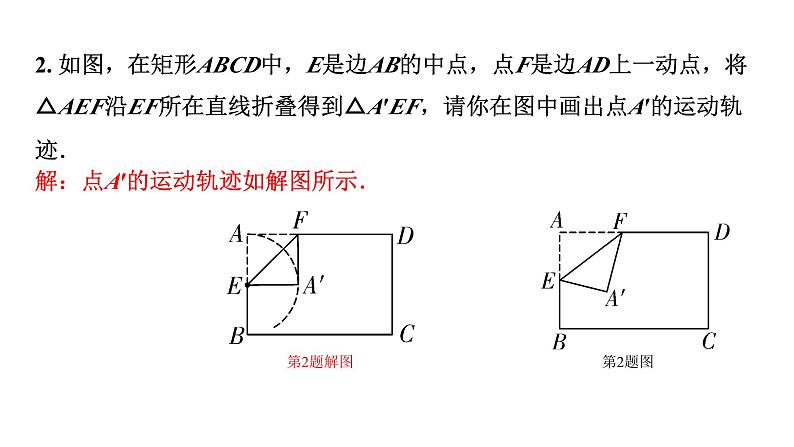
2. 如图，在矩形ABCD中，E是边AB的中点，点F是边AD上一动点，将△AEF沿EF所在直线折叠得到△A′EF，请你在图中画出点A′的运动轨迹．
解：点A′的运动轨迹如解图所示．
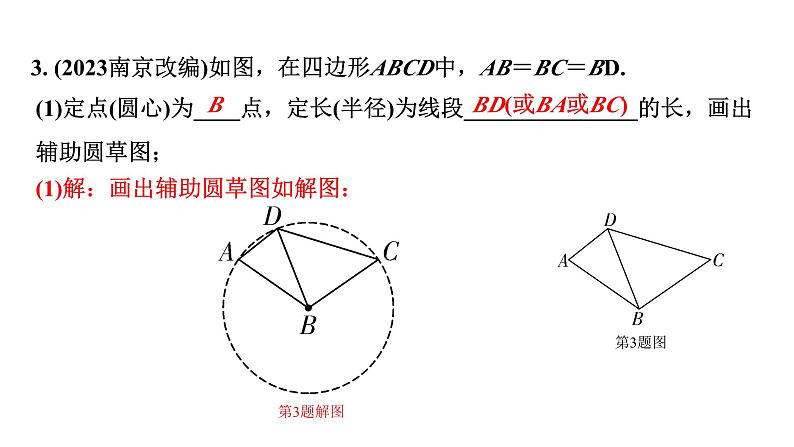
3. (2023南京改编)如图，在四边形ABCD中，AB＝BC＝BD.
(1)定点(圆心)为____点，定长(半径)为线段_______________的长，画出辅助圆草图；
(1)解：画出辅助圆草图如解图：
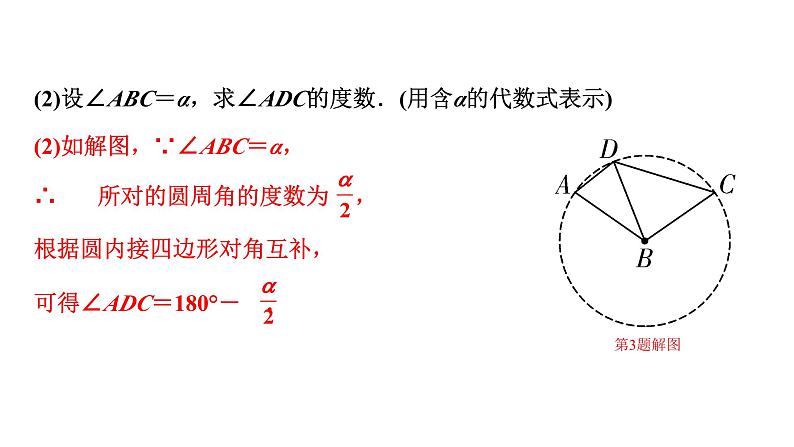
(2)设∠ABC＝α，求∠ADC的度数．(用含α的代数式表示)
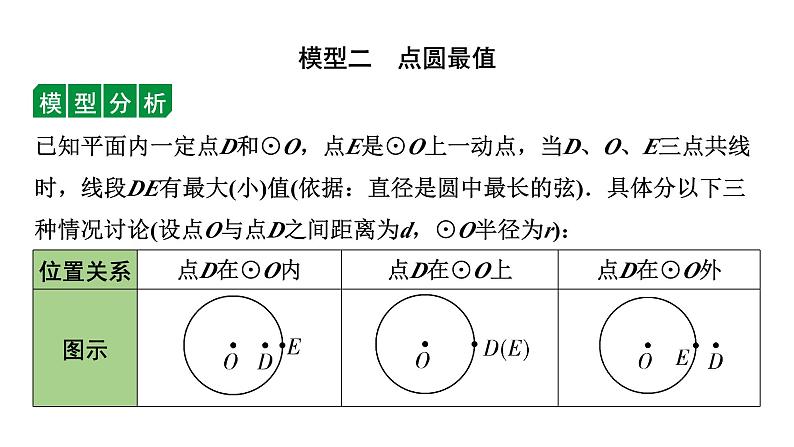
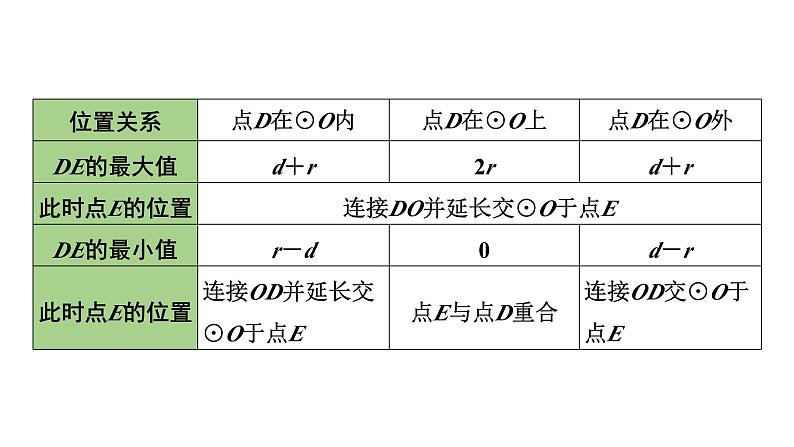
已知平面内一定点D和⊙O，点E是⊙O上一动点，当D、O、E三点共线时，线段DE有最大(小)值(依据：直径是圆中最长的弦)．具体分以下三种情况讨论(设点O与点D之间距离为d，⊙O半径为r)：
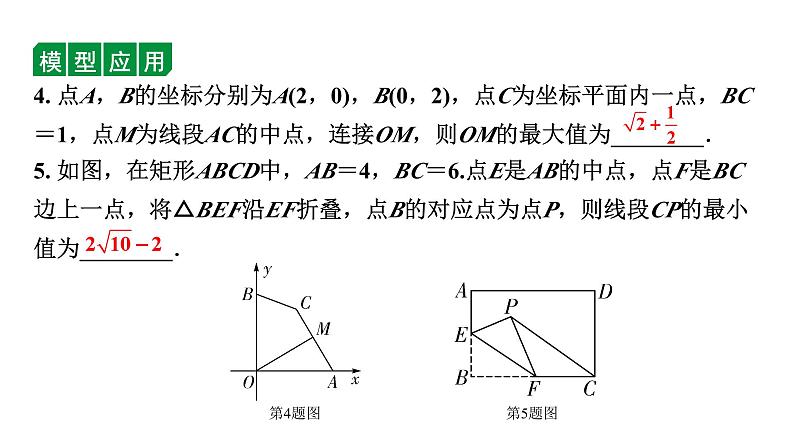
5. 如图，在矩形ABCD中，AB＝4，BC＝6.点E是AB的中点，点F是BC边上一点，将△BEF沿EF折叠，点B的对应点为点P，则线段CP的最小值为________．
4. 点A，B的坐标分别为A(2，0)，B(0，2)，点C为坐标平面内一点，BC＝1，点M为线段AC的中点，连接OM，则OM的最大值为________．
1. AB为⊙O的一条定弦，点C为AB一侧弧上一动点．(1)如图①，点C在优弧上，当CH⊥AB且CH过圆心O时，线段CH即为点C到弦AB的最大距离，此时S△ABC最大；(2)如图②，点C在劣弧上，当CH⊥AB且圆心O在CH的延长线上时，线段CH即为点C到弦AB的最大距离，此时S△ABC最大．
2. 如图，⊙O与直线l相离，点P是⊙O上的一个动点，设圆心O到直线l的距离为d，⊙O的半径为r，则点P到直线l的最小距离是d－r(如图③)，点P到直线l的最大距离是d＋r(如图④)．
推广：在解决某些面积最值问题时，常利用此模型，将问题转化为求动顶点到定边的最大(小)距离，从而利用面积公式求解．
6. 如图，已知∠BOA＝30°，M为OB边上一点，OM＝5，以M为圆心，2为半径作⊙M.则⊙M上的点到直线OA的最大距离为_____，最小距离为_____．
7. 如图，在Rt△ABC中，∠C＝90°，AC＝6，BC＝8，点F在边AC上，并且CF＝2，点E为边BC上的动点，将△CEF沿直线EF翻折，点C落在点P处，则点P到边AB距离的最小值是____．
8. (2023通辽)如图，AB是⊙O的弦，AB＝2 ，点C是⊙O上的一个动点，且∠ACB＝60°，若点M，N分别是AB，BC的中点，则图中阴影部分面积的最大值是_________．
模型引入：△ABC中，AB的长度为定值(定弦)，顶点C为动点(定弦的同一侧)，且∠C的度数为定值(定角)，我们把这样的模型根据其特征称为定弦对定角模型．模型探究：如图，点C为同一平面内线段AB外一动点，连接AC，BC，且∠ACB为定值，则点C的运动轨迹可分三种情况：
(1)如图①，当∠ACB＜90°时，点C的轨迹为优弧 (不包含A、B两点)；(2)如图②，当∠ACB＝90°时，点C的轨迹为以AB为直径的⊙O(不包含A、B两点)；
(3)如图③，当∠ACB＞90°时，点C的运动轨迹为劣弧 (不包含A、B两点)．
推广：在几何图形最值问题中，常通过定弦对定角模型来找动点的运动轨迹，解题时作出辅助圆是关键，然后结合求点圆、线圆最值等方法进行相关计算．
∠AOB＋∠ACB＝180°
9. 如图，已知AB＝6，∠ACB＝90°.
(1)定弦为_____，定角为________，画出辅助圆草图及面积最大时点C的位置；
以AB为直径构造辅助圆，如解图，当OC⊥AB时，△ABC的面积最大；
(2)△ABC的面积的最大值为____．
10. 如图，∠AOB＝45°，在边OA，OB上分别有两个动点C、D. 连接CD，以CD为直角边作等腰直角△CDE，已知CD＝2.
(1)定弦为______，定角为________，画出辅助圆草图及线段OE最大时点E的位置；
解：辅助圆草图及线段OE最大时点E的位置如解图：
(2)OE的最大值为________．
11. 如图，△ABC为等边三角形，AB＝2，点P为△ABC内一动点，且满足∠PAB＝∠ACP.
(1)定弦为_____，定角为________，画出辅助圆草图及线段PB最小时点P的位置；
解：辅助圆草图及线段PB最小时点P的位置如解图；
(2)线段PB的最小值为________．