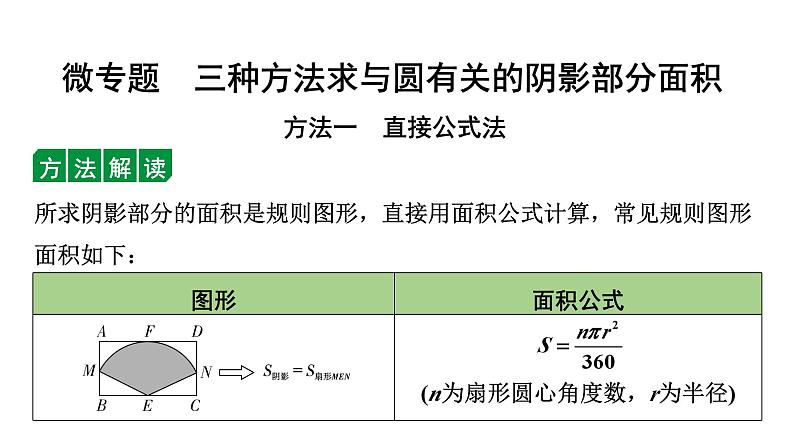
2024内蒙古中考数学一轮知识点复习 微专题 三种方法求与圆有关的阴影部分面积（课件）

这是一份2024内蒙古中考数学一轮知识点复习 微专题 三种方法求与圆有关的阴影部分面积（课件），共16页。PPT课件主要包含了第1题图，第2题图，方法二和差法，直接和差法，第3题图，第4题图，构造和差法，第5题图，第6题图，方法三转化法等内容，欢迎下载使用。

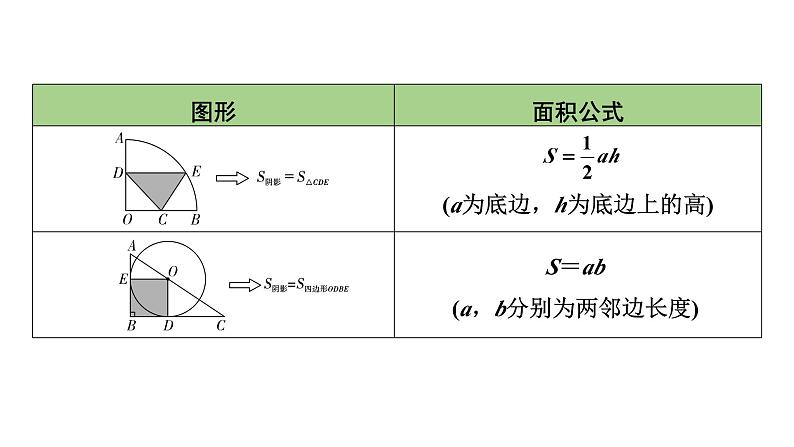
S＝ab(a，b分别为两邻边长度)
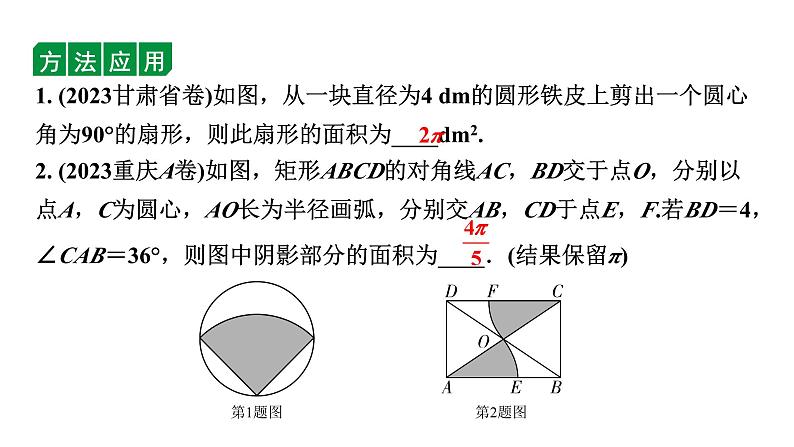
1. (2023甘肃省卷)如图，从一块直径为4 dm的圆形铁皮上剪出一个圆心角为90°的扇形，则此扇形的面积为____dm2.
2. (2023重庆A卷)如图，矩形ABCD的对角线AC，BD交于点O，分别以点A，C为圆心，AO长为半径画弧，分别交AB，CD于点E，F.若BD＝4，∠CAB＝36°，则图中阴影部分的面积为____．(结果保留π)
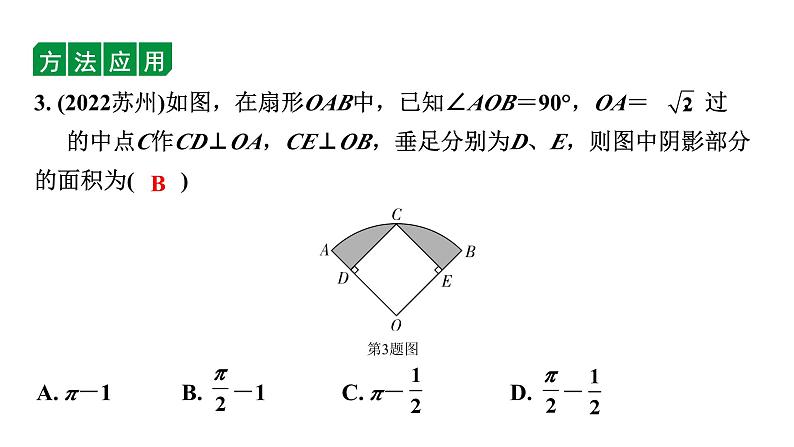
3. (2022苏州)如图，在扇形OAB中，已知∠AOB＝90°，OA＝ ，过 的中点C作CD⊥OA，CE⊥OB，垂足分别为D、E，则图中阴影部分的面积为(　　)
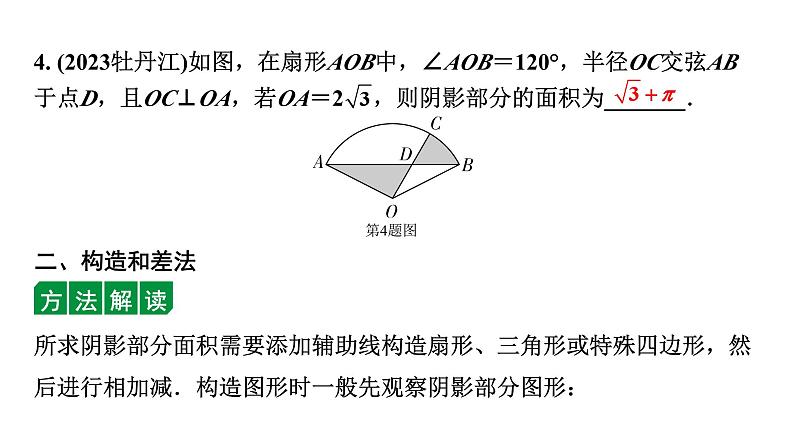
4. (2023牡丹江)如图，在扇形AOB中，∠AOB＝120°，半径OC交弦AB于点D，且OC⊥OA，若OA＝2 ，则阴影部分的面积为_______．
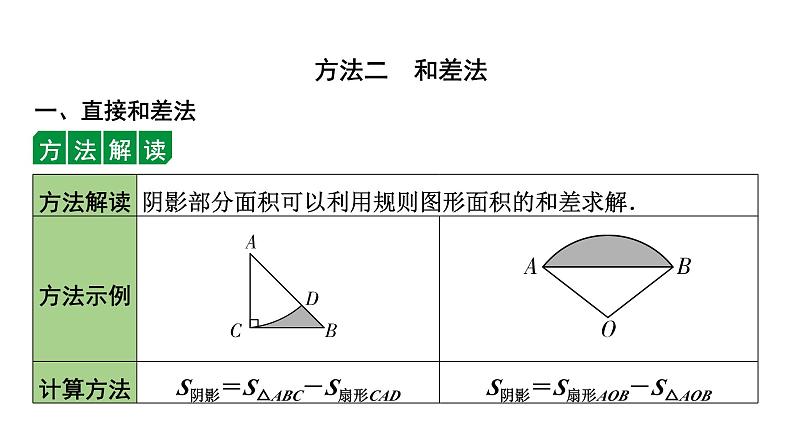
所求阴影部分面积需要添加辅助线构造扇形、三角形或特殊四边形，然后进行相加减．构造图形时一般先观察阴影部分图形：
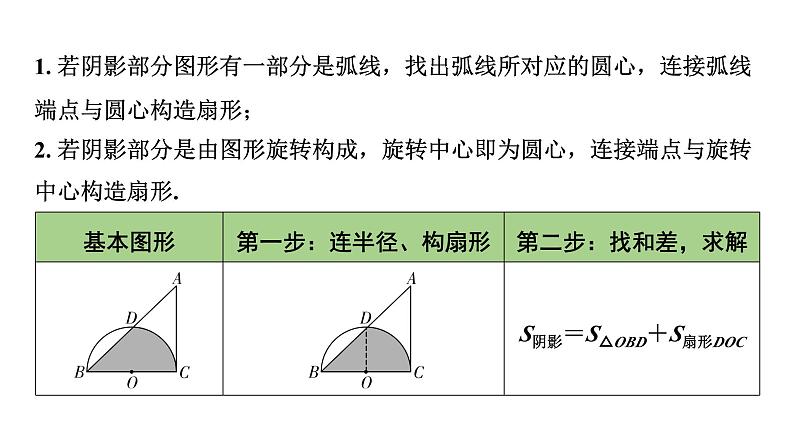
1. 若阴影部分图形有一部分是弧线，找出弧线所对应的圆心，连接弧线端点与圆心构造扇形；2. 若阴影部分是由图形旋转构成，旋转中心即为圆心，连接端点与旋转中心构造扇形.
5. 如图，点A，B，C，D在⊙O上，AB＝AC，∠A＝40°，BD∥AC，若⊙O的半径为2.则图中阴影部分的面积是(　　)
A. B. C. D.
6. 如图，在扇形AOB中，∠AOB＝90°，OA＝4，以OB为直径作半圆，圆心为点C，过点C作OA的平行线分别交两弧于点D、E，则阴影部分的面积为________．
所求阴影部分面积无法直接计算时，可通过平移、旋转、对称等方法，将所求阴影部分面积转化为规则图形的面积或规则图形面积的和差.
S阴影＝S正方形BCFE
点D为 的中点
S阴影＝S扇形ACB－S△ADC
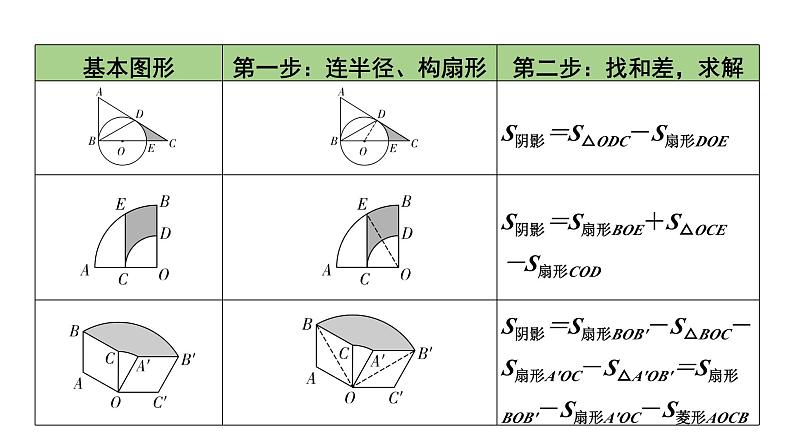
S阴影＝S扇形ABE－S扇形MBN
如图，△ABC内接于⊙O，AB是⊙O的直径，若∠BAC＝
35°，AB＝6，则阴影部分的面积为(　　)
A. B. π C. D. 2π
8. (2023枣庄)如图，正方形ABCD的边长为2，O为对角线的交点，点E、F分别为BC、AD的中点．以C为圆心，2为半径作圆弧 ，再分别以E、F为圆心，1为半径作圆弧 、 ，则图中阴影部分的面积为(　　)
A. π－1 B. π－3 C. π－2 D. 4－π