甘肃省武威市古浪县裴家营学校联片教研2023-2024学年八年级下学期7月期末考试数学试题

这是一份甘肃省武威市古浪县裴家营学校联片教研2023-2024学年八年级下学期7月期末考试数学试题，共8页。
一．选择题（共30分）
1．（3分）若式子有意义，则x的取值范围是（ ）
A．x≤3B．x≥﹣3C．x≠3D．x≥0
2．（3分）若x＝1﹣，则代数式x2﹣2x+1的值是（ ）
A．2021B．2022C．﹣2021D．﹣2022
3．（3分）如图所示，△ABC中，CD⊥AB于D，若AD＝2BD，AC＝3，BC＝2，则BD的长为（ ）
A．B．C．1D．
4．（3分）下列长度的三条线段能组成直角三角形的是（ ）
A．3，4，5B．10，15，20C．1，，3D．2，3，4
5．（3分）如图，四边形ABCD的对角线AC和BD相交于点O，下列不能判定四边形ABCD为平行四边形的条件是（ ）
A．OA＝OC，OB＝OD B．OA＝OC，AB∥DC
C．∠ABD＝∠ADB，∠BAO＝∠DCO D．AB＝DC，AD＝BC
6．（3分）如图，四边形ABCD为菱形，AB＝4，∠A＝60°，则BD的长为（ ）
A．2B．4C．D．
7．（3分）如图①，在正方形ABCD中，点E为DC边的中点，点P为线段BE上的一个动点．设BP＝x，AP＝y，图②是点P运动时y随x变化的关系图象．当y＝2时，则（ ）
A．P在B点处B．P在E点处C．AP⊥BED．P为BE中点
8．（3分）若直线y＝2x+b经过点A（﹣2，m），B（1，n），则m，n的大小关系正确的是（ ）
A．m＜nB．m＞nC．m＝nD．无法确定
9．（3分）某学校规定本学期学生的数学成绩是把期末成绩、期中成绩和平时作业成绩按如图所示的比例计算．已知小明的期末成绩为90分，期中成绩为85分，平时作业成绩为80分，则本学期小明的数学成绩为（ ）
A．85分B．86分C．87分D．88分
10．（3分）已知一组数据3、6、x、5、5、7的平均数是5，则这组数据的方差是（ ）
A．1B．C．2D．
二．填空题（共24分）
11．（3分）计算：2×÷＝ ．
12．（3分）若最简二次根式与是同类二次根式，则a＝ ．
13．（3分）已知等腰三角形的两边分别为6和4，则这个等腰三角形的面积为 ．
14．（3分）若如图所示的网格是正方形网格，则∠ABC+∠ACB＝ ．（点A，B，C在网格格点上）
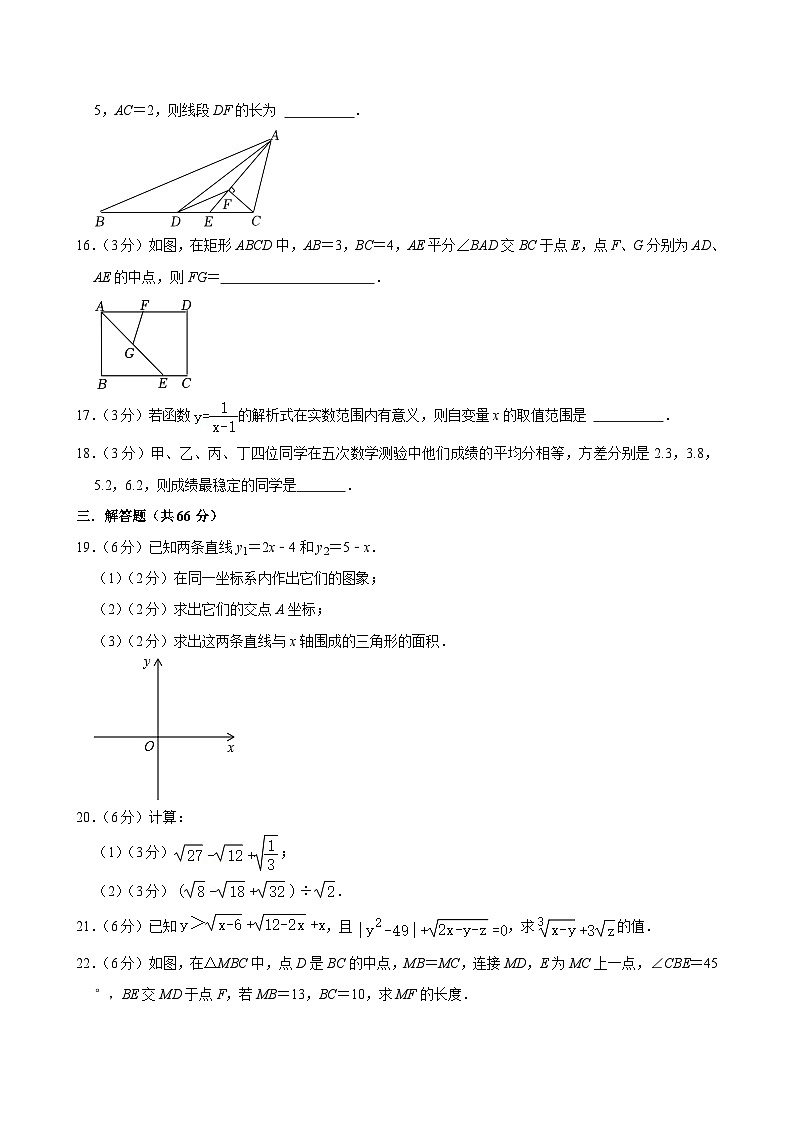
15．（3分）如图，在△ABC中，AD是BC边上的中线，AE是∠BAC的平分线，CF⊥AE于F．若AB＝5，AC＝2，则线段DF的长为 ．
16．（3分）如图，在矩形ABCD中，AB＝3，BC＝4，AE平分∠BAD交BC于点E，点F、G分别为AD、AE的中点，则FG＝ ．
17．（3分）若函数的解析式在实数范围内有意义，则自变量x的取值范围是 ．
18．（3分）甲、乙、丙、丁四位同学在五次数学测验中他们成绩的平均分相等，方差分别是2.3，3.8，5.2，6.2，则成绩最稳定的同学是 ．
三．解答题（共66分）
19．（6分）已知两条直线y1＝2x﹣4和y2＝5﹣x．
（1）（2分）在同一坐标系内作出它们的图象；
（2）（2分）求出它们的交点A坐标；
（3）（2分）求出这两条直线与x轴围成的三角形的面积．
20．（6分）计算：
（1）（3分）；
（2）（3分）．
21．（6分）已知，且，求的值．
22．（6分）如图，在△MBC中，点D是BC的中点，MB＝MC，连接MD，E为MC上一点，∠CBE＝45°，BE交MD于点F，若MB＝13，BC＝10，求MF的长度．
23．（6分）在△ABC中，∠C＝90°，BC：AB＝3：5且AB＝20cm，求边AC的长度．
24．（6分）如图，在Rt△ABC中，∠BAC＝90°，E、F分别是BC、AC的中点，延长BA到点D，使AD＝AB，连结DE、DF．
（1）（3分）求证：AF与DE互相平分；
（2）（3分）若BC＝5，求DF的长．
25．（6分）如图，在矩形ABCD中，对角线BD的垂直平分线MN与AD相交于点M，与BD相交于点O，与BC相交于点N，连接BM、DN．
（1）（3分）求证：四边形BMDN是菱形；
（2）（3分）若AB＝4，AD＝8，求菱形BMDN的面积．
26．（6分）在“世界读书日”前夕，某校开展了“让阅读滋养心灵”的读书活动．为了解该校学生在此次活动中的课外阅读情况，从中随机抽取50名学生，调查他们课外阅读书籍的数量，将收集的数据整理成如图所示统计图．
（1）（3分）求这组数据的平均数；
（2）（3分）该校共有800名学生，估计该校全体学生在这次活动中课外阅读书籍的总量大约是多少本？
27．（8分）如图，在△ABC中，∠ACB＝90°，点D是边AB的中点，连接CD，过点C作CE∥AB，过点B作BE∥CD，CE，BE交于点E．
（1）（4分）判断四边形CDBE是什么特殊的四边形，并证明；
（2）（4分）直接写出当△ABC再满足什么条件时，四边形CDBE是正方形．
28．（10分）如图，在平面直角坐标系中，直线AB分别与x轴的负半轴、y轴的正半轴交于A、B两点，其中OA＝2，S△ABC＝12，点C在x轴的正半轴上，且OC＝OB．
（1）（3分）求直线AB的解析式；
（2）（3分）将直线AB向下平移6个单位长度得到直线l1，直线l1与y轴交于点E，与直线CB交于点D，过点E作y轴的垂线l2，若点P为y轴上一个动点，Q为直线l2上一个动点，求PD+PQ+DQ的最小值；
（3）（4分）若点M为直线AB上的一点，在y轴上是否存在点N，使以点A、D、M、N为顶点的四边形为平行四边形，若存在，请直接写出点N的坐标；若不存在，请说明理由．
答案
1-5 ABBAC 6-10 BCACB
11．1． 12．4． 13．3或8． 14．45°． 15．1.5
16．． 17．x≠1． 18．甲．
19．（1）
（2）A（3，2）
（3）
20．（1）；（2）3．
21．﹣1+．
22．7．
23．16cm．
24．（1）连接EF，AE．
∵点E，F分别为BC，AC的中点，
∴EF∥AB，EF＝AB．
又∵AD＝AB，
∴EF＝AD．
又∵EF∥AD，
∴四边形AEFD是平行四边形．
∴AF与DE互相平分．
（2）在Rt△ABC中，
∵E为BC的中点，BC＝5，
∴AE＝BC＝．
又∵四边形AEFD是平行四边形，
∴DF＝AE＝．
25．（1）∵四边形ABCD是矩形，
∴AD∥CB，
∴∠ODM＝∠OBN，
∵MN垂直平分BD，
∴OD＝OB，
在△ODM和△OBN中，
，
∴△ODM≌△OBN（ASA），
∴DM＝BN，
∵DM＝BM，DN＝BN，
∴DM＝BM＝DN＝BN，
∴四边形BMDN是菱形．
（2）∵∠D＝90°，AB＝4，AD＝8，
∴AB2+AM2＝BM2，AM＝8﹣DM，
∵DM＝BM，
∴42+（8﹣DM）2＝DM2，
解得DM＝5，
∵AB⊥DM，
∴S菱形BMDN＝DM•AB＝5×4＝20，
∴菱形BMDN的面积为20．
26．（1）2.3本；（2）1840本．
27．（1）四边形CDBE是菱形，
证明：∵BE∥CD，CE∥AB，
∴四边形BDCE是平行四边形．
∵∠ACB＝90°，CD是AB边上的中线，
∴CD＝BD，
∴平行四边形BDCE是菱形；
（2）当△ABC是等腰直角三角形时，四边形CDBE是正方形；理由如下：
∵∠ACB＝90°，
当△ABC是等腰直角三角形，
∵D为AB的中点，
∴CD⊥AB，
∴∠CDB＝90°，
∴四边形BECD是正方形．
28．（1）y＝2x+4；
（2）4；
（3）（0，﹣2）或（0，10）．