甘肃省武威市凉州区武威二十一中联片教研2023-2024学年八年级下学期7月期末数学试题

这是一份甘肃省武威市凉州区武威二十一中联片教研2023-2024学年八年级下学期7月期末数学试题，共9页。
一．选择题（共30分）
1．（3分）已知a是正整数，是整数，则a的最小值是（ ）
A．3B．4C．5D．6
2．（3分）下列运算正确的是（ ）
A．B．C．D．
3．（3分）如图，在Rt△ABC中，∠C＝90°，∠B＝30°，BC＝6，AD平分∠CAB交BC于点D，点E为边AB上一点，则线段DE长度的最小值为（ ）
A．B．C．2D．3
4．（3分）如图所示的网格是正方形网格，点A，B，C，P是网格线交点，且点P在△ABC的边AC上，则∠PAB+∠PBA＝（ ）
A．45°B．30°C．60°D．90°
5．（3分）如图，点E为▱ABCD的对角线AC上一点，AC＝5，CE＝1，连接DE并延长至点F，使得EF＝DE，连接BF，则BF为（ ）
A．B．3C．D．4
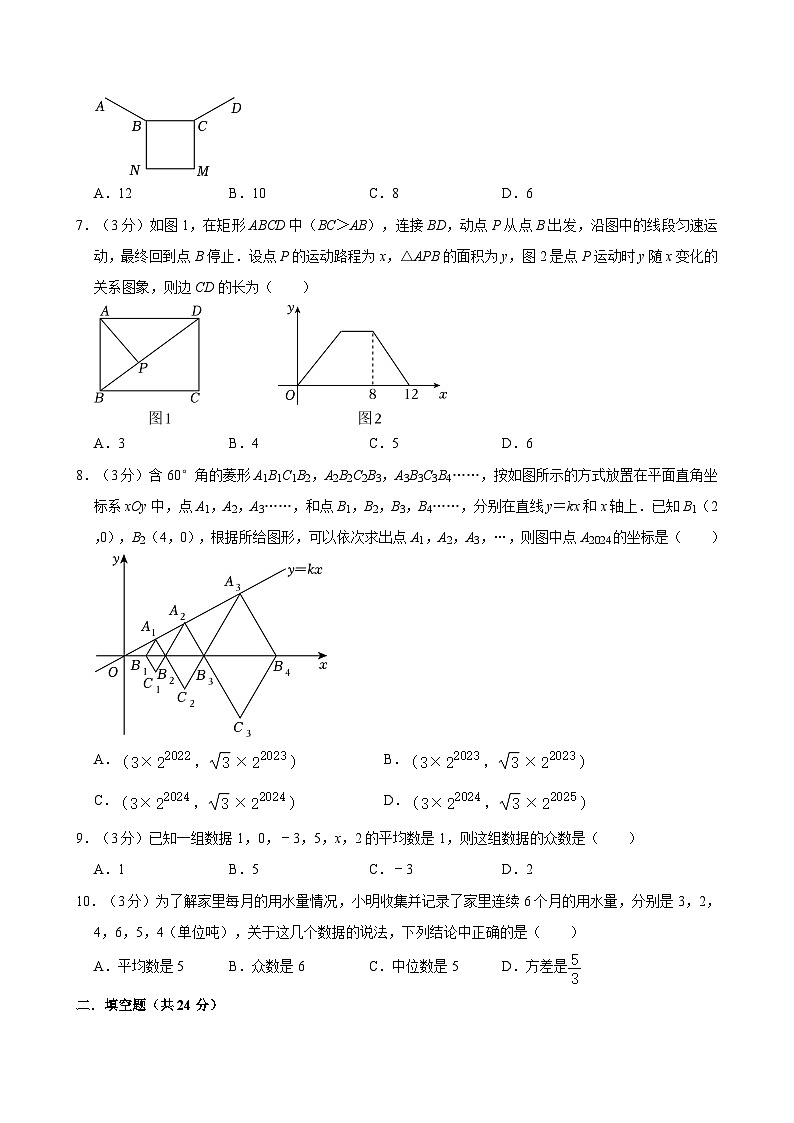
6．（3分）如图，已知AB，BC，CD是正n边形的三条边，在同一平面内，以BC为边在该正n边形的外部作正方形BCMN．若∠ABN＝120°，则n的值为（ ）
A．12B．10C．8D．6
7．（3分）如图1，在矩形ABCD中（BC＞AB），连接BD，动点P从点B出发，沿图中的线段匀速运动，最终回到点B停止．设点P的运动路程为x，△APB的面积为y，图2是点P运动时y随x变化的关系图象，则边CD的长为（ ）
A．3B．4C．5D．6
8．（3分）含60°角的菱形A1B1C1B2，A2B2C2B3，A3B3C3B4……，按如图所示的方式放置在平面直角坐标系xOy中，点A1，A2，A3……，和点B1，B2，B3，B4……，分别在直线y＝kx和x轴上．已知B1（2，0），B2（4，0），根据所给图形，可以依次求出点A1，A2，A3，…，则图中点A2024的坐标是（ ）
A． B．
C． D．
9．（3分）已知一组数据1，0，﹣3，5，x，2的平均数是1，则这组数据的众数是（ ）
A．1B．5C．﹣3D．2
10．（3分）为了解家里每月的用水量情况，小明收集并记录了家里连续6个月的用水量，分别是3，2，4，6，5，4（单位吨），关于这几个数据的说法，下列结论中正确的是（ ）
A．平均数是5B．众数是6C．中位数是5D．方差是
二．填空题（共24分）
11．（3分）要使代数式有意义，则x的取值范围是 ．
12．（3分）化简：＝ ．
13．（3分）如图，在Rt△ABC中，∠ACB＝90°，CD⊥AB于点D，BC＝8，AB＝17，点P是Rt△ABC的直角边的中点，连接PD，则线段PD的长为 ．
14．（3分）如图，平行四边形ABCD的对角线AC，BD相交于点O，点E为AB中点，AE＝3，EO＝2，则平行四边形ABCD的周长为 ．
15．（3分）如图，在平行四边形ABCD中，AB＝8，BC＝12，∠B＝120°，E是BC的中点，点P在平行四边形ABCD的边上，若△PBE为等腰三角形，则EP的长为 ．
16．（3分）如图，A、B两点的坐标分别为（5，0）、（6，3），C是平面直角坐标系内一点．若四边形OABC是平行四边形，则点C的坐标为 ．
17．（3分）已知A（﹣1，y1），B（﹣0.5，y2），C（1.7，y3），是直线y＝﹣9x+b（b为常数）上的三个点，则y1，y2，y3中最小的是 ．
18．（3分）若一组数据6，6，m，7，7，8的众数为7，则这组数据的中位数为 ．
三．解答题（共66分）
19．（4分）计算：．
20．（6分）已知x，y都是实数，且，求以实数x，y为两边的直角三角形的第三边m的长．
21．（6分）在边长为1的正方形网格中，△ABC的三个顶点均在格点上，请按要求完成下列各题：
（1）（3分）△ABC的面积为 ；
（2）（3分）试说明：∠BAC＝90°．
22．（8分）如图，在▱ABCD中，E，F是对角线BD上的点，且DE＝BF．求证：∠1＝∠2．
23．（8分）如图，在▱ABCD中，E，F分别是边AD，BC的中点，且AC平分∠DAF．连结AF，CE，AC．
（1）（4分）判断四边形AFCE的形状，并说明理由．
（2）（4分）若AB＝AF＝3，求AC的长度．
24．（8分）已知函数．
（1）（4分）请在所给的平面直角坐标系中画出该函数的图象．
（2）（4分）结合所画图象，分别求出在函数图象上满足下列条件的点的坐标．
①横坐标是﹣4； ②和x轴的距离是2个单位长度．
25．（8分）某校举办“十佳歌手”演唱比赛，五位评委进行现场打分，将甲、乙、丙三位选手得分数据整理成下列统计图．
（1）（2分）完成表格：
（2）（3分）从三位选手中选一位参加市级比赛，你认为选谁更合适，请说明理由；
（3）（3分）在演唱比赛中，往往在所有评委给出的分数中，去掉一个最高分和一个最低分，然后计算余下分数的平均分．如果去掉一个最高分和一个最低分之后甲的方差记为s2，则s2 0.56．
26．（8分）如图1，过点B（4，4）作BA⊥x轴于点A，作BC⊥y轴于点C，连接OB，点D是线段OB上的一点，连接CD，过点D作DE⊥DC，交x轴于点E，点F在射线CB上，且DC＝DF，连接AD，设点D坐标为（m，n）．
（1）（2分）若点D的坐标为（3，3），求DF所在直线的解析式；
（2）（3分）求S△ADE；
（3）（3分）如图2，延长CD与直线AB交于点G，当△ADG为等腰三角形时，求点G坐标．
27．（10分）在平面直角坐标系xOy中，对于任意两个图形T和图形W，给出如下定义：M，N分别为图形T和图形W上任意一点，将M，N两点间距离的最小值称为图形T和图形W之间的“关联距离”，记作d（T，W）．如图，已知△ABC，其中A（﹣2，3），B（﹣2，﹣1），C（1，3），D，E为三角形外两点．例如，点A与x轴之间的“关联距离”d（A，x轴）＝3，线段AB与y轴之间的“关联距离”d（AB，y轴）＝2．
（1）（3分）求点A与直线BC之间的“关联距离”d（A，直线BC）；
（2）（3分）若D（3，1），E（5，1），将线段DE向左平移n个单位，当线段DE与△ABC之间的“关联距离”d（DE，△ABC）＝0时，求n的最小值；
（3）（4分）若D（m，﹣2），E（m+2，﹣4），当﹣2≤m≤3时，对于每一个m，都满足线段DE与一次函数y＝kx﹣2k（k是常数，k≠0）的图象之间的“关联距离”d（DE，直线y＝kx﹣2k）＞0，求k的取值范围．
答案
1-5 DCCAB 6-10 AABAD
11．x≥﹣1．12．3．13．4或．14．20．15．6或6或．16．（1，3）．17．y3．18．7．
19．﹣． 20．第三边m的长为5或．
21．（1）5；（2）∵，，
又∵，
∴△ABC是直角三角形，
∴∠BAC＝90°．
22．∵四边形ABCD是平行四边形，
∴AD＝BC，AD∥BC，
∴∠ADE＝∠CBF．
在△ADE和△CBF中，
，
∴△ADE≌△CBF（SAS），
∴∠1＝∠2．
23．（1）四边形AFCE是菱形，
理由：∵四边形ABCD是平行四边形，
∴AD∥BC，AD＝BC，
∴AD＝BC，
∵E，F分别是边AD，BC的中点，
∴AE＝AD，CF＝BC，
∴AE∥CF，且AE＝CF，
∴四边形AFCE是平行四边形，
∵AC平分∠DAF，
∴∠DAC＝∠FAC，
∵∠DAC＝∠FCA，
∴∠FAC＝∠FCA，
∴AF＝CF，
∴四边形AFCE是菱形．
（2）∵AB＝AF＝3，AF＝CF＝BF，
∴AB＝AF＝CF＝BF＝3，
∴△ABC是等边三角形，BC＝2BF＝6，∠FAC＝∠FCA，
∴∠B＝∠AFB＝∠BAF＝60°，
∵∠B＝∠FAC+∠FCA＝2∠FAC＝60°，
∴∠FAC＝30°，
∴∠BAC＝∠BAF+∠FAC＝60°+30°＝90°，
∴AC＝＝＝3，
∴AC的长是3．
24．（1）当x＝0时，y＝3；
当x＝2时，y＝2；
函数图象如图所示，
（2）①由函数图象可知，
当x＝﹣4时，y＝5；
故函数图象上横坐标是﹣4的点坐标为（﹣4，5）．
②和x轴的距离是2个单位长度的点的纵坐标为2或﹣2，
当y＝2时，x＝2；
当y＝﹣2时，x＝10；
所以函数图象上和x轴的距离是2个单位长度的点的坐标为（2，2）或（10，﹣2）．
25．（1）①9；②8.8；（2）选甲，方差最小最稳定；（3）＜．
26．（1）y＝x+2；（2）S△ADE＝﹣m2+4m；
（3）点G的坐标为4，4﹣）或（4，4﹣4）．
27．（1）d（A，直线BC）＝；
（2）n的最小值为3；
（3）d（DE，直线y＝kx﹣2k）＞0．
声明：试题解析著作权属所有，未经书面同意，不得复制发布日期：2024/6/17 17:24:00；用户：体验；邮箱：xn1312@xyh.cm；学号：55982971平均数/分
中位数/分
方差/分2
甲
8.8
①
0.56
乙
8.8
9
0.96
丙
②
8
0.96