数学七年级下册8.3 同底数幂的除法获奖ppt课件

这是一份数学七年级下册8.3 同底数幂的除法获奖ppt课件，文件包含苏科版本数学七年级下册83《同底数幂的除法》第1课时课件pptx、苏科版本数学七年级下册83《同底数幂的除法》第2课时课件pptx、苏科版本数学七年级下册83《同底数幂的除法》重难点专项练习九大题型原卷版docx、苏科版本数学七年级下册83《同底数幂的除法》重难点专项练习九大题型解析版docx等4份课件配套教学资源，其中PPT共52页， 欢迎下载使用。

能根据指数与幂的关系，推导出负整数指数幂的运算法则，并重新定义同底数幂的除法法则
掌握负整数指数幂的运算法则，并熟练运用于计算
重新定义科学计数法，能用科学计算法表示较小的数
牢记幂的全部运算法则，并熟练运用于混合计算
如果可以，23÷24=23-4=2-1，2-1是什么？等于几？
【操作层面总结】底数取倒数指数去负号
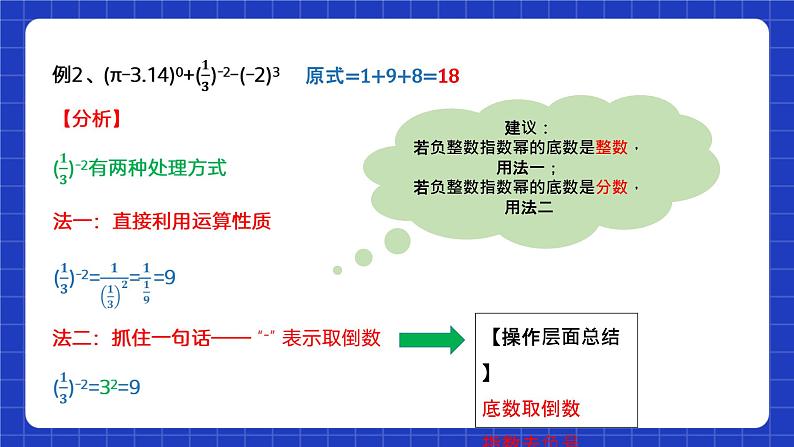
原式=1+9+8=18
建议：若负整数指数幂的底数是整数，用法一；若负整数指数幂的底数是分数，用法二
(-10)5=-100000
同底数幂除法的运算性质可以进阶啦~
Q2：完成下列计算，并交流讨论各自的计算方式（1）a5÷a0（a≠0）;（2）a5÷a-2（a≠0）
法二：运用“同底数幂除法”的运算性质（1）a5÷a0=a5-0=a5（2）a5÷a-2=a5-(-2)=a7
例3、完成下列计算，并交流讨论各自的计算方式（1）a5÷a0（a≠0）;（2）a5÷a-2（a≠0）
Q1：太阳的半径约为700000000m；太阳的主要成分是氢，氢原子的半径约为0.00000000005m。这两个数据能否都用科学计数法表示？
【分析】700000000=7×108
【科学记数法】一般地，用科学记数法可以把一个正数写成a×10n的形式，其中1≤a<10，n是整数
有了负整数指数幂，较小的数也可以用科学记数法表示，科学记数法的概念就可以进阶啦~
【原始版】一般地，一个大于10的数可以写成a×10n的形式，其中1≤a<10，n是正整数
例4、中芯国际集成电路制造有限公司，是世界领先的集成电路晶圆代工企业之一，也是中国内地技术最先进、配套最完善、规模最大、跨国经营的集成电路制造企业集团，中芯国际第一代14纳米FinFET技术取得了突破性进展，并于2019年第四季度进入量产，代表了中国大陆自主研发集成电路的最先进水平，14纳米=0.000000014米，0.000000014用科学记数法表示为____________________．
【分析】0.000000014=1.4×10-8
【科学记数法——表示较小的数】
如何快速确认负指数？法一：数小数点移动的位数法二：原数左边起第一个不为零的数字前面的0的个数
例5、新型冠状病毒的直径约为0.000000907米，0.000000907用科学记数法表示为____________________．
【分析】0.000000907=9.07×10-7
例6、已知一种细胞的直径约为2.13×10-4cm，请问2.13×10-4这个数原来的数是（　　）A．21300B．2130000C．0.0213D．0.000213
【分析】2.13×10-4=0.00213
【科学记数法——求原数】
小数点向左移4个单位即可
记忆技巧：降级运算的感觉~
例7、下列计算正确的是（　　）A．a3•a4=a12B．(ab2)3=ab6C．a10÷a2=a5D．(-a4)2=a8
【分析】A．a3•a4=a7，故本选项错误；B．(ab2)3=a3b6，故本选项错误；C．a10÷a2=a8，故本选项错误；D．(-a4)2=a8，故本选项正确．
【分析】（1）原式=-a3•a4-a6+a6=-a7
（2）原式=1-4+33=-3+27=24
例9、已知常数a，b满足2a×22b=8，且(5a)2×(52b)2÷(53a)b=1，求ab的值．
【分析】∵2a×22b=8，∴2a+2b=23，即a+2b=3，∵(5a)2×(52b)2÷(53a)b=1，∴52a×54b÷53ab=1，即52a+4b-3ab=50，∴2a+4b-3ab=0，∴2(a+2b)-3ab=0，即2×3-3ab=0，解得：ab=2．
【分析】（1）∵x3=m，x5=n，∴x14=x9•x5=(x3)3•x5=m3n；