苏科版七年级下册第9章 整式乘法与因式分解9.4 乘法公式优质ppt课件

这是一份苏科版七年级下册第9章 整式乘法与因式分解9.4 乘法公式优质ppt课件，文件包含苏科版本数学七年级下册94《乘法公式》第1课时课件pptx、苏科版本数学七年级下册94《乘法公式》第2课时课件pptx、苏科版本数学七年级下册94《乘法公式》重难点专项练习八大题型原卷版docx、苏科版本数学七年级下册94《乘法公式》重难点专项练习八大题型解析版docx等4份课件配套教学资源，其中PPT共61页， 欢迎下载使用。
理解完全平方公式的几何背景及两个公式的推导过程
能借助口诀牢记两个公式，并熟练运用两个公式进行计算与巧算
熟悉两个公式的变形式，并用以简化运算
理解完全平方式的概念，能对完全平方式进行判断
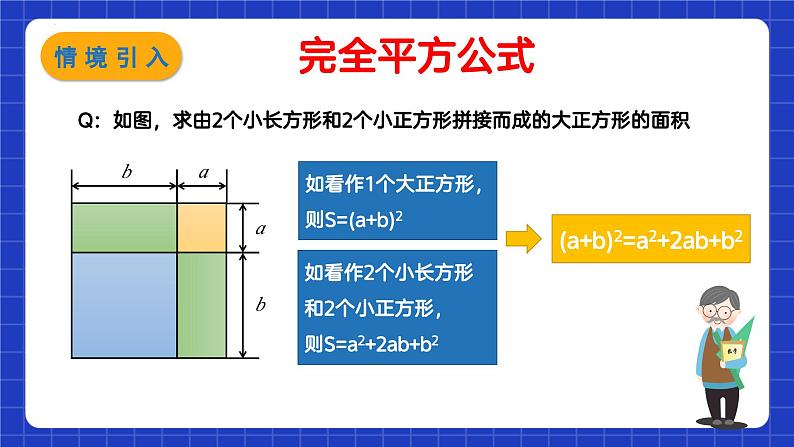
Q：如图，求由2个小长方形和2个小正方形拼接而成的大正方形的面积
如看作1个大正方形，则S=(a+b)2
如看作2个小长方形和2个小正方形，则S=a2+2ab+b2
(a+b)2=a2+2ab+b2
则：(a+b)2=(a+b)(a+b)=a2+ab+ab+b2=a2+2ab+b2
即：(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2
把a-b看作a+(-b)，则可以用(a+b)2=a2+2ab+b2这个公式
(a + b)2=a2+2ab+b2
[a + (-b)]2=a2+2·a·(-b)+(-b)2
【完全平方公式】(a+b)2=a2+2ab+b2(a-b)2=a2-2ab+b2
记忆口诀：首平方，末平方，积的两倍在中央（符号随中央）
【特征】①左边是两个数的和（或差）的平方；②右边是一个三项式，其中首末两项分别是两数的平方，都为正，中间一项是两数积的2倍，其符号与左边的运算符号相同．
计算：（1）(xy-4)2； （2）(2a+7b)2
【解答】（1）原式=(xy)2-2·(xy)·4+42=x2y2-8xy+16
把xy看作整体，则可以用完全平方公式
把2a、7b分别看作整体，则可以用完全平方公式
【解答】（2）原式=(2a)2+2·(2a)·(7b)+(7b)2=4a2+28ab+49b2
【注意点】①公式中的a、b可是具体数，也可以是单项式或多项式；②对形如两数和（或差）的平方的计算，都可以用这个公式．
计算：(a+b+c)2
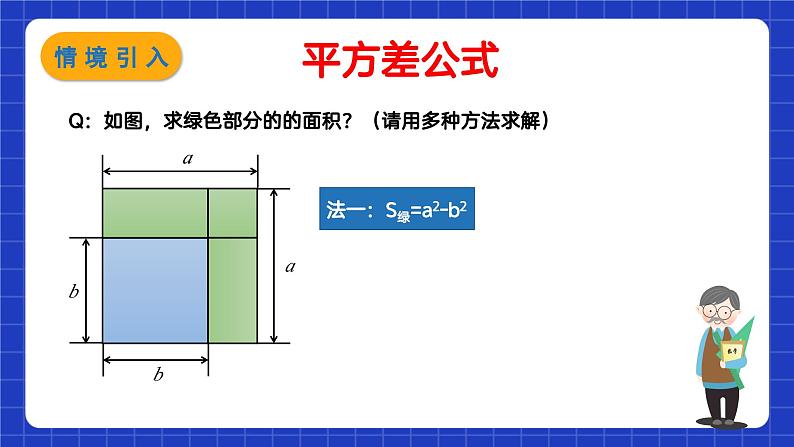
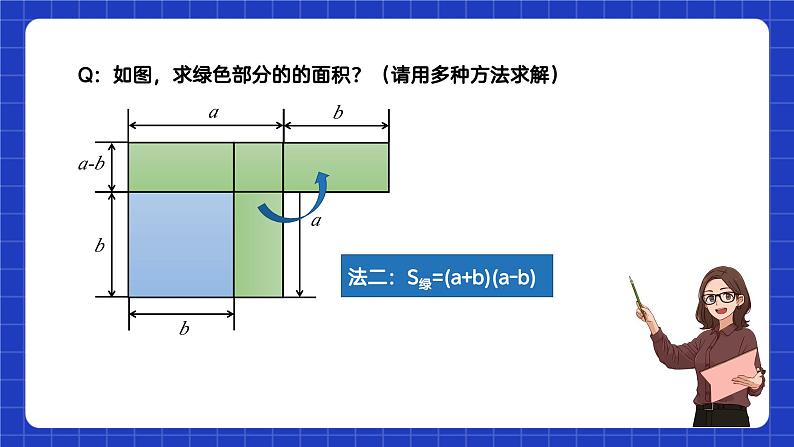
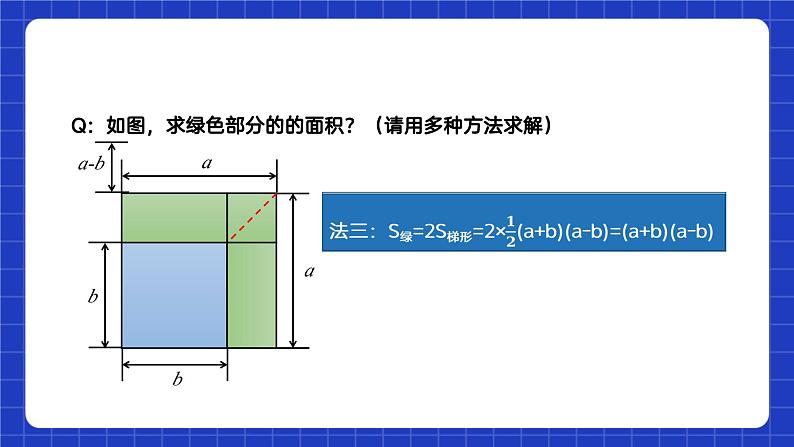
法一：用几何法大正方形的面积即(a+b+c)2=3个小正方形与6个长方形的面积之和=a2+b2+c2+2ab+2bc+2ca
【解答】法二：用多项式的乘法法则原式=(a+b+c)(a+b+c)=a2+ab+ac+ba+b2+bc+ca+cb+c2=a2+b2+c2+2ab+2bc+2ca
【解答】法三：用完全平方公式原式=[(a+b)+c]2=(a+b)2+2·(a+b)·c+c2=a2+2ab+b2+2ac+2bc+c2=a2+b2+c2+2ab+2bc+2ca
把(a+b)看作整体，则可以用完全平方公式
【拓展公式】(a+b+c)2=a2+b2+c2+2ab+2bc+2ca
【注意点】①公式中的a、b可是具体数，也可以是单项式或多项式；②对形如两数和（或差）的平方的计算，都可以用这个公式；③对于三项的可以把其中的两项看做一项后，也可以用完全平方公式．
【乘法公式】完全平方公式叫做乘法公式，在计算时可以直接使用
例1、将一块边长为a米的正方形广场进行扩建，扩建后的正方形边长比原来长2米，则扩建后广场面积增大了（　　）A．4米2 B．(a2+4)米2 C．(2a+4)米2 D．(4a+4)米2
【分析】(a+2)2-a2=a2+4a+4-a2=4a+4
【完全平方公式的几何背景】
例2、计算：(-3x-4y)2．
(-3x-4y)2=(3x+4y)2=9x2+24xy+16y2
【完全平方公式的直接计算】
把(-3x-4y)看作整体，求其相反数
【分析】互为相反数的两数的平方是相等的
例3、已知(3x+a)2=9x2+bx+4，则b的值为（　　）A．6 B．±6 C．12 D．±12
【利用完全平方公式求参】
【分析】∵(3x+a)2=9x2+bx+4，∴9x2+6ax+a2=9x2+bx+4，∴a2＝4，b＝6a，∴a＝±2，b＝±12．
例4、先化简，再求值：(a+b)2-(a-b)2+5a(a-b)，其中a=3，b=2．
【分析】(a+b)2-(a-b)2+5a(a-b)=a2+2ab+b2-(a2-2ab+b2)+5a2-5ab=4ab+5a2-5ab=5a2-ab，当a=3，b=2时，原式=5×9-3×2=39．
例5、计算：（1）10032； （2）99982
【利用完全平方公式巧算】
【分析】（1）10032=(1000+3)2=10002+2×1000×3+32=1000000+6000+9=1006009
（2）99982=(10000-2)2=100002-2×10000×2+22=100000000-40000+4=99960004
例6、a、b为实数，整式a2+b2-4a+6b的最小值是（　　）A．-13 B．-4 C．-9 D．-5
【完全平方公式的逆用】
【分析】a2+b2-4a+6b=(a2-4a+4)+(a2+6b+9)-13=(a-2)2+(b+3)2-13，∵(a-2)2≥0，(b+3)2≥0，∴(a-2)2+(b+3)2-13的最小值为-13．
例7、计算：(x-y-z)2
【分析】原式=[x+(-y)+(-z)]2=x2+(-y)2+(-z)2+2x(-y)+2(-y)(-z)+2(-z)x=x2+y2+z2-2xy+2yz-2zx
把-y、-z看作整体，则可以用(a+b+c)2=a2+b2+c2+2ab+2bc+2ca这个公式
【完全平方式】对于一个具有若干个简单变元的整式A，如果存在另一个实系数整式B，使A=B2，则称A是完全平方式eg：a2±2ab+b2=(a±b)2，a2±2ab+b2是完全平方式
例8、下列多项式是完全平方式的是（　　）A．a2-ab+b2B．a2-2ab-b2C．2a2+2ab+b2D．a2+4ab+4b2
【分析】a2+4ab+4b2=(a+2b)2
例9、已知关于x的代数式9x2+Mx+1是完全平方式，则M的值为（　　）A．6 B．-6 C．±6 D．不能确定
【完全平方式的相关求参】
【分析】∵关于x的代数式9x2+Mx+1是完全平方式，∴9x2+Mx+1=(3x+1)2=9x2+6x+1，或9x2+Mx+1=(3x+1)2=9x2-6x+1，∴M=±6．
【完全平方式】(a+b)2=a2+2ab+b2(a-b)2=a2-2ab+b2
a2+b2=(a+b)2-2aba2+b2=(a-b)2+2ab
2ab=(a+b)2-(a2+b2)2ab=a2+b2-(a-b)2
2(a2+b2)=(a+b)2+(a-b)2
4ab=(a+b)2-(a-b)2
例10、已知a+b=10，ab=20，则a2+b2的值为（　　）A．80 B．-80 C．60 D．140
a2+b2=(a+b)2-2ab=100-40=60
【分析】a2+b2=(a+b)2-2ab
例11、已知a-b=7，ab=12，那么a2+ab+b2的值是（　　）A．11 B．13 C．37 D．85
∵a-b=7，ab=12，∴a2+ab+b2=(a-b)2+2ab+ab=(a-b)2+3ab=72+3×12=85．
【分析】a2+b2=(a-b)2+2ab
例12、已知(m-n)2=46，(m+n)2=4000，则m2+n2的值为（　　）A．2022B．2023C．3954D．4046
【分析】2(m2+n2)=(m+n)2+(m-n)2
例13、已知x+y=6，xy=5，则(x-y)2的值为（　　）A．25 B．36 C．11 D．16
∵x+y=6，xy=5，∴(x-y)2=(x+y)2-4xy=62-4×5=16．
【分析】4xy=(x+y)2-(x-y)2
【完全平方公式】 (a+b)2=a2+2ab+b2；(a-b)2=a2-2ab+b2 记忆口诀：首平方，末平方，积的两倍在中央（符号随中央）【特征】 ①左边是两个数的和（或差）的平方； ②右边是一个三项式，其中首末两项分别是两数的平方，都为正，中间一 项是两数积的2倍，其符号与左边的运算符号相同．【拓展公式】 (a+b+c)2=a2+b2+c2+2ab+2bc+2ca【注意点】 ①公式中的a、b可是具体数，也可以是单项式或多项式； ②对形如两数和（或差）的平方的计算，都可以用这个公式； ③对于三项的可以把其中的两项看做一项后，也可以用完全平方公式．
【完全平方式】 对于一个具有若干个简单变元的整式A，如果存在另一个实系数整式B，使A=B2，则称A是完全平方式eg：a2±2ab+b2=(a±b)2，a2±2ab+b2是完全平方式
【完全平方式的变形式】 （1）a2+b2=(a+b)2-2ab （2）a2+b2=(a-b)2+2ab （3）2ab=(a+b)2-(a2+b2) （4）2ab=a2+b2-(a-b)2 （5）2(a2+b2)=(a+b)2+(a-b)2 （6）4ab=(a+b)2-(a-b)2