苏科版七年级下册9.5 多项式的因式分解优秀课件ppt

这是一份苏科版七年级下册9.5 多项式的因式分解优秀课件ppt，文件包含苏科版本数学七年级下册95《多项式的因式分解》第3课时课件pptx、苏科版本数学七年级下册95《多项式的因式分解》第4课时课件pptx、苏科版本数学七年级下册95《多项式的因式分解》第5课时课件pptx、苏科版本数学七年级下册952《多项式的因式分解》第2课时原卷版docx、苏科版本数学七年级下册952《整式的因式分解分组分解法与十字相乘法》重难点专项练习七大题型解析版docx等5份课件配套教学资源，其中PPT共80页， 欢迎下载使用。
理解分组分解法的意义，掌握四项式的分组规律
熟练运用分组分解法进行因式分解
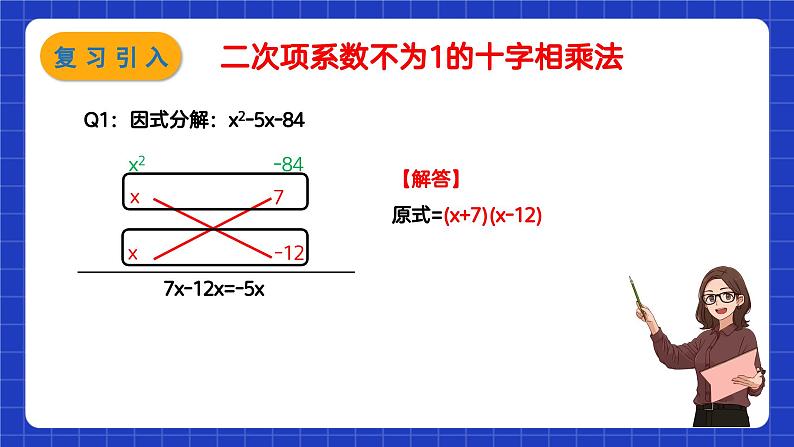
Q1：因式分解（1）x(a+b)+y(a+b)=_________________________；（2）(x-y)2-1=_______________________________.
(x-y+1)(x-y-1)
Q2：下列四项式能否因式分解（1）ax+bx+ay+by； （2）x2-2xy+y2-1.
没有公因式！(灬ꈍ ꈍ灬)
平方差公式——两项完全平方公式——三项but nw——四项
【结论】不能因式分解？
【结论】ax+bx+ay+by与x2-2xy+y2-1能因式分解，只是不能用提公因式法或公式法直接因式分解
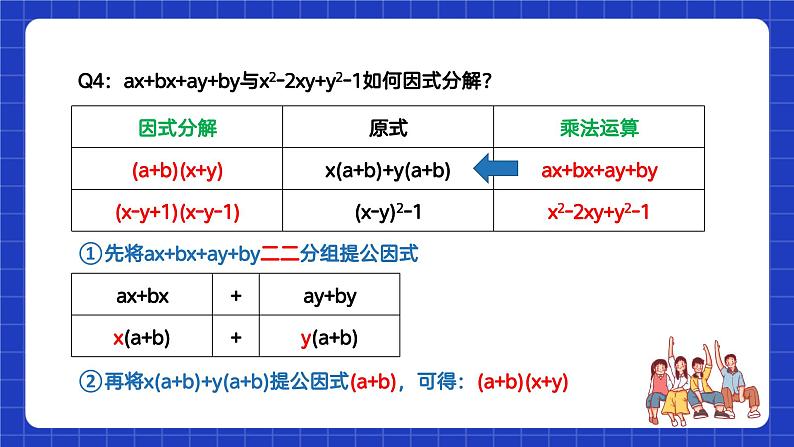
Q4：ax+bx+ay+by与x2-2xy+y2-1如何因式分解？
①先将ax+bx+ay+by二二分组提公因式
②再将x(a+b)+y(a+b)提公因式(a+b)，可得：(a+b)(x+y)
①先将x2-2xy+y2-1三一分组
②再将其中的x2-2xy+y2用完全平方公式分解因式，可得：(x-y)2-1
③最后用平方差公式分解因式，可得：(x-y+1)(x-y-1)
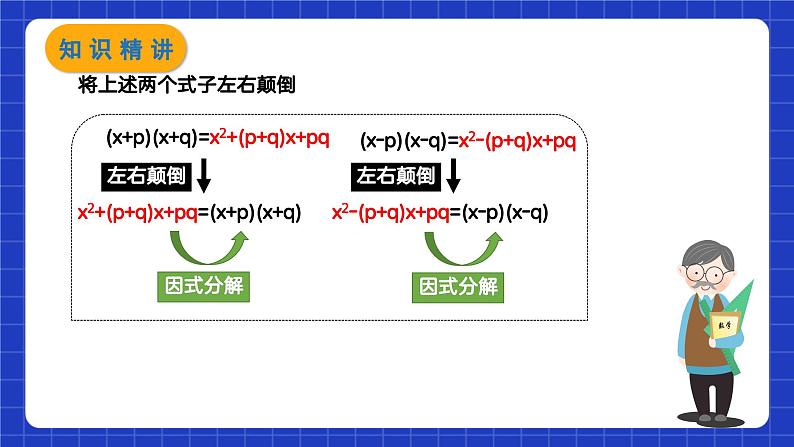
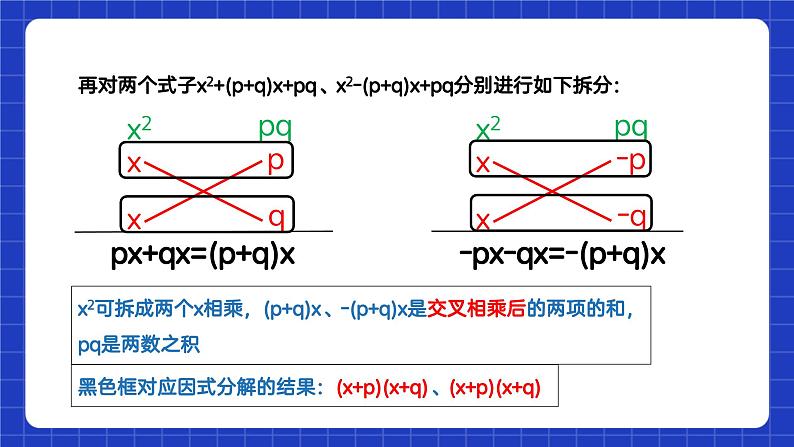
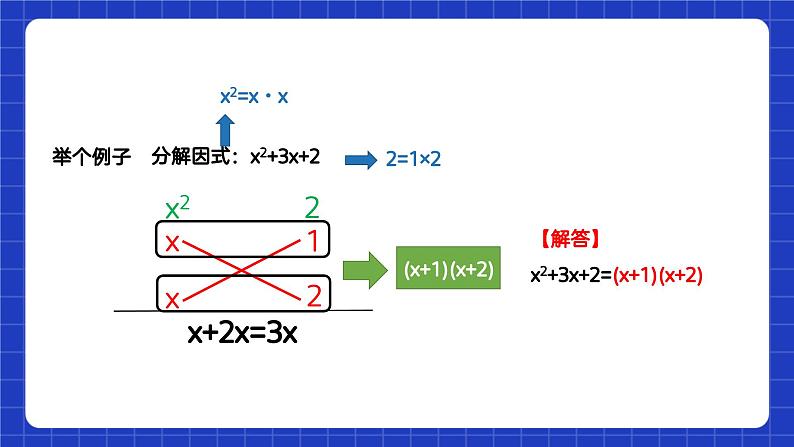
【分组分解法】分组分解法一般是针对四项或四项以上多项式的因式分解，分组有两个目的，一是分组后能出现公因式，二是分组后能运用公式．对于常见的四项式，一般的分组分解有两种形式：①二二分法，②三一分法．
②三一分组：x2-2xy+y2-1=(x2-2xy+y2)-1=(x-y)2-1=(x-y+1)(x-y-1)
eg：①二二分组：ax+ay+bx+by=(ax+bx)+(ay+by)=x(a+b)+y(a+b)=(a+b)(x+y)
【1】因式分解——二二分组：（1）ax-by-bx+ay
【解答】第一步：分组提公因式（选择a、b作为公因式）原式=(ax+ay)-(bx+by)=a(x+y)-b(x+y)第二步：提公因式(x+y)=(x+y)(a-b)
或者第一步：分组提公因式（选择x、y作为公因式）原式=(ax-bx)+(ay-by)=x(a-b)+y(a-b)第二步：提公因式(a-b)=(a-b)(x+y)
【1】因式分解——二二分组：（2）ac2+bd2-ad2-bc2
【解答】第一步：分组提公因式（选择a、b作为公因式）原式=(ac2-ad2)+(bd2-bc2)=a(c2-d2)+b(d2-c2)第二步：提公因式(c2-d2)=a(c2-d2)-b(c2-d2)=(c2-d2)(a-b)
第三步：运用平方差公式=(c+d)(c-d)(a-b)
【1】因式分解——二二分组：（3）(ax+by)2+(ay-bx)2
【解答】第一步：去括号原式=a2x2+2abxy+b2y2+(a2y2-2abxy+b2x2)=a2x2+b2y2+a2y2+b2x2第二步：分组提公因式（选择a2、b2作为公因式）=(a2x2+a2y2)+(b2y2+b2x2)=a2(x2+y2)+b2(x2+y2)
第三步：提公因式(x2+y2)=(x2+y2)(a2+b2)
第二步：分组提公因式，也可以选择x2、y2作为公因式
【1】因式分解——二二分组：（4）9m2-n2+3m-n
【解答】第一步：分组原式=(9m2-n2)+(3m-n)第二步：运用平方差公式=(3m+n)(3m-n)+(3m-n)
第三步：提公因式(3m-n)=(3m-n)(3m+3n+1)
这题没有其他分组方法咯
【1】因式分解——二二分组：（5）16x2-4x-9y2+3y
【解答】第一步：分组原式=(16x2-9y2)-(4x-3y)第二步：运用平方差公式=(4x+3y)(4x-3y)-(4x-3y)
第三步：提公因式(4x-3y)=(4x-3y)(4x+3y-1)
【2】因式分解——三一分组：（1）a2-2ab+b2-4
【解答】第一步：分组原式=(a2-2ab+b2)-4第二步：运用完全平方公式=(a-b)2-4
第三步：运用平方差公式=(a-b+2)(a-b-2)
【2】因式分解——三一分组：（2）1-4x2+4xy-y2
【解答】第一步：分组原式=1-(4x2-4xy+y2)第二步：运用完全平方公式=1-(2x-y)2
第三步：运用平方差公式=(1+2x-y)(1-2x+y)=(2x-y+1)(-2x+y+1)
【2】因式分解——三一分组：（3）y(y-2)-(m-1)(m+1)
【解答】第一步：去括号原式=y2-2y-(m2-1)=y2-2y-m2+1第二步：分组=(y2-2y+1)-m2
第三步：运用完全平方公式=(y-1)2-m2第四步：运用平方差公式=(y-1+m)(y-1-m)=(y+m-1)(y-m-1)
例1、因式分解：4x2-y2-2y-1=__________________．
【因式分解——分组分解法】
(2x+y+1)(2x-y-1)
【分析】原式=4x2-(y2+2y+1)=(2x)2-(y+1)2=(2x+y+1)(2x-y-1)
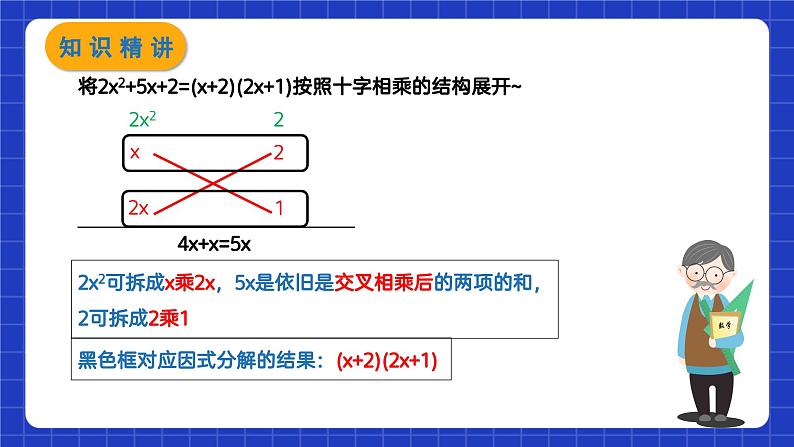
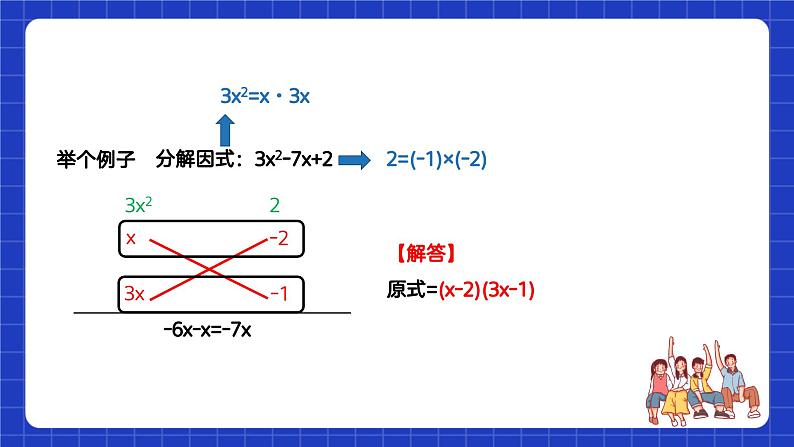
例2、下列分解因式错误的是（　　）A．15a2+5a=5a(3a+1)B．-x2-y2=-(x+y)(x-y)C．ax+x+ay+y=(a+1)(x+y)D．a2-bc-ab+ac=(a-b)(a+c)
【分析】A、15a2+5a=5a(3a+1)，正确；B、-x2-y2=-(x2+y2)，故本选项错误；C、ax+x+ay+y=(ax+x)+(ay+y)=x(a+1)+y(a+1)=(a+1)(x+y)，正确；D、a2-bc-ab+ac=(a2-ab)+(ac-bc)=a(a-b)+c(a-b)=(a-b)(a+c)，正确．
【拓展】因式分解——多项分组：（1）2ax-3bx+x-2a+3b-1
【解答】第一步：分组提公因式（类型：3+3）原式=(2ax-3bx+x)-(2a-3b+1)=x(2a-3b+1)-(2a-3b+1)第二步：提公因式(2a-3b+1)=(2a-3b+1)(x-1)
【拓展】因式分解——多项分组：（2）x3-2x2-x+2+x5-2x4
【解答】第一步：分组提公因式（类型：2+2+2）原式=(x5-2x4)+(x3-2x2)-(x-2)=x4(x-2)+x2(x-2)-(x-2)第二步：提公因式(x-2)=(x-2)(x4+x2-1)
【拓展】因式分解——多项分组：（3）(m-2n)4-2m2-8n2+8mn+1
【解答】第一步：分组提公因式（类型：1+3+1）原式=(m-2n)4-(2m2-8mn+8n2)+1=(m-2n)4-2(m2-4mn+4n2)+1第二步：运用完全平方公式=(m-2n)4-2(m-2n)2+1
第三步：运用完全平方公式again=[(m-2n)2-1]2第四步：运用平方差公式=[(m-2n+1)(m-2n-1)]2=(m-2n+1)2(m-2n-1)2
【拓展】因式分解——多项分组：（4）a2-4b2-c2+a+2b+4bc-c
【解答】第一步：分组原式=a2+a+(2b-c)-(4b2-4bc+c2)第二步：运用完全平方公式=a2+a+(2b-c)-(2b-c)2第三步：分组=[a2-(2b-c)2]+[a+(2b-c)]
第四步：运用平方差公式=(a+2b-c)(a-2b+c)+(a+2b-c)第五步：提公因式(a+2b-c)=(a+2b-c)(a-2b+c+1)
例3、因式分解a2+ab+2ac+bc+c2=________________．
(a+c)(a+b+c)
【分析】原式=(a2+2ac+c2)+(ab+bc)=(a+c)2+b(a+c)=(a+c)(a+c+b)=(a+c)(a+b+c)